控制系统Bode图的模值裕度与相位裕度

对数频率特性曲线即Bode图的两条曲线分别是对数幅频特性与对数相频特性。横坐标均为角频率ω，是按常用对数刻度的，即log ω，其单位是rad/s。对数幅频特性的纵坐标是L（ω）=20log A（ω），是等分刻度的，其单位为dB（即分贝）；而对数相频特性的纵坐标是φ（ω），也是等分刻度的，其单位为角度的（°）或弧度（rad）。

幅（或模）值稳定裕度是开环幅相特性曲线G（jω）与负实轴交点（ω_cg）模值G（ω_cg）的倒数，即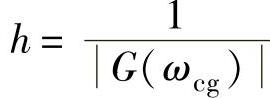；或者是其交点模值倒数的分贝值，即L_h=20log h。

相角稳定裕度是系统开环幅相特性曲线G（jω）上模值等于1的矢量与负实轴的夹角，即γ=φ（ω_c）-（-π）。

提请读者特别关注，MATLAB系统提供的函数命令margin（），不仅能绘制系统开环Bode图，还在Bode图上同时给出计算的系统频域性能指标（剪切频率ω_c、相角稳定裕度γ与-π穿越频率ω_g、幅值稳定裕度L_h）。请看示例。

【例9-4】 单位反馈系统的闭环传递函数为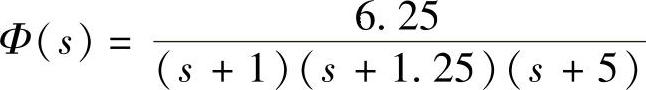，1）试求系统的剪切频率ω_c与相角裕度γ；2）若要求系统具有γ=30°的相角裕度，试计算开环放大倍数应增大的倍数。

解：1）试求系统的剪切频率ω_c与相角裕度γ。

①求系统的开环传递函数与开环增益k。

clear；syms s phi G；phi=6.25/（（s+1）∗（s+1.25）∗（s+5））；

G=factor（phi/（1-phi））；[n，d]=numden（G）；

n=vpa（n/4，3）；d=vpa（factor（vpa（d/4，4）），4）；G=n/d，

程序运行结果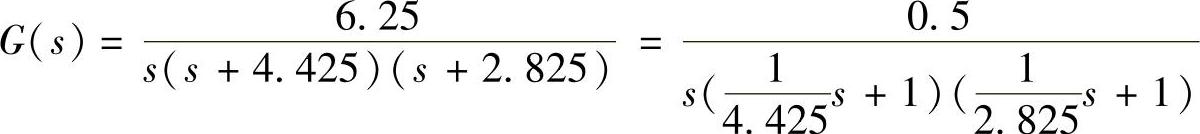

系统开环增益为k=0.5。

②按系统开环传递函数绘制Bode图。

clear；n=0.5；d=conv（conv（[10]，[1/4.4251]），[1/2.8251]）；

s=tf（n，d）；margin（s），

程序运行后绘制系统开环Bode图，如图9-5所示，并算得系统剪切频率ω_c=

0.49rad/s、相角裕度γ=73.9°。

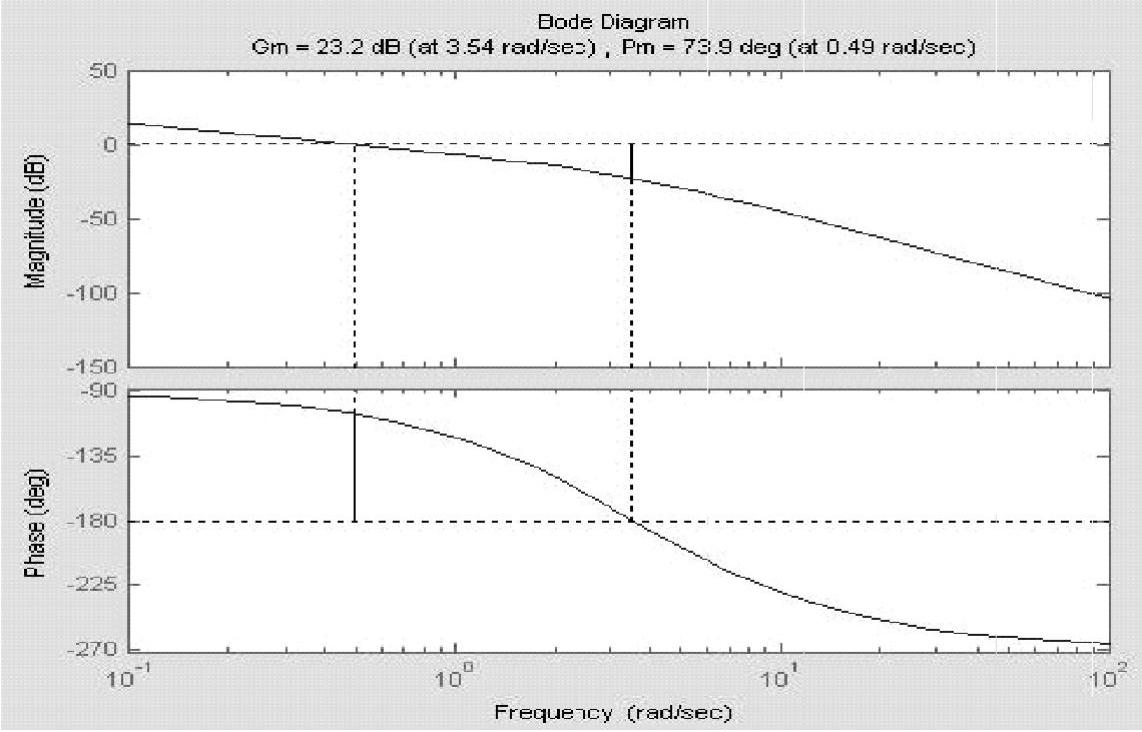
图9-5 系统Bode图

2）若要求系统具有γ=30°的相角裕度，计算开环放大倍数应增大的倍数。由于系统的

φ（ω_c）与系统开环增益无关，即开环放大倍数的变化不影响系统相角裕度，只使开环对数

幅频特性曲线20log|G|上下移动，与横坐标的交点产生变化即ω_c改变。

γ=φ（ω_c）-（-180°）=180°+φ（ω_c）

要γ=30°，则φ（ω_c）=-180°+30°=-150°

φ（ω_c）=-90°-arctan（T₁ω_c）-arctan（T₂ω_c）

clear；syms T1 T2 omegac；T1=1/2.825；T2=1/4.425；

[omegac]=solve（-pi/2-atan（1/2.825∗omegac）-atan（1/4.425∗omegac）=-5/6∗pi，omegac）；

omegac=vpa（omegac，4），

程序运行结果omegac=2.016，即对应系统γ=30°的相角裕度，求得系统剪切频率ω_c2=2.016rad/s。当系统剪切频率ω_c1=0.49rad/s时相角裕度γ=73.9°。

将系统原20log|G|曲线向上移动20log（K）时，其剪切频率由ω_c1=0.49rad/s向右移到ω_c2=2.016rad/s，有、。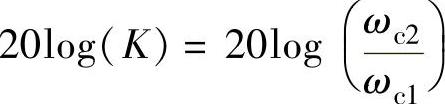

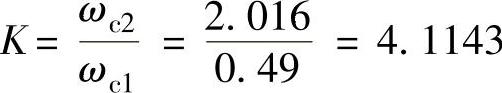即系统开环放大倍数应增大K=4.1143倍。

3）验算γ=30°的相角裕度。

clear；syms xphic gama；T1=1/2.825；T2=1/4.425；wc=2.016；

xphic=（-pi/2-atan（T1∗wc）-atan（T2∗wc））∗180/pi，gama=（180+xphic），

程序运行得到γ=29.9936°≈30°。

【例9-5】 某单位反馈系统的开环传递函数为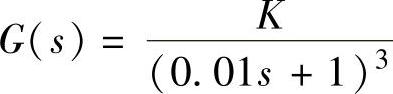。试确定使系统的相角

稳定裕度γ=+45°时的K值。

解：1）确定系统的幅频特性与相频特性。

clear；syms s G phi；syms K omega omegac real；G=K/（（0.01∗s+1）^3）；

G=subs（G，s，j∗omega）；Gabs=abs（G），phi=-3∗atan（0.01∗omega），

程序运行结果

Gabs=1000000/（10000+omega^2）^（3/2）∗abs（K）

phi=-3∗atan（1/100∗omega）

2）确定使系统的相角稳定裕度γ=+45°时的ω_c。

γ=φ（ω_c）-（-180°）

clear；syms omegac gama；gama=pi-3∗atan（0.01∗omegac）；

[omegac]=solve（pi-3∗atan（0.01∗omegac）=pi/4，omegac）；

omegac=vpa（omegac，4），(www.xing528.com)

程序运行结果omegac=100。

3）将ω_c=100代入求系统幅频特性|G（jω_c）|。

clear；syms tau omegac Gabs K；

Gabs=1000000/（10000+omegac^2）^（3/2）∗abs（K）；

Gabs=subs（Gabs，omegac，100），

程序运行结果Gabs=1/400∗20000^（1/2）∗abs（K）。

4）计算K（当ω=ω_c时系统的幅频特性|G（jω_c）|=1或20log|G（jω_c）|=0dB）clear；syms K omegac real；[K]=solve（1/400∗20000^（1/2）∗K=1，K）；K=vpa（K，5），

程序运行结果K=2.8284。

【例9-6】 某单位反馈系统的开环传递函数为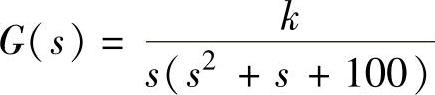。试确定使系统的模稳定裕度L_h=20dB时的k值。系统的开环增益又应取多少？

解：1）确定系统幅频特性与相频特性。

clear；syms s G phi；syms k omega omegac real；

G=k/（s∗（s^2+s+100））；G=subs（G，s，j∗omega）；

Gabs=abs（G），phi=-pi/2-atan（omega/（100-omega^2）），

程序运行结果

Gabs=1/（omega^4-199∗omega^2+10000）^（1/2）∗abs（k/omega）

phi=-1/2∗pi-atan（omega/（100-omega^2））

2）确定ω_g。当ω=ω_g时φ（ω_g）=-180°，对应系统模稳定裕度。

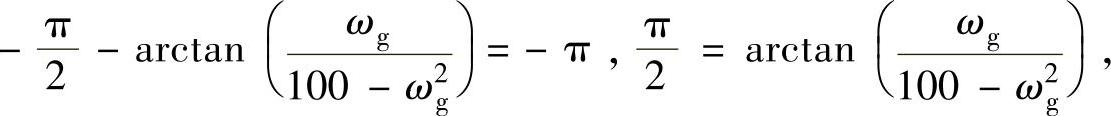
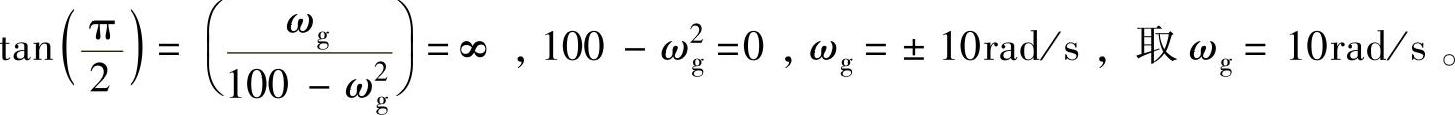
3）将ω_g=10rad/s代入系统幅频特性|G（jω_c）|确定|G（jω_c）|。

clear；syms k omegag Gabs；

Gabs=1/（omegag^4-199∗omegag^2+10000）^（1/2）∗abs（k/omegag）；

Gabs=subs（Gabs，omegag，10），

程序运行结果Gabs=1/1000∗100^（1/2）∗abs（k）。

4）根据题目要求，当ω=ω_g时系统幅频特性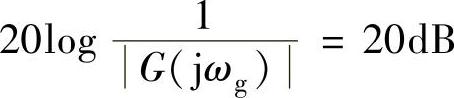，计算k。

clear；syms k omegag real；

[k]=solve（20∗log10（1/（1/1000∗100^（1/2）∗k））=20，k）；k=vpa（k，5），

程序运行后得到k=10。

5）计算系统开环增益K。

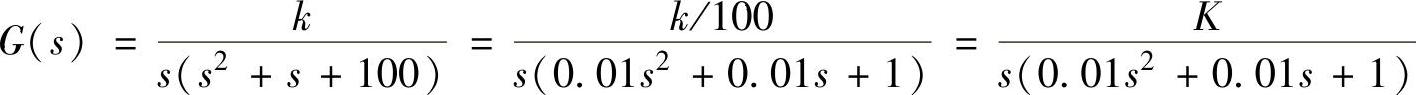
即K=k/100=0.1rad/s。

【例9-7】 某控制系统的开环传递函数为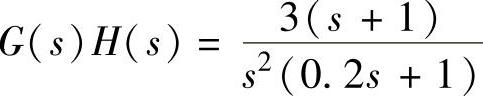，试求系统的频域性能指标ω_c、γ与时域性能指标σ%、t_s。

解：1）求系统的频域性能指标ω_c、γ。

clear；n=3∗[11]；；d=conv（[100]，[0.21]）；GH=tf（n，d）；margin（GH），

运行该程序可得系统的Bode图，如图9-6所示，系统的性能指标如下。

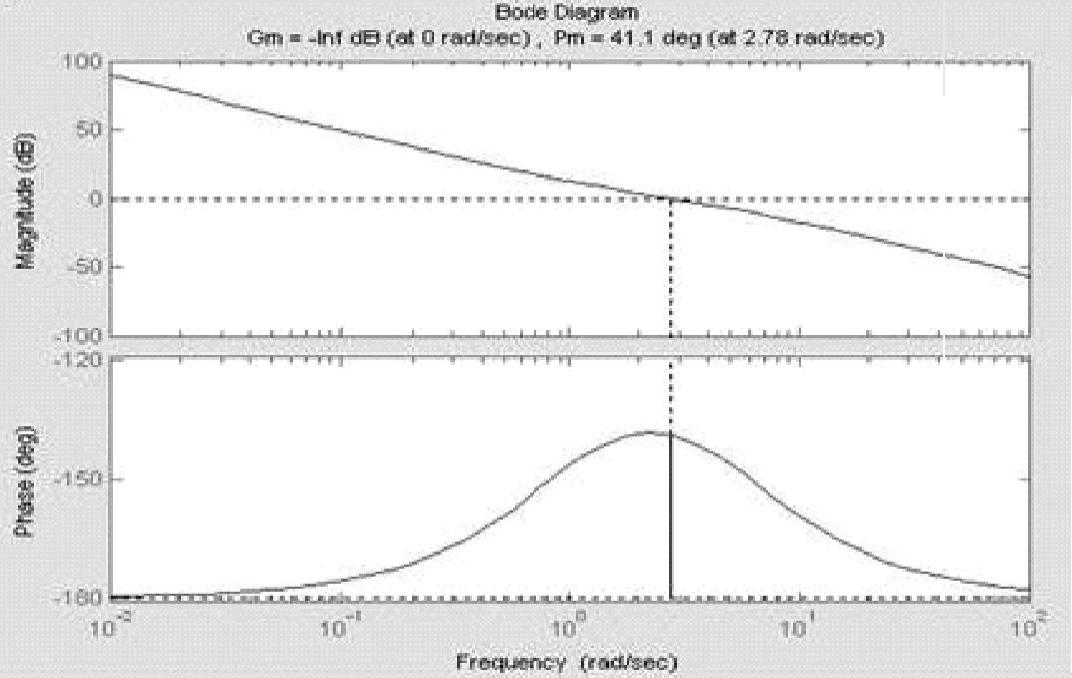
图9-6 系统Bode图

幅值稳定裕度：L_h=∞dB -π穿越频率：ω_g=∞rad/s

相角稳定裕度：γ=41.1° 剪切频率：ω_c=2.78rad/s

2）求系统的闭环传递函数。

clear；syms s n d GH phi；n=3∗（s+1）；d=s^2∗（0.2∗s+1）；GH=n/d；phi=factor（GH/（1+GH）），

程序运行结果。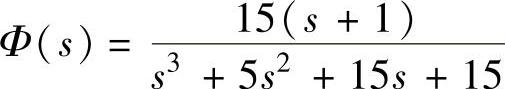

3）求系统的阶跃响应与时域性能指标σ%、t_s。clear；n=15∗[11]；d=[151515]；phi=tf（n，d）；step（phi），grid；[y，t]=step（phi）；perf（1，y，t）；

程序运行后，绘制系统单位阶跃响应曲线，如图9-7所示，并计算出系统时域性能指标σ%=37.2013%，t_s（5%）=1.9071s。

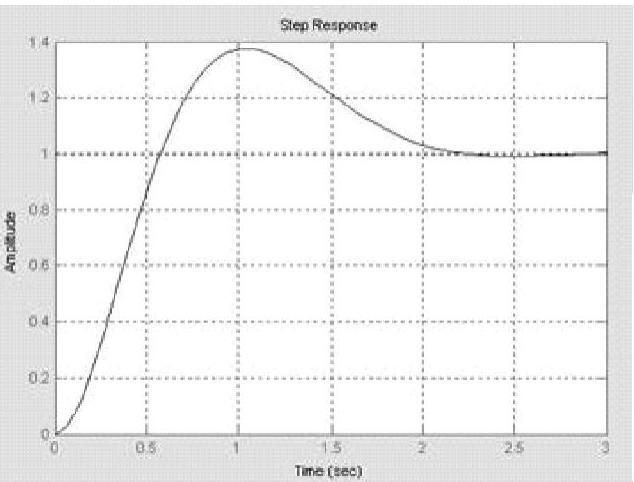
图9-7 系统单位阶跃响应曲线