控制系统频率特性分析

当正弦信号作用于线性系统时，系统稳定后输出的稳态分量仍然是同频率正弦信号，这种过程叫做系统的频率响应。

系统频率响应即系统输出稳态分量与输入正弦信号的复数比叫做系统频率特性，记作：G（jω）=A（ω）e^jφ（ω）。系统频率特性与系统的传递函数之间有着简单而直接的对应关系：G（jω）=G（s）|_s=jω。

【例9-1】 已知系统结构如图9-1所示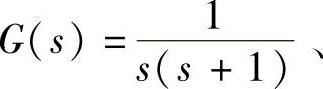，H（s）=1、系统输入r（t）=sin（t），试用MATLAB程序求：1）闭环系统（C/R）频率特性；2）稳态误差（E/R）频率特性；3）稳态输出c（t）与稳态误差e_ser（t）表达式并绘制c（t）与e_ser（t）曲线图。

图9-1 反馈系统结构

解：1）计算闭环系统（C/R）频率特性与稳态输出c（t）并绘制c（t）曲线图。

clear；syms t s omega；G=1/s/（s+1）；H=1；phi=simple（G/（1+G∗H））；phif=subs（phi，s，j∗omega），

r=sin（t）；R=laplace（r）；C=phi∗R；c=ilaplace（C），ezplot（c，[0，10∗pi]），grid；

程序运行后得到闭环系统（C/R）频率特性与稳态输出表达式，并绘制c（t）曲线，如图9-2所示。

2）计算系统稳态误差（E/R）频率特性与稳态误差e_ser（t）并绘制e_ser（t）曲线图。

clear；syms t s omega；G=1/s/（s+1）；H=1；[n，d]=numden（1/（1+G∗H））；phier=n/d；

phierf=simple（subs（phier，s，j∗omega）），r=sin（t）；R=laplace（r）；

Essr=phier∗R；essr=ilaplace（Essr），ezplot（essr，[0，13∗pi]），grid；

程序运行后得到稳态误差（E/R）频率特性与稳态误差表达式并绘制e_ser（t）曲线，如图9-3所示。需要提请读者注意的是，本题解算程序采用符号运算，与此相对应要采用符号运算的绘图函数命令ezplot（）。

图9-2 系统稳态输出c（t）曲线

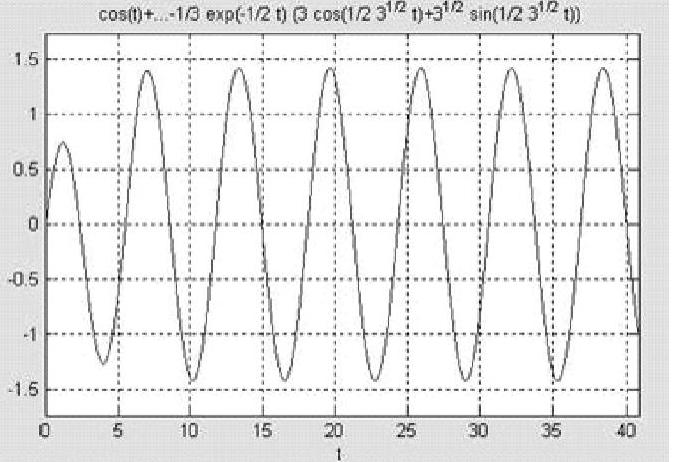
图9-3 系统稳态误差e_ser（t）曲线

【例9-2】 设二阶系统具有以下开环传递函数。试求1）系统开环频率特性；2）相角裕度γ与阻尼比ζ之间的关系式。

解：1）求开环频率特性的模。

clear；syms s GH GHabs zet omega omegan real；

GH=omegan^2/（s∗（s+2∗zet∗omegan））；

GH=subs（GH，s，j∗omega），GHabs=abs（GH），

程序运行结果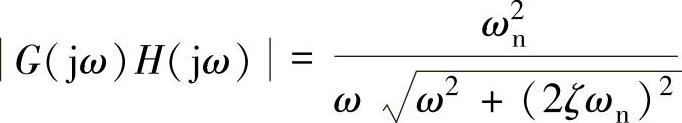，还有系统开环频率特性

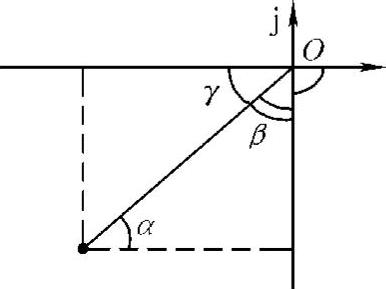
演算结果说明频率响应复数的实部与虚部都是负值，幅角在第3象限，如图9-4所示。

2）当ω=ω_c时|G（jω_c）|=1，求ω_c=f（ζ，ω_n）。

clear；syms zet omegac omegan real；

[omegac]=solve（omegan^2/（4∗zet^2∗omegan^2+omegac^2）^（1/2）/omegac=1，omegac），

程序运行结果

omegac=

（-2∗zet^2+（4∗zet^4+1）^（1/2））^（1/2）∗omegan

-（-2∗zet^2+（4∗zet^4+1）^（1/2））^（1/2）∗omegan

i∗（2∗zet^2+（4∗zet^4+1）^（1/2））^（1/2）∗omegan

-i∗（2∗zet^2+（4∗zet^4+1）^（1/2））^（1/2）∗omegan

(https://www.xing528.com)

图9-4 复数表达式的图示

取。

3）频率响应复数表达式图9-4的角度关系。

。

当ω=ω_c时，。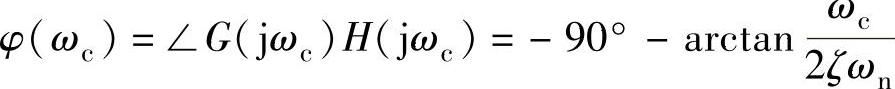

根据自动控制原理，相角裕度的定义γ=φ（ω_c）-（-π），图9-4中γ为相角裕度，由图可知γ=180°-∠G（jω_c）H（jω_c）。

4）求相角裕度γ与阻尼比ζ之间的关系式。

已经求得。

clear；syms s GH GHang gama；syms zet omegac omegan real；

omegac=（-2∗zet^2+（4∗zet^4+1）^（1/2））^（1/2）∗omegan；

GHangc=-pi/2-atan（omegac/（2∗zet∗omegan）），

程序运行结果φ（ω_c）=∠G（jω_c）H（jω_c）=-90°-β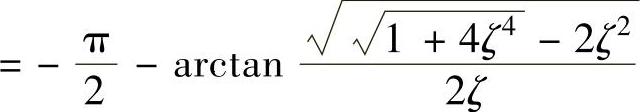即，根据直角三角形里两锐角的关系tan β=cotα，由图9-4可知α=γ，故得到。

【例9-3】 已知单位负反馈系统开环传递函数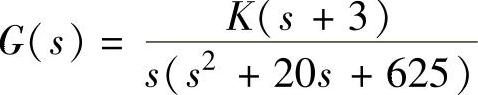，试计算剪切频率ω_c分别为1）15rad/s、2）50rad/s时的相位角∠G（jω_c）与相角裕度γ。

解：1）振荡环节的频率特性与相频特性。

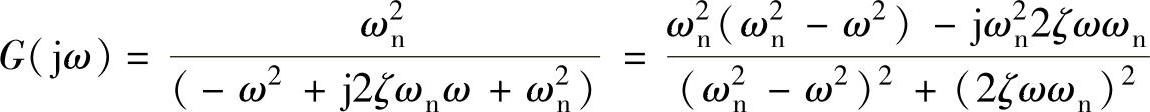
当ω_n>ω时，频率特性G（jω）实部为正、虚部为负，相角在第4象限，即

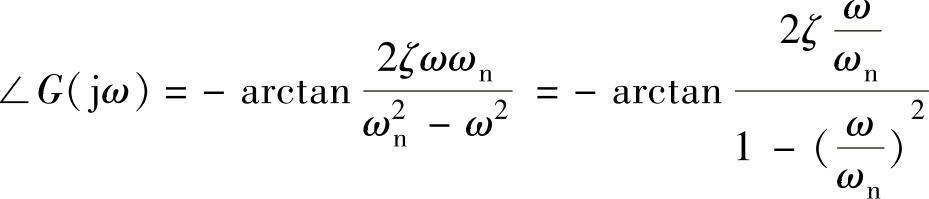
当ω_n<ω时，频率特性G（jω）实部为负、虚部也为负，相角在第3象限，即

2）系统相频特性与增益无关。

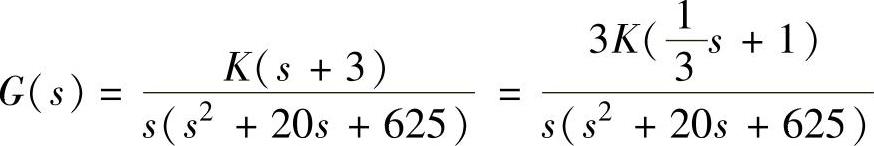
3）计算ω_n与ζ。

clear；syms omeqan zeta；

[zeta，omegan]=solve（omegan^2=625，2∗zeta∗omegan=20），

程序运行后得到ω_n=25rad/s、ζ=2/5。

4）当ω_c=15rad/s时求∠G（jω_c）与γ。

clear；syms w wn；T1=1/3；wn=25；zeta=2/5；wc=15；

angG=atan（T1∗w）-pi/2-atan（（2∗zeta∗w/wn）/（1-w∗w/wn/wn））；

angG=subs（angG，w，wc）∗180/pi，gama=（180+angG），

程序运行后得到∠G（jω_c）=-48.1798°、γ=131.8202°。

5）当ω_c=50rad/s时求∠G（jω_c）与γ。

clear；syms w wn；T1=1/3；wn=25；zeta=2/5；wc=50；

angG=atan（T1∗w）-pi/2-atan（（2∗zeta∗w/wn）/（1-w∗w/wn/wn））-pi；

angG=subs（angG，w，wc）∗180/pi，gama=（180+angG），

程序运行后得到∠G（jω_c）=-155.3611°、γ=24.6389°。