根轨迹设计工具优化方案

低于MATLAB 7.5版本的系统，其工具箱里有一个系统根轨迹分析与设计工具Rltool，只要在MATLAB命令窗口里输入“rltool”然后按Enter键，就得到一个系统根轨迹分析的图形界面。升级到MATLAB 7.5版本，这个工具有很大改进，增加了许多功能。虽然进入工具的操作仍然是在MATLAB命令窗口里输入“rltool”然后按Enter键，但此后操作情况与老版本的就很不同。工具的名称改为“SISO Design for SISO Design Task”，即单输入单输出设计工具。

需要说明的是，MATLAB 7.5版本的这个设计工具，界面多、功能多，但互相重复，给人有条理欠清晰之感。建议读者先看懂以下示例，并学会按下例自己解题即可。在此基础上，读者可再对其中其他功能逐步接触、深入了解并掌握。

【例8-6】 已知系统开环传递函数为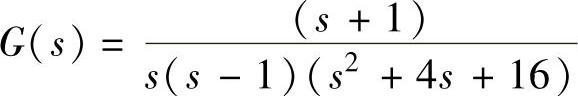，试用根轨迹设计器查看在K=31时闭环系统单位阶跃给定响应曲线、Bode图、给定单位冲激响应曲线；要求系统单位阶跃给定响应一次微弱超调σ%<20%后即衰减，试设计零极点校正器。

解：1）绘制未处理系统开环根轨迹图。

clear；n=[11]；d=conv（conv（[10]，[1-1]），[1416]）；

sys=tf（n，d）；rlocus（sys），

程序运行后得到未处理系统根轨迹图，如图8-14所示。图8-14中显示了5个点的相关数据，从中可以看出，随着开环增益的增加，根轨迹变化趋势符合根轨迹法则。

2）绘制未处理系统闭环阶跃响应曲线。

clear；n1=[11]；d1=conv（conv（[10]，[1-1]），[1416]）；

s1=tf（n1，d1）；sys=feedback（s1，1）；step（sys），grid；

程序运行后得到未处理系统阶跃响应曲线如图8-15所示，曲线发散、系统不稳定。

3）在程序文件方式下执行程序，即必须编写以下调用rltool（）函数的程序并且命名，在MATLAB命令窗口里输入该程序名后按Enter键。若在Notebook方式下执行，无法进入设计工具。

% MATLAB PROGRAM sx2L0806.m

clear；n1=[11]；d1=conv（conv（[10]，[1-1]），[1416]）；

s1=tf（n1，d1）；rltool（s1），

图8-14 未处理系统开环根轨迹图

程序运行后，首先给出图8-16所示的设计工具加载提示

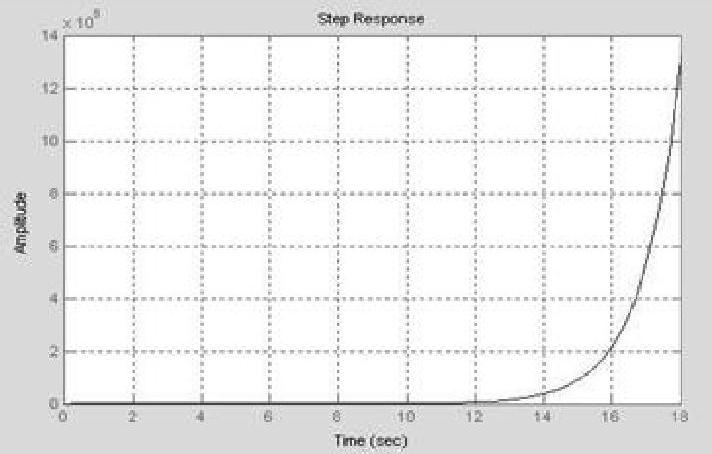
图8-15 未处理系统闭环阶跃响应曲线

图8-16 设计工具加载提示

加载完后，计算机显示器同时弹出已有本系统信息的“SISO Design for SISO Design Task”单输入单输出设计工具（见图8-17）与“Control and Estimation Tools Manager”控制与估计工具管理器（其系统结构卡“Architecture”处于打开状态，见图8-18）。

4）验证是否含有本系统信息的“SISO Design for SISO Design Task”设计工具。

在图8-17所示设计工具中，选择菜单【Analysis】中的【Response to Step Command】命令，执行后得到与图8-15所示同样的原系统单位阶跃响应。由图可知，阶跃响应发散，系统不能工作，必须对系统进行处理。

5）控制与估计工具管理器（Control and Estimation Tools Manager）简介。

在图8-18右边上方，有5张重叠卡：“Architecture”系统结构卡、“Compensator Editor”补偿器编辑卡、“Graphical Tuning”图形调试卡、“Analysis Plots”图形分析卡、“Automated Tuning”自动调试卡。(www.xing528.com)

在5张卡下是“Current Architecture”系统通用结构图。

在通用结构图下是4个按钮：控制结构图按钮“Control Architecture”、回环型式按钮“Loop Configuration”、系统数据按钮“System Data”、采样时间转换按钮“Sample Time Conversion”。

图8-17 单输入单输出设计工具中的根轨迹

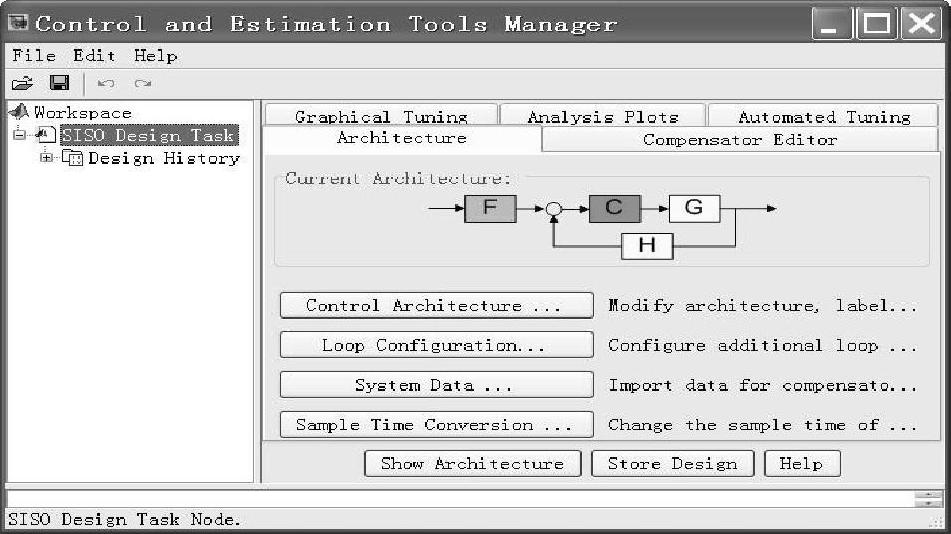
图8-18 控制与估计工具管理器

最下部还有3个按钮：“Show Architecture”显示结构图按钮、“Store Design”存储设计按钮、“Help”帮助按钮。

6）进入控制与估计工具管理器进行设计。

当选择“Compensator Editor”补偿器编辑卡时，即会弹出补偿校正器编辑器对话框，如图8-19所示。在“Pole/Zero”卡下的“Dynamics”区内任何地方单击鼠标右键，即弹出【Add Pole/Zero】菜单，选择【Complex Zero】，在右部“Edit Selected Dynamics”区域下方的“Real Part”右边空白框内输入零点实部（-3）、在“Imaginary Part”右边空白框内输入零点虚部（3.6），再在“Dynamics”下的数据区内单击确认数据输入，即得到一对共轭复数零点（-3±3.6i），如图8-20所示。不需设计极点，还需要输入控制器C的增益Gain=296后，最后单击按钮【Store Design】存储设计（见图8-20）并且确认（见图8-21）。

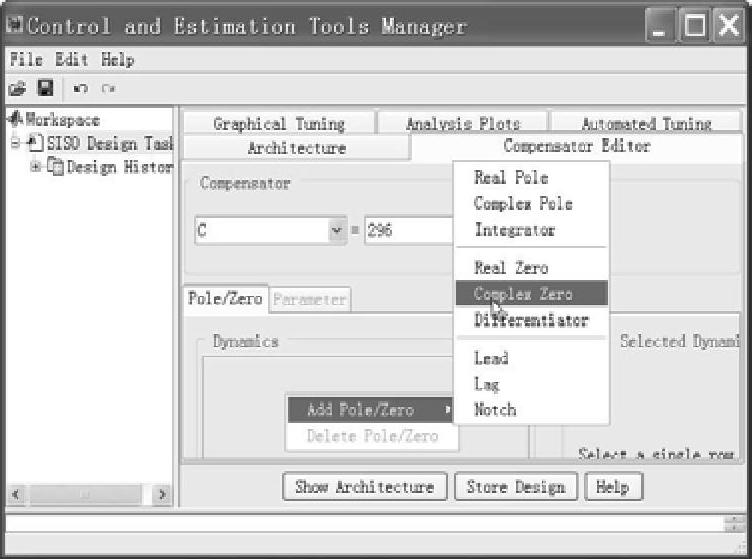
图8-19 补偿校正器编辑器对话框

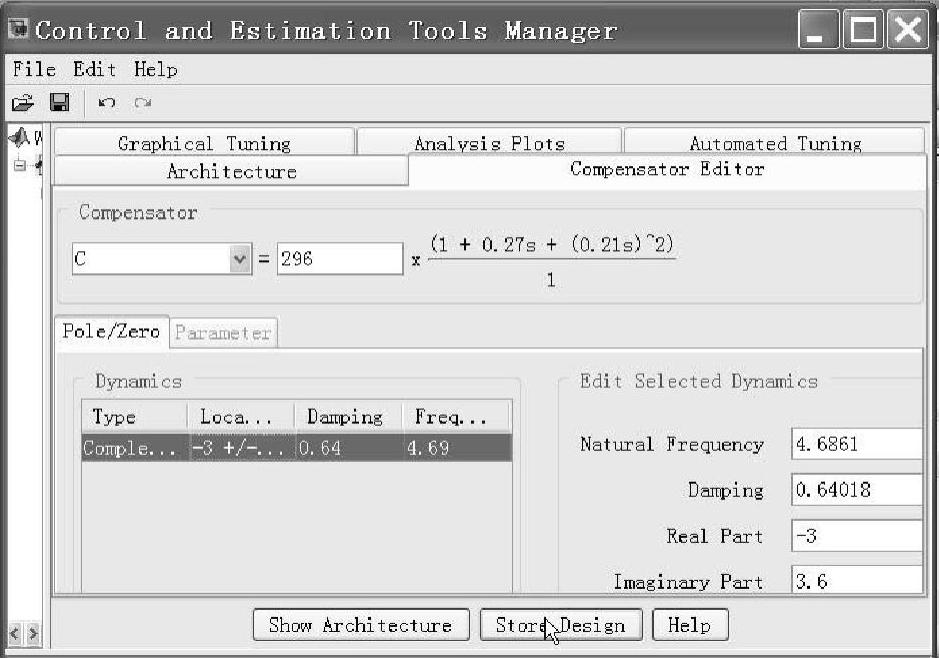
图8-20 输入数据后的补偿校正器编辑器对话框

图8-21 确认存储设计

此时图8-17变成图8-22。再在图8-22中选择菜单【Analysis】中的【Response to Step Command】命令，原系统发散的阶跃响应则变为图8-23所示曲线。由图可知，系统不仅稳定，曲线非常理想，调节时间短（0.6s左右），超调小（17%左右），并且超调后一次衰减至终了值不振荡，即阶跃响应有优良的性能指标。

运行以下MATLAB程序，也可绘制同图8-23所示的单位阶跃响应曲线。

clear；gn=[11]；gd=conv（conv（[10]，[1-1]），[1416]）；G=tf（gn，gd）；

cn=296∗[0.21∗0.210.271]；cd=[1]；C=tf（cn，cd）；CG=C∗G；F=1；

sys=feedback（CG，F）；t1=0：0.0001：4；step（sys，t1），grid；key=1；

[y，t]=step（sys）；[sigma，tp，ts]=perf（key，y，t）；

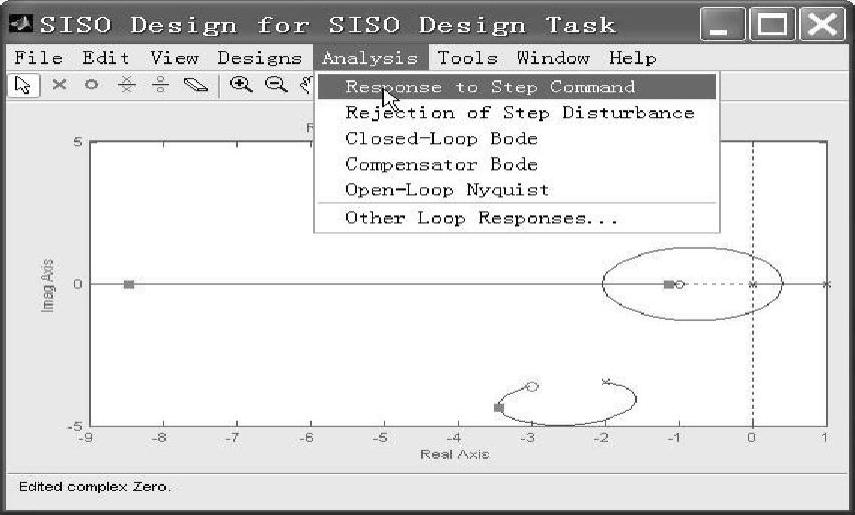
图8-22 设计后系统根轨迹图

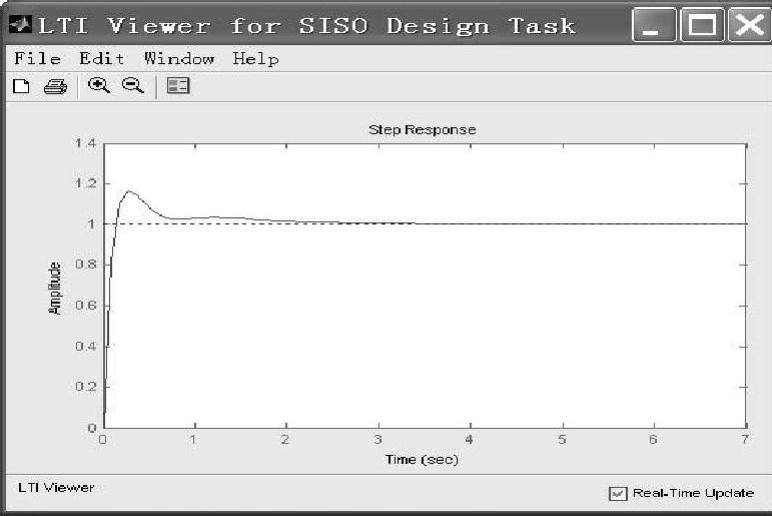
图8-23 性能指标优良的单位阶跃响应曲线