稳态误差计算在扰动输入下的影响

控制系统在扰动输入作用下的稳态误差计算只能使用Laplace变换的终值定理。

【例7-9】 已知r（t）=1（t），n（t）=0.1·1（t）且指定e（t）=r（t）-c（t）。试求图7-7所示系统总的稳态误差。

解：1）对系统判稳。

系统闭环特征方程：D（s）=0.5s²+s+200=0。有a_i>0，有D₂=a₁a₂-a₀a₃=1×200-0.5×0=200>0，根据Lienard-Chipard判据，系统闭环稳定。

2）仅在r（t）作用下（n（t）=0），求e_ssr的公式。

图7-7 负反馈控制系统

对本系统有，E_r（s）=R（s）-C_r（s），

其稳态误差为。

3）仅在r（t）=1（t）作用下求e_ssr。

clear；syms G1 G2 H r R Cr Er t s essr；G2=200/（s∗（0.5∗s+1））；G1=1；H=1；

r=sym（Heaviside（t））；R=laplace（r）；

[n，d]=numden（G1∗G2/（1+G1∗G2∗H））；phi=n/d；(www.xing528.com)

Cr=phi∗R；Er=simple（R-Cr）；essr=limit（s∗Er，s，0，right），

程序运行后得到e_ssr=0。

4）仅在n（t）作用下（r（t）=0），求e_ssn的公式。

对本系统有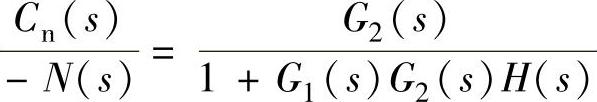，E_n（s）=R（s）-C_n（s），其稳态误差为。

5）仅在n（t）=0.1·1（t）作用下，求e_ssn。

clear；syms G1 G2 H r R n N Cr Er t s essn；

G1=1；G2=200/（s∗（0.5∗s+1））；H=1；R=0；

n=sym（-0.1∗Heaviside（t））；N=laplace（n）；

[num，den]=numden（G2/（1+G1∗G2∗H））；phin=num/den；

Cn=phin∗（-N）；En=simple（R-Cn）；

essn=limit（s∗En，s，0，right）；essn=vpa（essn，2），

程序运行后得到e_ssn=-0.1。那么e_ss=e_ssr+e_ssn=0-0.1=-0.1。