在系统输出端定义误差，即误差=系统输出量的希望值-输出量实际值。必须对《控制系统MATLAB计算及仿真》中的相关概念与关系式认真复习与深入理解。
【例7-8】 一反馈系统前向通道传递函数G（s）=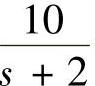
与反馈通道传递函数H（s）=1，系统输入r（t）=1（t）时，试计算系统输出端的稳态位置误差ess
。当G（s）=
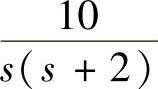而H（s）=1+10s与r（t）=t×1（t）时，再计算系统输出端的稳态位置误差e
ss。
解：1）对系统判稳。
①G（s）=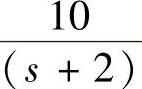
与H（s）=1时。
clear；syms s G H GH R C phier essrp；G=10/（s+2）；H=1；GH=G∗H；
phier=1/（1+GH）；[n，d]=numden（phier），
程序运行结果n=s+2、d=s+12，即闭环特征根为-12，故系统闭环稳定。
②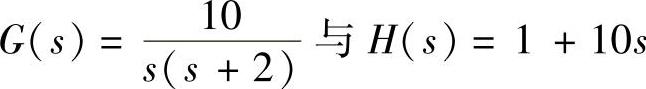
时。
clear；syms s G H GH R C phier essrp；G=10/（s∗（s+2））；
H=1+10∗s；GH=G∗H；phier=1/（1+GH）；[n，d]=numden（phier），(https://www.xing528.com)
程序运行结果n=s∗（s+2）、d=s^2+102∗s+10。
检查闭环特征根的正负。
clear；p=[110210]；roots（p），
程序运行后得知两个特征根均为负，故系统闭环稳定。
2）当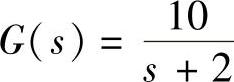
与H（s）=1以及输入r（t）=1（t），计算控制系统输出端稳态误差。clear；syms s；G=10/（s+2）；H=1；r=sym（
1∗1（t）
）；[essrp]=osteerr（G，H，r）；
程序运行后得到系统输出端的稳态位置误差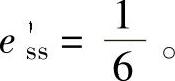
3）当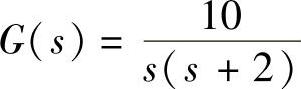
与H（s）=1+10s以及输入r（t）=t×1（t），计算系统输出端稳态误差。
clear；syms s；G=10/（s∗（s+2））；H=1+10∗s；；r=sym（
t∗1（t）
）；[essrp]=osteerr（G，H，r）；
程序运行后得到系统输出端的稳态位置误差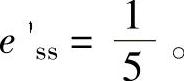
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
