控制系统误差系数的静态和动态特性分析

计算控制系统静态误差系数与动态误差系数是系统稳态误差计算的基础，用MATLAB程序解算会简捷、高效而精准。

【例7-1】 已知两个单位负反馈系统的闭环传递函数分别为1）与2）。试求两系统的稳态位置、速度与加速度误差系数K_p、K_v与K_a。

解：1）对系统a判稳。

clear；P=[1237]；roots（P），

语句执行结果

ans=-2.1325

0.0662+1.8106i

0.0662-1.8106i

根据代数判据，有一对共轭复根实部为正，系统a不稳定，故不能定义稳态误差系数。

2）系统b的计算。

①对系统b判稳。

clear；P=[5210]；roots（P），

语句执行结果

ans=-0.2000+1.4000i

-0.2000-1.4000i

即系统的特征根均有负实部，根据代数稳定判据，系统b稳定。

②计算系统b的开环传递函数。

clear；syms s G；

[G]=solve（（1+G）∗（3∗s+10）=G∗（5∗s^2+2∗s+10），G）；

G=factor（G）；G=collect（G，s），

程序运行后得到开环传递函数

③计算系统b的稳态位置、速度与加速度误差系数。

clear；syms s；G=（3∗s+10）/s/（-1+5∗s）；

H=1；[Kp，Kv，Ka]=Kpva（G，H）；

程序执行后得到系统b的静态位置误差系数K_p=∞、静态速度误差系数K_v=-10与静态加速度误差系数K_a=0。

【例7-2】 已知系统结构图如图7-1所示。试求局部反馈加入前后系统的静态位置、速度与加速度误差系数K_p、K_v与K_a。

解：1）局部反馈加入前。

①求系统传递函数。

clear；syms s G1 G2 H2 G phi1 phi；

G1=（2∗s+1）/s；G2=10/（s∗（s+1））；H2=0；

phi1=G2/（1+G2∗H2）；G=factor（G1∗phi1），

phi=factor（G/（1+G）），

程序执行后得到。

图7-1 系统结构图

②对系统判稳。

clear；P=[112010]；roots（P），程序执行后得到3个根的实部全是负的，根据代数稳定判据，系统稳定。③计算系统的稳态位置、速度与加速度误差系数。

clear；syms s；G=10∗（2∗s+1）/s^2/（s+1）；H=1；[Kp，Kv，Ka]=Kpva（G，H）；　程序执行后得到系统静态位置误差系数K_p=∞、静态速度误差系数K_v=∞与静态加速

度误差系数K_a=10。必须说明，求s→0极限的Kpva.m中，必须指明right即从右趋向于0，否则计算出错。2）局部反馈加入后。①求系统的传递函数。

clear；syms s G1 G2 H2 G phi1 phi；

G1=（2∗s+1）/s；G2=10/（s∗（s+1））；H2=2；

phi1=G2/（1+G2∗H2）；G=factor（G1∗phi1），

phi=factor（G/（1+G）），程序执行后得到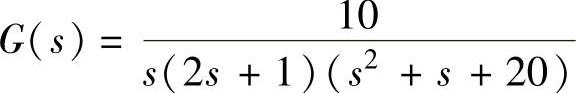、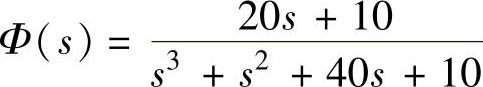。②对系统判稳。

clear；P=[114010]；roots（P），程序执行后得到3个根的实部全是负的，根据代数稳定判据，系统稳定。③计算系统的稳态位置、速度与加速度误差系数。

clear；syms s；G=10/s∗（2∗s+1）/（s^2+s+20）；H=1；

[Kp，Kv，Ka]=Kpva（G，H）；(www.xing528.com)

程序执行后得到系统静态位置误差系数K_p=∞、静态速度误差系数K_v=1/2与静态加速度误差系数K_a=0。

【例7-3】 设单位负反馈系统前向通道传递函数为，已知输入信号为

r（t）=sin（ω₀t），试求系统的动态误差系数C₀～C₅，并用动态误差系数求稳态误差e_ss。

解：1）求系统的动态误差系数C₀～C₅。

clear；syms s；G=100/（s∗（0.1∗s+1））；H=1；dyerr（G，H）；

语句执行结果

ans=1/100∗s+9/10000∗s^2-19/1000000∗s^3-71/100000000∗s^4+261/10000000000∗s^5

即C₀=0，C₁=1×10^-2，C₂=9×10^-4，C₃=-19×10^-6，C₄=-71×10^-8，C₅=261×10^-10。

2）求系统的稳态误差e_ss。

clear；syms w0 t r ess C1 C2 C3 C4 C5；

r=sin（w0∗t）；r1=diff（r，t）；r2=diff（r，t，2）；

r3=diff（r，t，3）；r4=diff（r，t，4）；r5=diff（r，t，5）；

C0=0；C1=1/100；C2=9/10000；C3=-19/1000000；C4=-71/100000000；

C5=261/10000000000；es=vpa（C0∗r+C1∗r1+C2∗r2+C3∗r3+C4∗r4+C5∗r5，4）；

ess=collect（collect（es，cos（w0∗t）），sin（w0∗t）），

程序执行结果

ess=

（-.9000e-3∗w0^2-.7100e-6∗w0^4）∗sin（w0∗t）+（.1000e-1∗w0+.1900e-4∗w0^3+.2610e-7∗w0^5）∗cos（w0∗t）

即

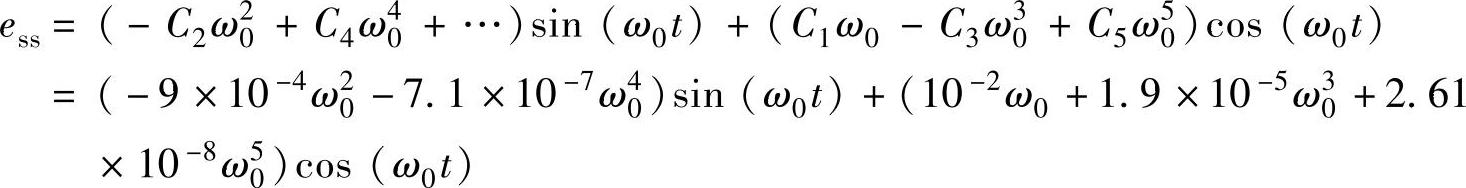
【例7-4】 两系统结构分别如图7-2与图7-3所示。当输入信号为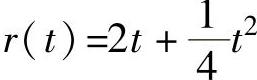时，若要求4min内系统的稳态误差不超过6m，应选用哪个系统？

图7-2 控制系统a

图7-3 控制系统b

解：1）若采用静态误差系数法，图7-2与图7-3均为Ⅰ型系统，在作用下稳态误差均为∞。为求得系统静态误差随时间的变化规律，需要用动态误差系数法。

2）求图7-2所示系统的动态误差系数C₀～C₅。

clear；syms s；G=1/s/（s+1）；H=1；dyerr（G，H）；

程序运行结果ans=s-s^3+s^4，即C₀=0、C₁=1、C₂=0、C₃=-1、C₄=1、C₅=0。

3）求图7-2所示系统a的稳态误差e_ssa。

clear；syms C0 C1 C2 C3 t s r rp rpp rppp ess；

C0=0；C1=1；C2=0；C3=-1；r=2∗t+t^2/4；rp=diff（r，t）；

rpp=diff（r，t，2）；rppp=diff（r，t，3）；

ess=C0∗r+C1∗rp+C2∗rpp+C3∗rppp；

essa=subs（ess，t，4），

程序运行后得到当t=4min时，e_ssa=4m。

4）求图7-3所示系统b的动态误差系数C₀～C₅。

clear；syms s；G=1/s/（10∗s+1）；H=1；dyerr（G，H）；

程序运行结果ans=s+9∗s^2-19∗s^3-71∗s^4+261∗s^5，即C₀=0、C₁=1、C₂=9、C₃=-19、C₄=-71、C₅=261。

5）求图7-3所示系统的稳态误差e_ssb。

clear；syms C0 C1 C2 C3 t s r rp rpp rppp ess；C0=0；C1=1；C2=9；C3=-19；

r=2∗t+t^2/4；rp=diff（r，t）；rpp=diff（r，t，2）；rppp=diff（r，t，3）；

ess=C0∗r+C1∗rp+C2∗rpp+C3∗rppp；essb=subs（ess，t，4），

程序运行结果是当t=4min时，e_ssb=8.5 m。

6）结论：当t=4min时，e_ssa=4 m<6m，所以应该选用系统a。