利用Bode图法判断系统稳定性的方法

有了系统的Bode图，就可以计算频域性能指标。从控制原理上说，当计算出的相角稳定裕度γ>0时，系统闭环稳定，否则不稳定。

在第9章中将要介绍的求系统模值裕度与相角裕度的MATLAB函数margin（），既可绘制系统Bode图，又能够计算频域性能指标。函数命令调用格式为

margin（sys）

[Gm，Pm，Wcg，Wcp]=margin（sys）

当不带输出参数引用函数时，margin（）函数可在当前图形窗口中绘制出带有稳定裕度的Bode图。输入参数sys一般是用系统开环传递函数描述的系统模型，输出参数返回的Gm或L_h是系统模值裕度及其对应的-π穿越角频率Wcg或ω_g、Pm或γ是相角裕度及其对应的剪切角频率Wcp或ω_c。对于开环SISO系统，既可以是连续时间系统，也可以是离散时间系统。请看示例。

【例6-7】 已知某系统开环传递函数为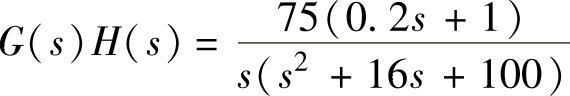，试用Bode图法判断

闭环系统的稳定性，并绘制阶跃响应曲线予以验证。

解：1）用Bode图对闭环系统判稳。

clear；num=75∗[000.21]；den=conv（[10]，[116100]）；[Gm，Pm，Wcg，Wcp]=bod（num，den）；

程序运行后绘制系统Bode图，如图6-8所示，并计算出频域指标：模值稳定裕度Gm或L_h=∞dB；-π穿越频率Wcg或ω_g=∞rad/s；相角稳定裕度Pm或γ=91.6644°；剪切频率Wcp或ω_c=0.7573rad/s。这些数据说明系统闭环不仅稳定，而且有很好的稳定裕度。

2）绘制系统单位阶跃响应曲线验证系统的稳定性。

clear；num=75∗[000.21]；den=conv（[10]，[116100]）；key=1；stepp（key，num，den）；

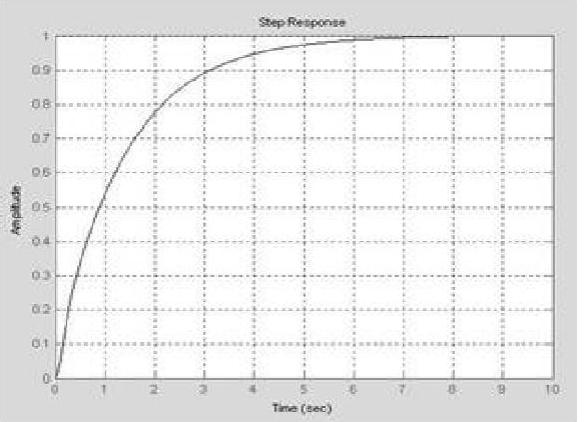
程序运行后，绘制出系统的单位阶跃响应曲线，如图6-9所示。闭环系统的响应曲线表明，系统不仅稳定，而且单位阶跃响应不超调，并有良好的性能指标。

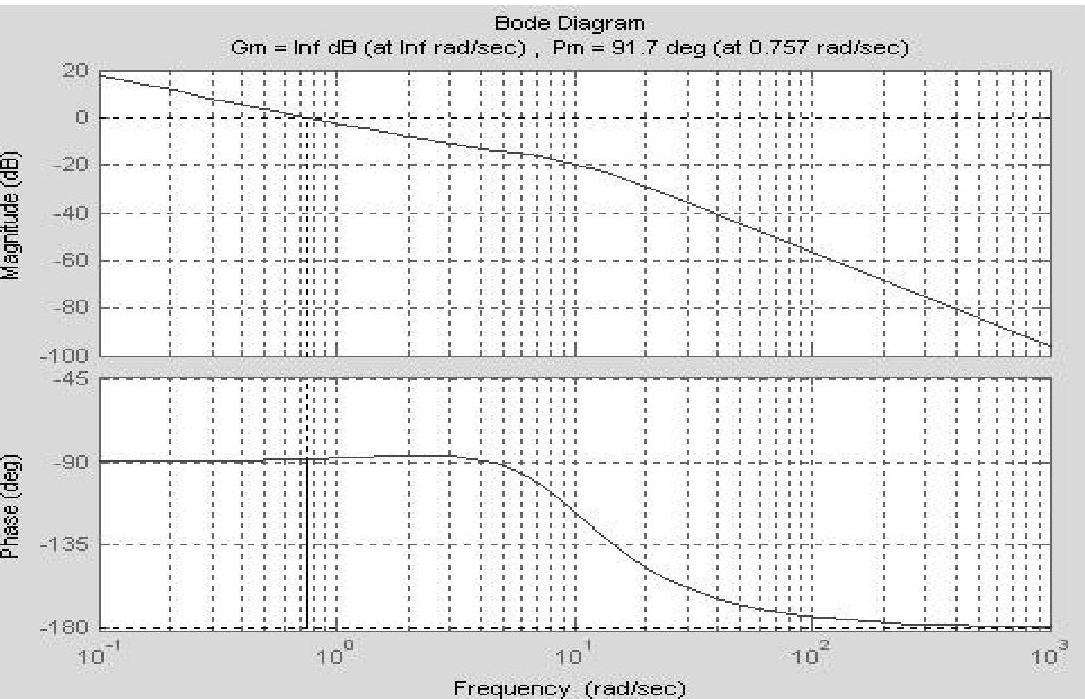
图6-8 系统Bode图

(www.xing528.com)

图6-9 系统单位阶跃响应曲线

还可绘制系统仿真模型并借助模型（sx2L0607.mdl）验证以上单位阶跃响应是正确的。

【例6-8】 已知某系统开环传递函数为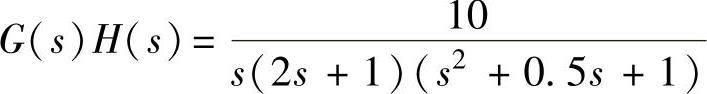，试用Bode图法判断闭环系统的稳定性，并用阶跃响应曲线验证。

解：1）用Bode图对闭环系统判稳。

clear；num=[0010]；den=conv（conv（[10]，[21]），[10.51]）；[Gm，Pm，Wcg，Wcp]=bod（num，den）；

程序运行后绘制出系统的Bode图，如图6-10所示，并计算出系统频域性能指标：模值稳定裕度L_h=20log 0.075=-22.4988dB；相角稳定裕度γ=-136.3866°；-π穿越频率ω_g=0.7067rad/s；剪切频率ω_c=1.6210rad/s。指标模值稳定裕度与相角稳定裕度均为负值，数据说明系统闭环是不稳定的。

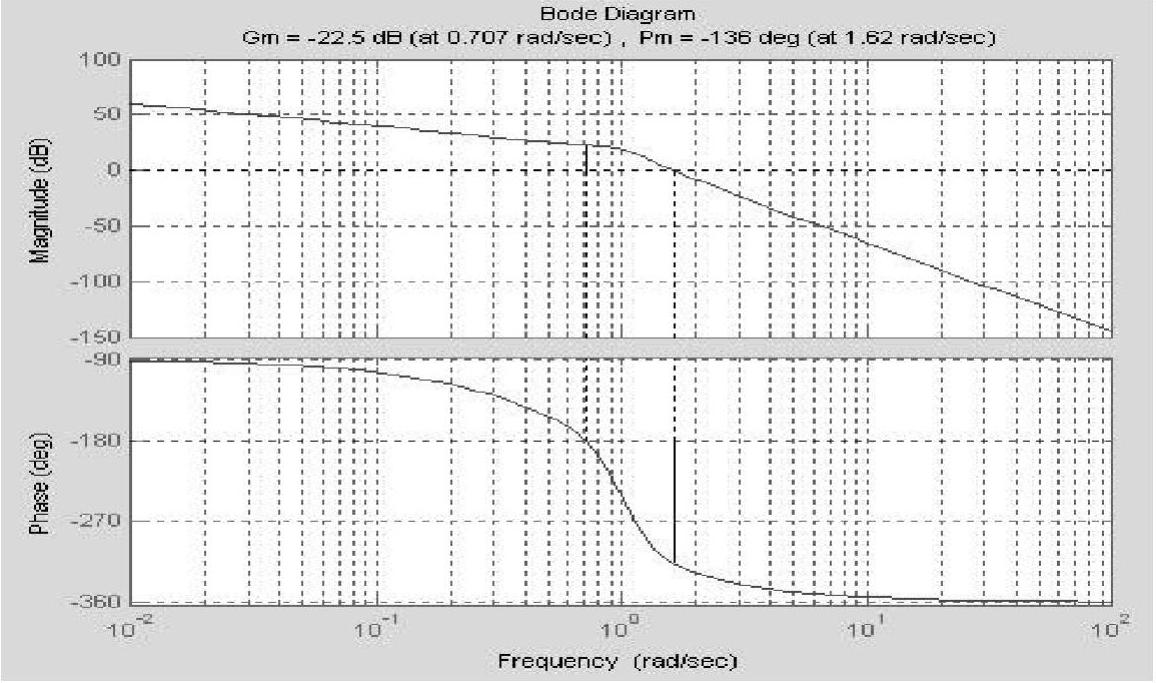
图6-10 系统Bode图

2）绘制系统仿真模型sx2L0608.mdl（见图6-11）与单位阶跃响应曲线验证系统的稳定性。

clear；[a，b，c，d]=linmod2（sx2L0608）；sys=ss（a，b，c，d）；t1=0：0.001：10；step（sys，t1），grid；

程序运行后，绘制出系统的单位阶跃响应曲线，如图6-12所示，闭环系统的单位阶跃响应是发散的振荡，表明系统不稳定，验证了用Bode图判定系统不稳定的结论。

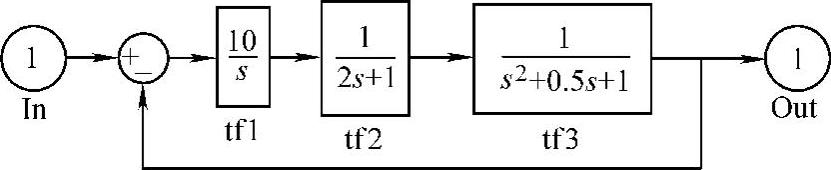
图6-11 系统仿真模型sx2L0608.mdl

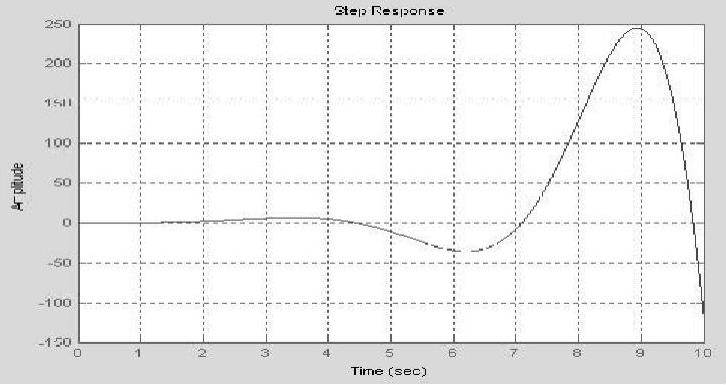
图6-12 系统的单位阶跃响应曲线