MATLAB实现根轨迹法判定系统稳定性

根轨迹是开环系统中某个参数变动（0→∞）时闭环特征根在s平面上移动的轨迹。只要根轨迹在s平面纵坐标的左侧，对应的系统闭环就是稳定的。一旦根轨迹与s平面纵坐标相交或穿越纵坐标到其右侧，对应系统闭环就不稳定。

根轨迹分析的MATLAB实现将随后复习，本节先用其中的一个绘制系统零极点图的函数pzmap（）。函数命令调用格式为

[p，z]=pzmap（sys）

pzmap（p，z）

第一种格式的输入变量sys是LTI对象。当不带输出变量引用时，pzmap（）函数可在当前图形窗口中绘出系统的零极点图。在图中，极点用“×”表示，零点用“○”表示。当带有输出变量引用函数时，可返回系统零极点位置的数据，而不直接绘制零极点图。零点数据保存在变量z中，极点保存在变量p中。如果需要可以再用pzmap（p，z）绘制零极点图。

需要说明的是，如果对象sys是系统开环传递函数，pzmap（p，z）绘制的就是系统开环的零极点图。如果对象sys是闭环传递函数，pzmap（p，z）绘制的就是闭环系统的零极点图。

另外，两个MATLAB函数是用来绘制根轨迹图的rlocus（）与计算给定一组根的系统根轨迹增益与其相应的极点的rlocfind（）（参见根轨迹分析的MATLAB实现），本章解题都要用到。

【例6-5】 设一系统开环传递函数为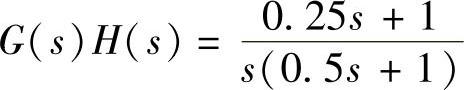。1）试绘制该系统闭环零极点图，并对系统判稳。2）当系统开环传递函数为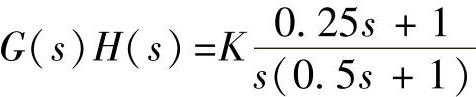时，试绘制该系统常规根轨迹图，并对系统判稳。

解：1）绘制系统闭环零极点图并对系统判稳。clear；num=[0.251]；den=[0.510]；[p，z]=pzmapp（num，den）；

程序运行后绘制系统闭环零极点图如图6-3所示，在图上单击极点“×”与零点“○”，就会出现三个文本框，计算机直接标出该点的“Zero”（零点坐标）、该点的“Pole”（极点坐标）、对应系统的“Dmping”（阻尼系数）、“Overshoot”（超调量）、“Frequency”（无阻尼自然振荡角频率）等参数。还计算出系统闭环极点p₁=-1.25+j0.6614、p₂=-1.25-j0.6614，闭环零点z=-4，计算数据与图示数据两者一致，都表明闭环系统是稳定的。

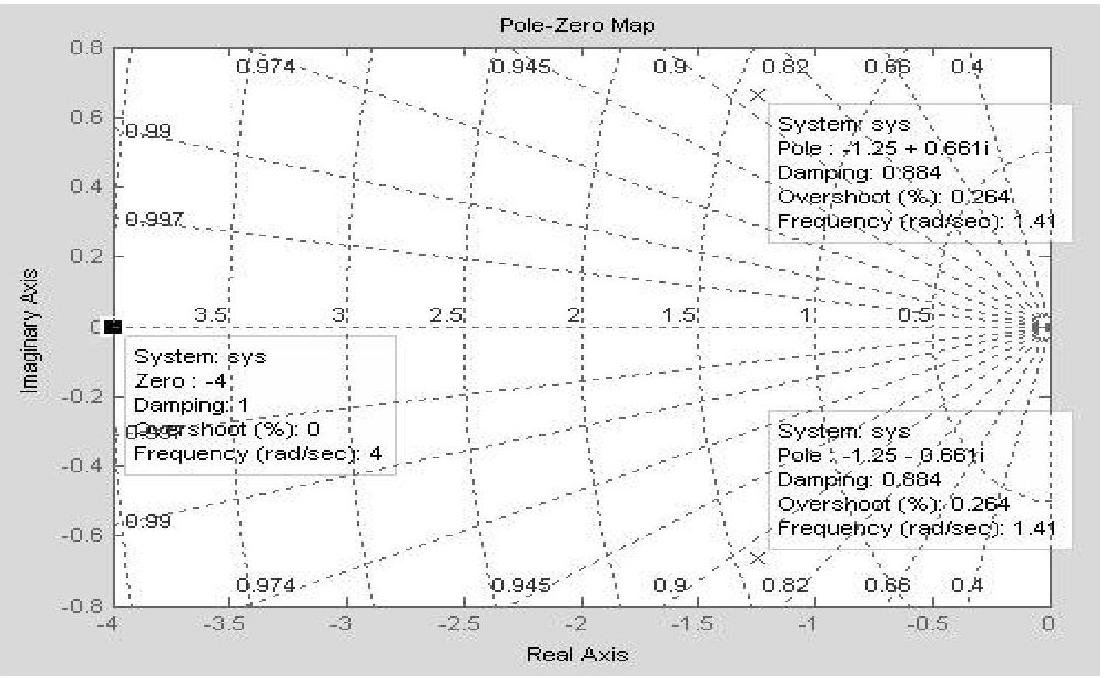
图6-3 系统闭环零极点图

2）当系统的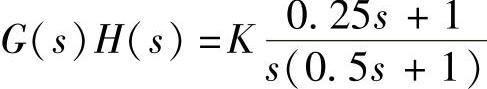，绘制该系统根轨迹图并对系统判稳。clear；num=[0.251]；den=conv（[10]，[0.51]）；key=1；rlocuss（key，num，den）；

程序运行后绘制系统根轨迹图，如图6-4所示。单击根轨迹图上某一点，也会出现一个文本框，计算机直接标出该点的“Gain”（K值）、该点“Pole”（坐标）、对应系统的“Dmping”（阻尼系数）、“Overshoot”（超调量）、“Frequency”（无阻尼自然振荡角频率）等参数（见图6-4）。而且在同一根轨迹图上，可用光标多次单击图上的不同点，显示不同点的参数。由于光标指点的不确定性，显示器显示的数据有误差。

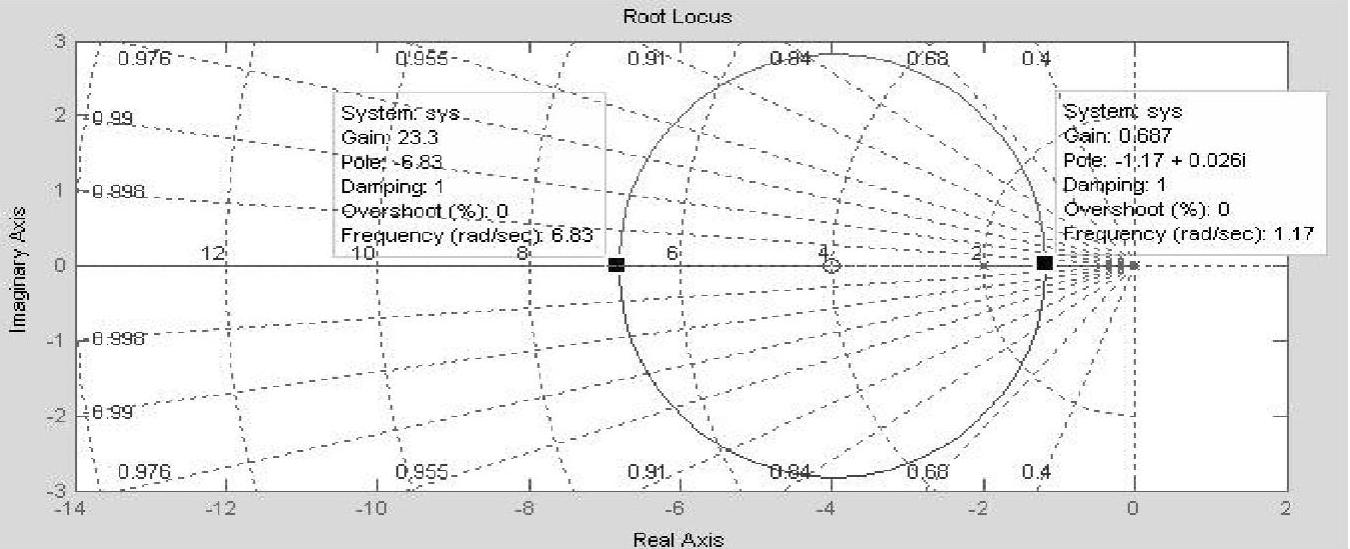
图6-4 系统根轨迹图

该系统根轨迹起始于两个开环极点：p₁=0与p₂=-2，在横轴上根轨迹相对而行，经汇合点d₁=-1.172又分离成两半圆，在横轴上汇合点d₂=-6.828又分离，一支根轨迹指向开环零点z₁=-4，另一支指向-∞。当参数K（0→∞）变动时，根轨迹均在s平面纵坐标的左侧，对应的系统闭环总是稳定的。

读者还可以运行以上key=2时的程序，程序中有一条带鼠标操作的函数命令rlocfind（）。带左端输出的函数命令执行后，可在图形窗口根轨迹图中显示十字形光标，当选择根轨迹上某一点（即十字形光标指向根轨迹上该点）时，其相应的增益由变量k记录，与此增益相关的所有极点记录在变量polse中。从显示所有极点的数值（即位置），就可判断系统的稳定性。

按以上叙述对根轨迹图进行两次操作（可多次操作），得两个分离点：d₁=-1.172、d₂=-6.828，对应着开环增益K₁=0.686、K₂=23.31。

当在根轨迹实轴上第一区段即自系统开环极点p₁=0、p₂=-2指向分离点d₁=-1.172的区段时，对应的0≤K≤0.686；当在实轴上第二区段即自分离点d₂=-6.828指向开环零点z₁=-4与无穷远时，对应的23.31≤K≤∞。这都对应着系统闭环阶跃响应无超调。

当在根轨迹圆上时，系统闭环特征方程出现共轭复根，意味着系统闭环阶跃响应有超调，但系统闭环还是稳定的。

【例6-6】 设一系统开环传递函数为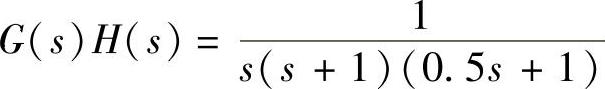，1）试绘制该系统闭环零极点图，并对系统判稳。2）当系统开环传递函数为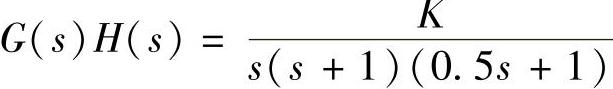时，试绘制该系统的常规根轨迹图，再对系统判稳并用阶跃响应曲线验证。

解：本题解法同上题。

1）绘制系统闭环零极点图并对系统判稳。clear；num=[1]；den=conv（conv（[10]，[11]），[0.51]）；[p，z]=pzmapp（num，den）；

程序运行后得到系统闭环极点为p₁=-2.5214、p_2.3=-0.2393±0.8579j，闭环零点为空即没有闭环零点。程序运行后绘制该系统闭环的零极点图，如图6-5所示，计算数据与图示两者一致，即闭环极点都在s平面纵坐标的左侧，表明闭环系统是稳定的。(www.xing528.com)

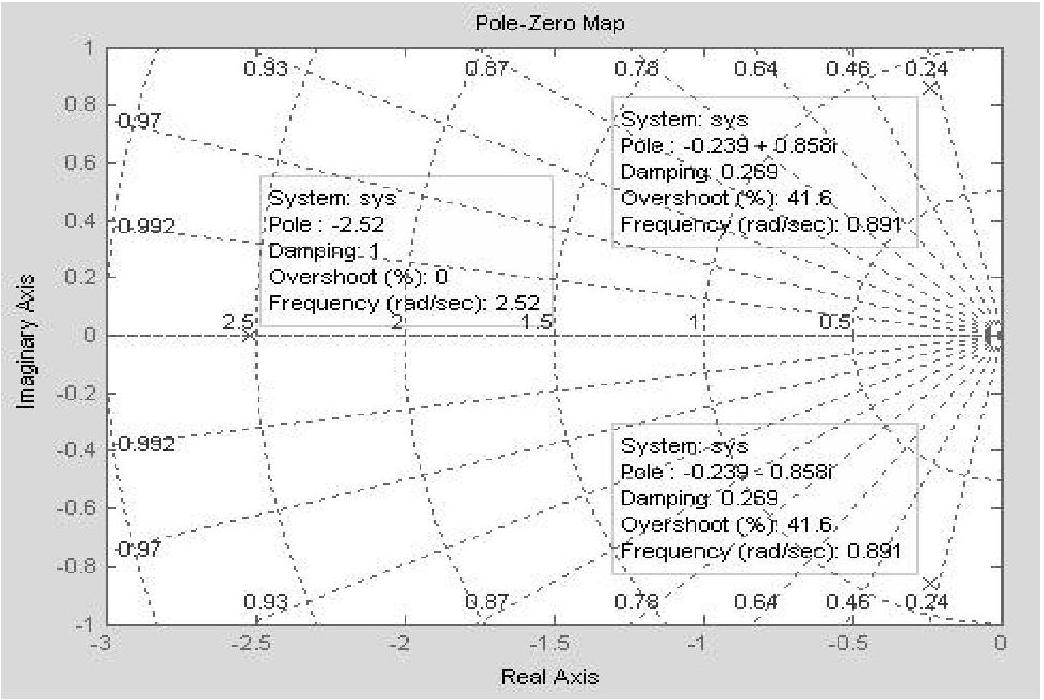
图6-5 系统闭环零极点图

2）系统的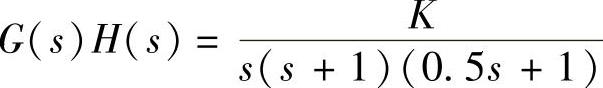绘制该系统根轨迹图并对系统判稳。

clear；num=[1]；den=conv（[110]，[0.51]）；key=1；rlocuss（key，num，den）；

程序运行后绘制系统根轨迹图，如图6-6所示。再单击根轨迹图上的4个点，出现4个文本框（见图6-6）。由于光标指点的不确定性，显示器显示的数据有误差。

读者也可以运行以上key=2时的程序，当选择根轨迹图上的点为（-6）时，实际鼠标指点为（-6.0296-0.0155i），对应的k=61.1035，此时系统3个极点为p₁=-6.0296、p_2.3=1.5148±j4.2395。

在此提一个问题：如何验证以上数据对本系统是正确的？

图6-6 系统根轨迹图

当参数K（0→3）变动时，根轨迹均在s平面纵坐标的左侧，对应的系统闭环是稳定的。一旦根轨迹穿越纵坐标到达其右侧，对应的K>3，那么系统闭环就不稳定。

当在根轨迹实轴上的区段时，对应着系统闭环阶跃响应无超调，系统闭环稳定。当不在根轨迹实轴上的区段时，系统闭环特征方程出现了共轭复根，意味着系统闭环阶跃响应有超调，但系统闭环还是稳定的。

3）当系统的K=1.2、K=3与K=4时，用程序绘制系统闭环单位阶跃响应曲线。

clear；t=0：0.01：30；

n1=[1]；d1=conv（conv（[10]，[11]），[0.51]）；

n=1.2∗n1；s1=tf（n，d1）；sys=feedback（s1，1）；

figure（1）；step（sys，t）；grid；pause；

n=3∗n1；s1=tf（n，d1）；sys=feedback（s1，1）；

figure（2）；step（sys，t）；grid；pause；

n=4∗n1；s1=tf（n，d1）；sys=feedback（s1，1）；

figure（3）；step（sys，t）；grid；

程序运行后，绘制出系统的K=1.2、K=3与K=4时，单位阶跃响应曲线如图6-7所示。由图6-7a可见，当K=1.2时，系统单位阶跃响应曲线为衰减的振荡；当K=3时即图6-7b，系统的单位阶跃响应曲线为等幅振荡，对应着系统临界稳定；当K=4时即图6-7c，系统的单位阶跃响应曲线为发散的振荡，对应着系统不稳定。这完全验证了以上运算的结论。

图6-7 系统单位阶跃响应曲线

在此再提一个问题：如何分别绘制系统K=1.2、K=3与K=4时的系统仿真模型（sx2L0606a.mdl、sx2L0606b.mdl、sx2L0606c.mdl）并借助仿真模型验证以上单位阶跃响应是正确的？