Lienard-Chipard稳定判据判定系统稳定性

可以用另一种判据——Lienard-Chipard稳定判据判定系统稳定性。其判据是：对于线性定常系统的特征方程D（s）=a₀sⁿ+a₁s^n-1+…+a_n-1s+a_n=0（a₀>0），系统稳定的必要且充分条件是：特征方程的各项系数均大于0，且Hurwitz行列式中奇数阶子行列式（即D₁，D₃，D₅…）或偶数阶子行列式（即D₂，D₄，D₆…）大于0。

需要指出的是，Hurwitz行列式在《控制系统MATLAB计算及仿真》Hurwitz稳定判据中已经说明。

【例6-2】 试确定图6-1所示系统参数τ取何值能使系统稳定。

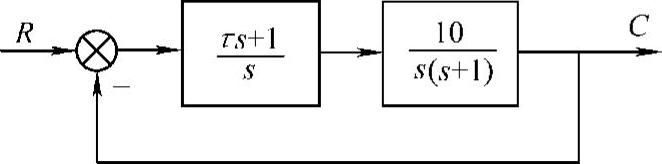
图6-1 三阶系统结构图

解：1）求系统闭环特征式。

clear；syms s tau G1 G2 G D n d phi；

G1=（tau∗s+1）/s；G2=10/（s∗（s+1））；G=G1∗G2；

phi=factor（G/（1+G））；[n，d]=numden（phi）；D=d，

程序运行结果D=s^3+s^2+10∗tau∗s+10。

2）用Lienard-Chipard判据判定系统稳定性。要系统稳定，首先特征方程各项系数均应大于0，系数a₀=1、a₁=1、a₂=10τ、a₃=10。所以a₂=10τ>0，即τ>0。

其次，因系统最高阶次n=3，则可计算Hurwitz行列式中偶数阶子行列式（即D₂）应大于0。用程序计算二阶子行列式。

clear；syms a1 a2 a3 a0 tau D2；a0=1；a1=1；

a2=10∗tau；a3=10；A=[a1 a3；a0 a2]；D2=det（A），

程序运行后得到D2=10∗tau-10，即要系统稳定，必须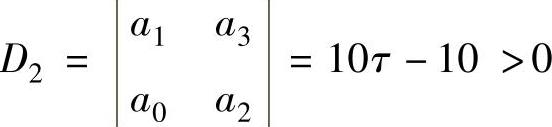，所以τ>1。综合结果为τ>1。

【例6-3】 设控制系统的开环传递函数为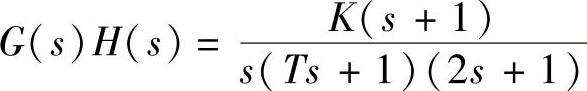，试确定使闭环系统稳定的K与T的取值范围。

解：1）求系统闭环特征式。

clear；syms s K T GH D n d phi；GH=K∗（s+1）/（s∗（T∗s+1）∗（2∗s+1））；

phi=factor（GH/（1+GH））；[n，d]=numden（phi）；D=d；D=collect（D，s^2），程序运行结果D=2∗T∗s^3+（2+T）∗s^2+（K+1）∗s+K。

2）用Lienard-Chipard稳定判据判定系统稳定性。

因a₀=2T、a₁=2+T、a₂=K+1、a₃=K，故a₀=2T>0，T>0；a₁=2+T>0，T>-2；a₂=K+1>0，K>-1；a₃=K>0，K>0。

用程序计算二阶子行列式：(www.xing528.com)

clear；syms a1 a2 a3 a0 K T D2；a0=2∗T；a1=2+T；a2=K+1；a3=K；

A=[a1 a3；a0 a2]；D2=det（A）；D2=collect（D2，K），

程序运行结果D2=（2-T）∗K+2+T，系统要稳定，需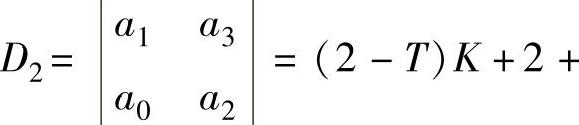T>0，所以2+T>（T-2）K，即0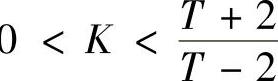，同时还要T>0。

图6-2 三阶系统结构图

【例6-4】 三阶系统结构图如图6-2所示，要求闭环系统特征根全位于s=-1垂线之左，试确定参数K与ζ的稳定域。

解：1）求系统闭环特征式。

clear；syms s K G H D n d phi；G=K/（s∗（0.1∗s+1）∗

（0.25∗s+1））；H=1；

phi=factor（G/（1+G∗H））；[n，d]=numden（phi）；D=d，

程序运行结果D=s^3+14∗s^2+40∗s+40∗K。

2）要求闭环系统特征根全位于s=-1垂线之左，可令s=z-1（即s平面的0是z平面的1，或者s平面的-1是z平面的0），再求解以z为变量的方程。

clear；syms z s K D；D=s^3+14∗s^2+40∗s+40∗K；D=factor（subs（D，[s]，[z-1]）），

程序运行结果D=z^3+11∗z^2+15∗z-27+40∗K。

3）用Lienard-Chipard稳定判据判定系统稳定性。

要系统稳定，首先，特征方程的各项系数均应大于0，有系数a₀=1、a₁=11、a₂=15、a₃=40K-27。所以a₃=40K-27>0，即。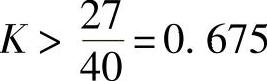

其次，因系统最高阶次n=3，则可计算Hurwitz行列式中偶数阶子行列式（即D₂）应大于0。用程序计算二阶子行列式。

clear；syms a1 a2 a3 a0 K D2；a0=1；a1=11；a2=15；a3=40∗K-27；A=[a1 a3；a0 a2]；D2=det（A），

程序运行结果D2=192-40∗K。

即要系统稳定必须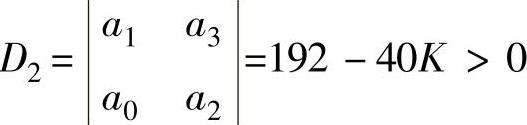，故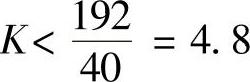。综合两者为0.675<K<4.8。