Simulink动态结构图模型程序下的时域响应仿真优化方案

根据系统的Simulink动态结构图模型，可用linmod（）或linmod2（）函数命令对结构图模型提取一个平衡工作点处的线性模型。有了线性模型，在函数指令方式下的时域仿真不会有任何问题。请注意，在动态结构图模型中，输入与输出环节必须采用“In”与“Out”模块，因为进行何种仿真是由命令确定的。

【例5-33】 已知系统动态结构图仍如图5-29所示。要求系统阶跃响应σ%=20%，t_p=1s。试确定系统参数K与τ，计算系统单位阶跃响应特征量ζ、ω_n、t_p、t_s和振荡次数N，并绘制单位阶跃响应曲线。

解：1）求系统闭环传递函数。

clear；syms s K tau1 omegan G H phi；

G=K/（s∗（s+1））；H=1+tau1∗s；phi=factor（G/（1+G∗H）），

程序运行结果为。

2）求系统参数ζ、ω_n与K。

clear；sigma=0.2；tp=1；[zeta]=sitoze（sigma）；

omegan=pi/（tp∗sqrt（1-zeta^2）），K=omegan^2，b=2∗zeta∗omegan，

程序运行结果为ζ=0.4559、ω_n=3.5299rad/s、K=12.4599、2ζω_n=3.2189，那么

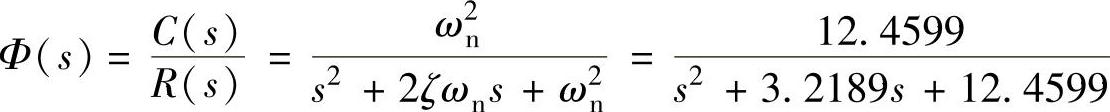
3）求系统参数τ与振荡次数N（5%）。

clear；zeta=0.4559；omegan=3.5299；delta=0.05；[N]=can（1，zeta，delta）；

[tau1]=solve（2∗0.4559∗3.5299=1+12.4599∗tau1）；tau1=vpa（tau1，2），(www.xing528.com)

程序运行结果为τ₁=0.18s、振荡次数N（1.1417）=1、Δ=0.05。

4）绘制系统闭环传递函数对应的单位负反馈等效动态结构图模型，如图5-30所示。

5）验算系统单位阶跃响应特征量t_p、t_s、σ%，并绘制单位阶跃响应曲线。

clear；[a，b，c，d]=linmod2（sx2L0533）；

sys=ss（a，b，c，d）；t1=0：0.001：4；step（sys，t1），grid；

[y，t]=step（sys）；perf（2，y，t）；

程序运行结果为σ%=19.9436%、t_p=0.9876s、t_s（2%）=1.5143s，并绘制出系统单位阶跃响应曲线如图5-31所示。

图5-30 系统动态模型sx2L0533.mdl

图5-31 系统单位阶跃响应曲线

若将模型sx2L0533.mdl中的“In”与“Out”模块分别用单位阶跃信号“Step”与示波器“Scope”模块代替（参见sx2L0533a.mdl），请读者绘制模型并仿真。