根据自动控制原理[10],二阶系统的闭环传递函数与欠阻尼时单位阶跃响应如下。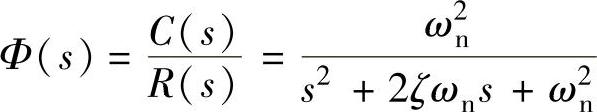 与
与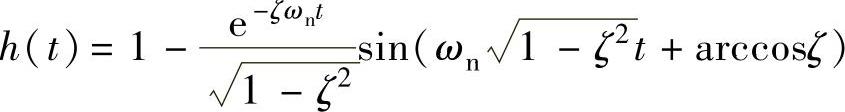 ,阶跃响应上升时间:
,阶跃响应上升时间: ;峰值时间:
;峰值时间: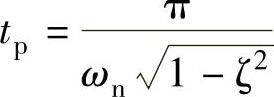 ;阶跃响应超调量:
;阶跃响应超调量: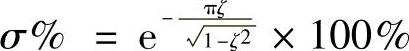 。调节时间:
。调节时间: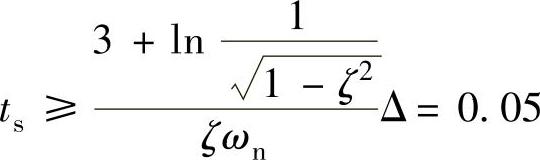
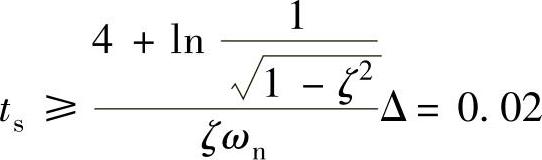
振荡次数:
关于高阶系统时域分析的MATLAB实现,特别是计算其阶跃响应超调量、峰值时间与调节时间等指标,利用作者开发的函数perf(),能够简单方便地计算出结果。利用MATLAB系统函数step()即可绘制其阶跃响应曲线。
【例5-24】 欠阻尼二阶系统的超调量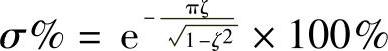 ,试绘制σ%与阻尼比ζ之间的关系曲线
,试绘制σ%与阻尼比ζ之间的关系曲线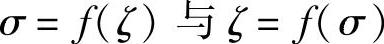 。
。
解:1)用函数命令explot()绘制σ%与阻尼比 之间的关系曲线。
之间的关系曲线。
clear;syms zeta sigma;
sigma=2.7182^(-pi∗zeta/(1-(zeta)^2)^(1/2));
ezplot(sigma,[0,1]),grid;
程序运行后,绘制的曲线 如图5-20a所示。
如图5-20a所示。

图5-20 σ%与ζ之间的关系曲线
2)演算关系式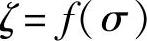 。由
。由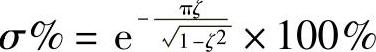 ,得到
,得到 。经恒等变换
。经恒等变换
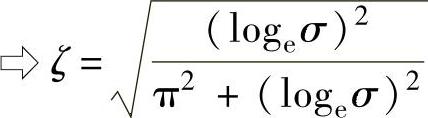 。
。
clear;syms zeta sigma;
zeta=((log(sigma))^2/((pi)^2+(log(sigma))^2))^(1/2);
ezplot(zeta,[0,1]),grid;
程序运行后,绘制的曲线 如图5-20b所示。
如图5-20b所示。
【例5-25】 已知二阶系统传递函数为 ,当ωn=1时,试绘制当阻尼比ζ值从0到1(步长0.1)时二阶系统的单位阶跃响应曲线簇。解:
,当ωn=1时,试绘制当阻尼比ζ值从0到1(步长0.1)时二阶系统的单位阶跃响应曲线簇。解:

运行该程序即得二阶系统单位阶跃响应曲线簇,如图5-21所示。
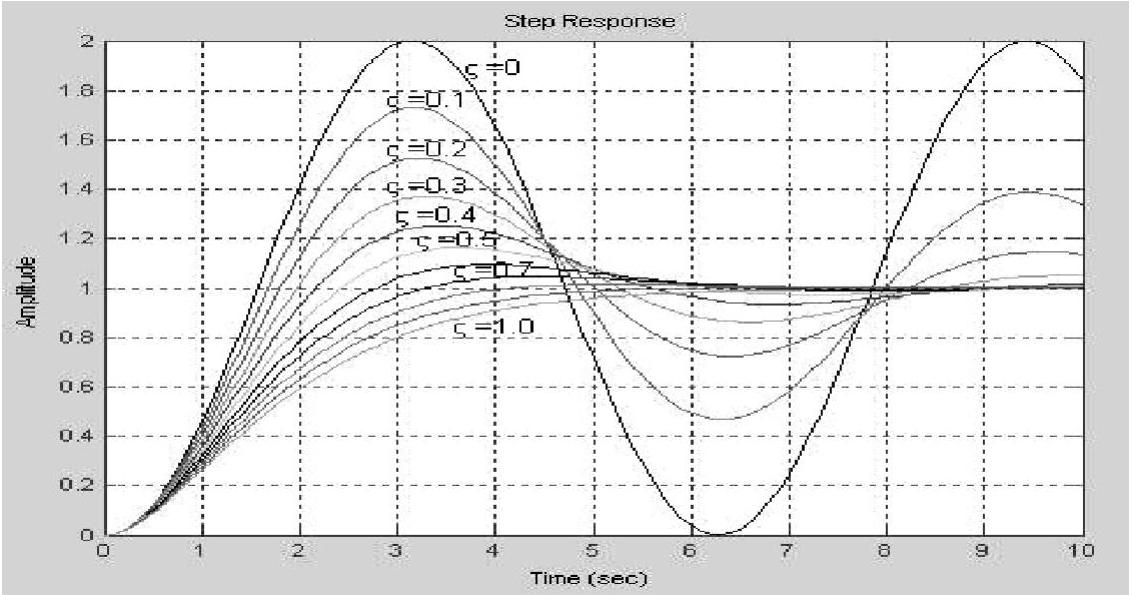
图5-21 二阶系统的单位阶跃响应曲线簇
【例5-26】 已知图5-22所示一阶环节传递函数G(s)=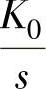 。欲使系统的放大系数为1,调节时间ts=0.1s(5%的误差带),试求K0与Kt的值。
。欲使系统的放大系数为1,调节时间ts=0.1s(5%的误差带),试求K0与Kt的值。
解:1)计算系统传递函数Φ(s)。
clear;syms s K0 Kt G phi;
G=K0/s;phi=simple(G/(1+G∗Kt)),
程序运行后得到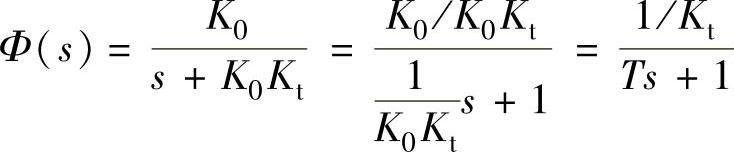 。
。
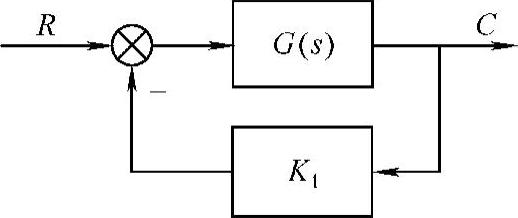
图5-22 一阶环节结构图
2)计算Kt。
clear;syms s K0 Kt G phi;[Kt]=solve( 1/Kt=1
1/Kt=1 ,
, Kt
Kt ),
),
程序运行后得到Kt=1。
3)计算K0。
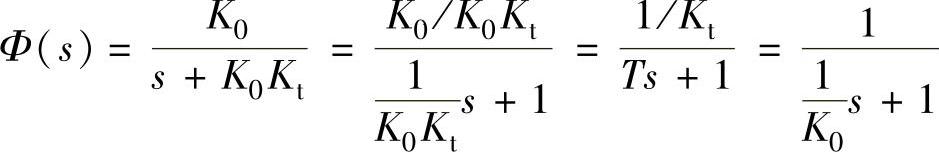
clear;syms K0;[K0]=solve( 3/K0=0.1
3/K0=0.1 ,
, K0
K0 ),
),
程序运行后得到K0=30。
【例5-27】 已知二阶系统闭环传递函数为 。式中,系统阻尼比ζ=0.6;无阻尼振荡角频率ωn=5rad/s。试计算系统单位阶跃响应的特征量tr、tp、σ%、ts与N。
。式中,系统阻尼比ζ=0.6;无阻尼振荡角频率ωn=5rad/s。试计算系统单位阶跃响应的特征量tr、tp、σ%、ts与N。
解:1)由ζ=0.6,ωn=5rad/s,求特征量tr、tp、σ%。

clear;zeta=0.6;omegan=5;[sigma]=zetosi(zeta);[tr,tp]=trtp(zeta,omegan);
程序运行后得到σ%=9.48%、tr=0.5536s、tp=0.7854s。
2)由ζ=0.6,ωn=5rad/s,求特征量ts与N。
clear;zeta=0.6;delta=0.05;omegan=5;[ts]=cats(1,zeta,omegan,delta);
zeta=0.6;delta=0.02;omegan=5;[ts]=cats(2,zeta,omegan,delta);
delta=0.05;zeta=0.6;[N]=can(1,zeta,delta);delta=0.02;zeta=0.6;[N]=can(2,zeta,delta);
程序运行后得到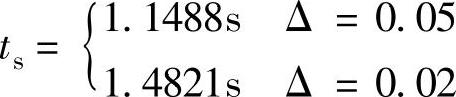
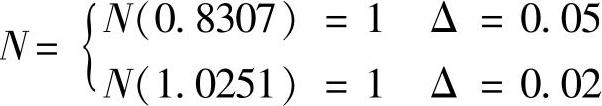
【例5-28】 已知系统结构如图5-23所示。要求系统超调量σ%=16.3%,峰值时间tp=1s,求K与τ。
解:1)求系统闭环传递函数。
clear;syms s K tau phi1 G1 G2 G H1 H2 phi;

图5-23 系统结构图

程序运行后得到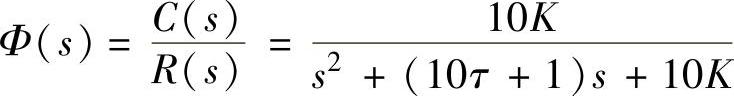 。
。
2)根据二阶系统公式:系统闭环传递函数 ,峰值时间
,峰值时间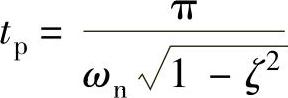 ,超调量
,超调量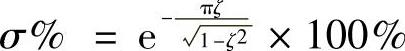 。计算阻尼比
。计算阻尼比 与无阻尼振荡角频率ωn。
与无阻尼振荡角频率ωn。
clear;syms omegan zeta tp;tp=1;sigma=0.163;[zeta]=sitoze(sigma);
omegan=pi/(tp∗sqrt(1-zeta^2));omegan=vpa(omegan,4),
程序运行后得到ζ=0.5与ωn=3.628rad/s。
3)求K与τ。
clear;syms K tau omegan zeta;zeta=0.5;omegan=3.628;[K]=solve( 10∗K=3.628^2
10∗K=3.628^2 );
);
[tau]=solve( 2∗0.5∗3.628=1+10∗tau
2∗0.5∗3.628=1+10∗tau );K=vpa(K,4),tau=vpa(tau,4),
);K=vpa(K,4),tau=vpa(tau,4),
程序运行结果为K=1.316与τ=0.2628。
【例5-29】 一系统结构如图5-24所示。试设计反馈通道传递函数H(s),使整个系统阻尼比ζ提高到ζ1值,但保持系统增益K与无阻尼振荡角频率ωn不变。
解:1)由结构图求系统闭环传递函数。

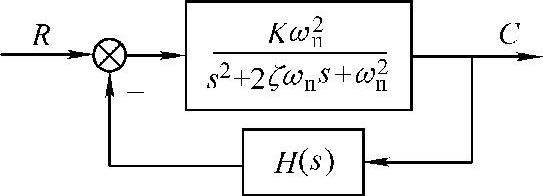
图5-24 系统结构图
观察Φ(s)分母表达式的s一次方系数,为满足题目要求即保持K与ωn不变,应取
H(s)=K1s
2)对比二阶系统标准传递函数 ,求K1与H(s)。因
,求K1与H(s)。因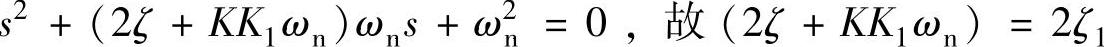 。(https://www.xing528.com)
。(https://www.xing528.com)
clear;syms zeta zeta1 K K1 omegan H s;
[K1]=solve( 2∗zeta+K∗K1∗omegan=2∗zeta1
2∗zeta+K∗K1∗omegan=2∗zeta1 ,K1),H=K1∗s,
,K1),H=K1∗s,
程序运行结果为 、
、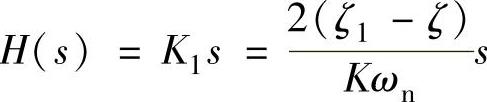 。
。
【例5-30】 已知图5-25所示的单位负反馈系统的开环传递函数 ,当系统的单位阶跃响应曲线如图5-26所示时,试确定K1、K2与a。
,当系统的单位阶跃响应曲线如图5-26所示时,试确定K1、K2与a。

图5-25 二阶系统

图5-26 单位阶跃响应曲线
解:1)演算关系式。

2)求ζ、ωn。
clear;syms sigma zeta omegan tp;
sigma=0.09;[zeta]=sitoze(sigma);
tp=0.8;omegan=pi/(tp∗(1-zeta^2)^(1/2)),
程序运行后得到ζ=0.6083、ωn=4.9478。
3)确定K1、K2与a。
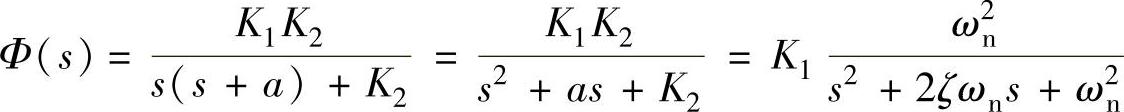
clear;syms k2 a;omegan=4.9478;
zeta=0.6083;K2=omegan^2,a=2∗zeta∗omegan,
程序运行后得到K2=24.4807与a=6.0195,还有K1=2。
【例5-31】 设二阶系统的初始条件为零,其微分方程为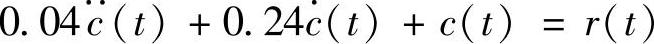 ,
,
试求系统的脉冲响应g(t)、单位阶跃响应h(t)、超调量σ%、峰值时间tp与调整时间ts。
解:1)由微分方程求两端的Laplace变换。
clear;syms t s c r;
l=0.04∗diff(diff(sym( c(t)
c(t) )))+0.24∗diff(sym(
)))+0.24∗diff(sym( c(t)
c(t) ))+sym(
))+sym( c(t)
c(t) );
);
L=laplace(l),R=laplace(sym( r(t)
r(t) )),
)),
程序运行后得到
L=1/25∗s^2∗laplace(c(t),t,s)-1/25∗D(c)(0)-1/25∗s∗c(0)+6/25∗s∗laplace(c(t),t,s)-6/25∗
c(0)+laplace(c(t),t,s)
R=laplace(r(t),t,s)
2)由两端的Laplace变换求系统的传递函数。此时需注意零初始条件,即c(0)=0,
D(c)(0)=0。表达式laplace(c(t),t,s)即C(s)写成C,laplace(r(t),t,s)即R(s)写成R。
clear;syms s R C Z Y;L=1/25∗s∗s∗C+6/25∗s∗C+C;
[C]=solve( 1/25∗s∗s∗C+6/25∗s∗C+C=R
1/25∗s∗s∗C+6/25∗s∗C+C=R ,[C]),
,[C]),
程序运行后得到
3)求ωn,ζ。
对比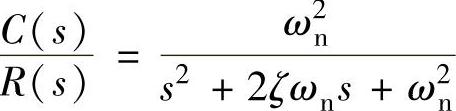 ,可知
,可知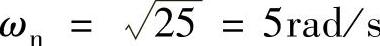
clear;syms omegan zeta;
[zeta]=solve( 2∗zeta∗omegan=6
2∗zeta∗omegan=6 );
);
zeta=subs(zeta,[omegan],[5]),
程序运行后得到ζ=0.6。
4)求脉冲响应 。
。
clear;syms t omegan zeta beta;omegan=5;zeta=0.6;
g=omegan∗exp(-zeta∗omegan∗t)/sqrt(1-zeta^2)∗sin(omegan∗sqrt(1-zeta^2)∗t);
g=vpa(g,3),n=[25];d=[1625];sys=tf(n,d);impulse(sys),grid;
程序运行后得到脉冲响应 ,并绘制系统脉冲响应曲线g(t),如图5-27所示。
,并绘制系统脉冲响应曲线g(t),如图5-27所示。
还可以用绘图函数plot()绘制完全相同的脉冲响应g(t)曲线。clear;t=0:0.001:2;g=6.250∗exp(-3.∗t).∗sin(4.∗t);plot(t,g),grid;
5)求单位阶跃响应 。
。
clear;syms t omegan zeta beta;omegan=5;zeta=0.6;
beta=atan((1-zeta^2)^(1/2)/zeta);
h=1-exp(-zeta∗omegan∗t)/sqrt(1-zeta^2)∗sin(omegan∗sqrt(1-zeta^2)∗t+beta);
h=vpa(h,4),n=[25];d=[1625];sys=tf(n,d);step(sys),grid;
程序运行后得到单位阶跃响应h(t)=1-1.250e-3tsin(4t+0.9273),并绘制系统单位阶跃响应曲线h(t),如图5-28所示。
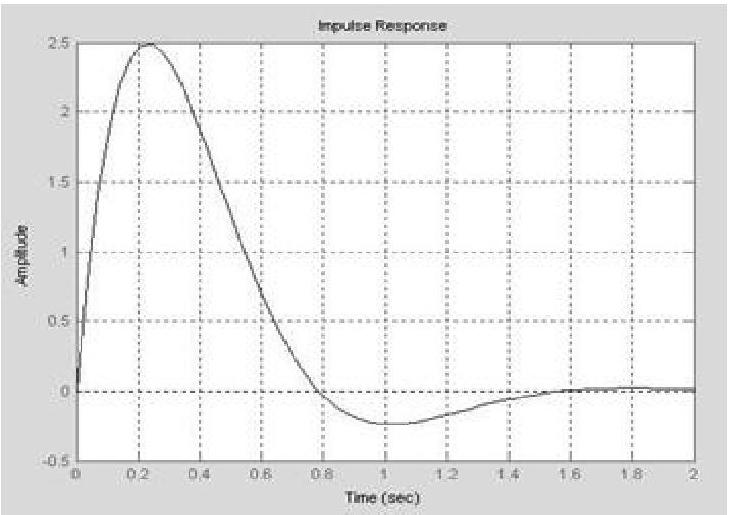
图5-27 系统脉冲响应曲线g(t)
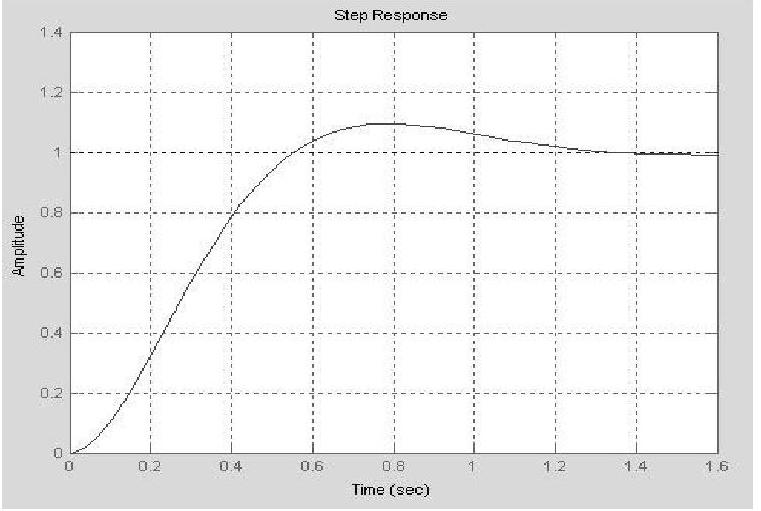
图5-28 系统单位阶跃响应曲线h(t)
还可以用绘图函数plot()绘制完全相同的单位阶跃响应h(t)曲线。
clear;t=0:0.001:1.6;h=1.-1.250∗exp(-3.∗t).∗sin(4.∗t+.9273);plot(t,h),grid;
6)求超调量σ%、峰值时间tp与调整时间ts。
clear;syms omegan zeta omegad sigma tr tp ts ts1 ts2
omegan=5;zeta=0.6;omegad=omegan∗sqrt(1-zeta^2);
beta=atan((1-zeta^2)^(1/2)/zeta),
tr=(pi-beta)/omegad,tp=pi/omegad,
sigma=2.7182^(-pi∗zeta/(1-(zeta)^2)^(1/2)),
delta=0.05;ts=cats(1,zeta,omegan,delta),
delta=0.02;ts=cats(2,zeta,omegan,delta),
程序运行后得到β=0.9273rad、tp=0.7854s、σ%=9.48%、ts=1.1488s(Δ=5%),ts=1.4821s(Δ=2%)。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




