求解微分方程的Laplace反变换方法

用Laplace变换的方法求解微分方程简单而方便。Laplace变换能把微分方程转换为代数方程，而且能把初始条件直接反映在方程中，这便是Laplace变换的奇特功能。

【例5-20】 求解微分方程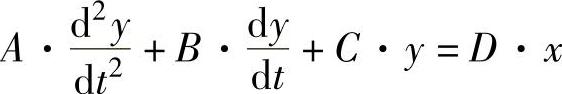。方程中y为输出量；x为输入量。当A=1、B=2、C=-3、D=1且y（0）=0、y·（0）=1、x=e^-t时，绘制微分方程解y（t）的曲线。

解：1）将微分方程进行积分下限为0-的Laplace变换，得到对应的变换方程。

clear；syms t s A B C D y x；

z0=A∗diff（sym（y（t）），2）+B∗diff（sym（y（t）））+C∗sym（y（t））；

z=laplace（z0）；y=laplace（D∗exp（-t）），S=z-y，

程序段运行结果

y=D/（s+1）

S=A∗s^2∗laplace（y（t），t，s）-A∗D（y）（0）-A∗s∗y（0）+B∗s∗laplace（y（t），t，s）-B∗y（0）+C∗la-place（y（t），t，s）-D/（s+1）

2）解变换方程求未知函数的象函数表达式，并进行Laplace反变换求微分方程全解。重写变换方程：改写y（0）为y0，改写laplace（y（t），t，s）为Y，并且计及初始条件y（0）=0、。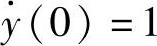

clear；syms t s Y X A B C D；

S=A∗s^2∗Y-A+B∗s∗Y+C∗Y-D/（1+s）；

F=solve（S，Y）；f0=ilaplace（F）；y=simple（factor（f0）），

语句段运行后，得微分方程的全解为

y=

（-2∗exp（-1/2∗t/A∗B）∗sinh（1/2∗t/A∗（B^2-4∗A∗C）^（1/2））∗A∗B-exp（-1/2∗t/A∗B）∗sinh（1/2∗t/A∗（B^2-4∗A∗C）^（1/2））∗B∗D+2∗exp（-1/2∗t/A∗B）∗sinh（1/2∗t/A∗（B^2-4∗A∗C）^（1/2））∗A∗C+2∗exp（-1/2∗t/A∗B）∗sinh（1/2∗t/A∗（B^2-4∗A∗C）^（1/2））∗A∗D+2∗exp（-1/2∗t/A∗B）∗sinh（1/2∗t/A∗（B^2-4∗A∗C）^（1/2））∗A^2+D∗（B^2-4∗A∗C）^（1/2）∗exp（-t）-D∗（B^2-4∗A∗C）^（1/2）∗exp（-1/2∗t/A∗B）∗cosh（1/2∗t/A∗（B^2-4∗A∗C）^（1/2）））/（B^2-4∗A∗C）^（1/2）/（-B+C+A）

3）当A=1、B=2、C=-3、D=1且y（0）=0、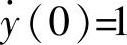时，对微分方程的解绘制曲线。

①求微分方程的全解。参变量代入具体数值的MATLAB程序如下：

clear；syms t s Y X A B C D；

A=1；B=2；C=-3；D=1；

S=A∗s^2∗Y-A+B∗s∗Y+C∗Y-D/（1+s）；

F=solve（S，Y）；y=ilaplace（F），

程序段运行后得到

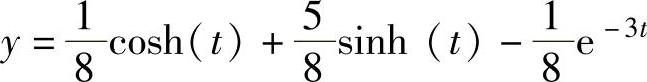
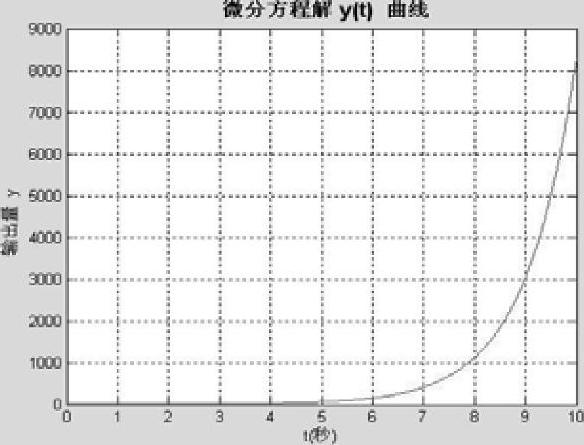
图5-10 微分方程的解y（t）曲线

②对微分方程的解绘制曲线。

clear；t=0：0.01：10；

y=1/8∗cosh（t）+5/8∗sinh（t）-1/8∗exp（-3∗t）；

plot（t，y，-r）；grid；

xlabel（t（秒））；Ylabel（输出量y）；grid on；

title（\fontsize{14}\bf微分方程解y（t）曲线）；

程序运行后即得微分方程解的曲线如图5-10所示。

【例5-21】 电阻R、电感L串联电路如图5-11所示，开关接通前i（0）=0。试求电路与按指数规律衰减的电压u_r（t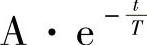）=接通时的电路电流。并绘制A=10V、T=0.5s、R=0.003333Ω、L=0.001H时的变化曲线i（t）。

解：1）根据电工原理，RL网络电流i（t）满足以下微分方程L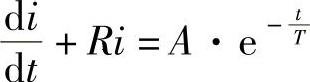，式中。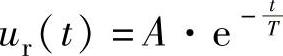

图5-11　RL网络

2）根据用Laplace变换方法解微分方程的步骤计算如下。

①将微分方程进行积分下限为0-的Laplace变换，得到对应的变换方程。

clear；syms t s R L A T T1 i；z00=laplace（L∗diff（sym（i（t）））+R∗sym（i（t）））；

R=L/T1；z0=subs（z00，R，R）；z=factor（z0）；y=laplace（A∗exp（-t/T））；S=z-y，(https://www.xing528.com)

语句段运行结果

S=L∗（s∗laplace（i（t），t，s）∗T1-i（0）∗T1+laplace（i（t），t，s））/T1-A∗T/（s∗T+1）

②解变换方程求未知函数的象函数表达式，并进行Laplace反变换求微分方程的全解。

重写变换方程：改写laplace（ai（t），t，s）为Ai，并且计及i（0）=0。

clear；syms t s L I T T1 A；S=L∗（T1∗s∗I+I）/T1-A/（s+1/T）；

I=solve（S，I）；i0=ilaplace（I）；i=factor（i0），

运行后得到电路电流为。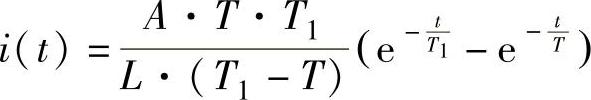

3）当R=0.003333Ω、L=0.001H、A=10V、T=0.5s时，绘制微分方程解的曲线。

clear；t=0：0.001：1；T=0.5；A=10；T1=0.3；L=0.001；

i=-A∗T∗T1∗（-exp（-t/T）+exp（-t/T1））/L/（T-T1）；plot（t，i，-k）；grid；

xlabel（t（秒））；Ylabel（A（安））；grid on；

title（\fontsize{14}\bf电路电流i（t）曲线）；

程序段运行后绘制i（t）曲线如图5-12所示。

【例5-22】 电阻、电感、电容串联电路R、L、C如图5-13所示，试求电路突然接通电源

U_s时电容电压u_c（t）的变化规律，并绘制R=1Ω、L=0.5H、C=1F、U_s=1V、u_c（0）=0V、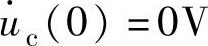时的电容电压u_c（t）变化曲线。

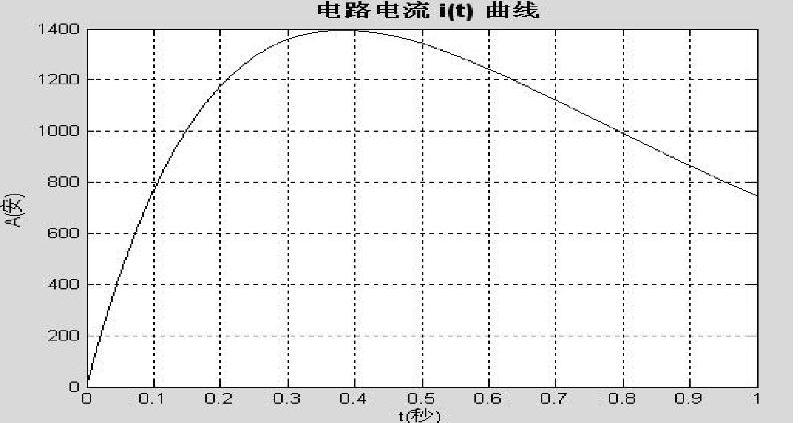
图5-12 电路电流i（t）曲线

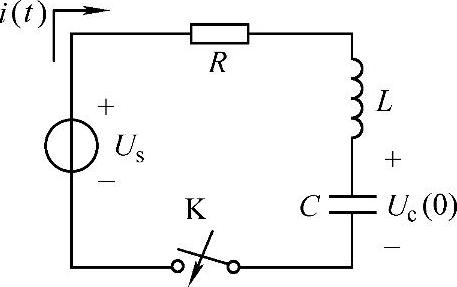
图5-13　RLC网络

解：1）根据电工原理，列写RLC串联电路基尔霍夫电压方程式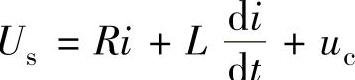，即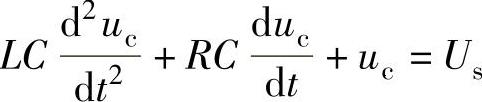

式中，。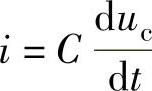

2）将微分方程进行积分下限为0-的Laplace变换，得到对应的变换方程。

clear；syms t s R L C Us uc；

z=laplace（L∗C∗diff（sym（uc（t）），2）+R∗C∗diff（sym（uc（t）））+sym（uc（t）））；

y=laplace（Us∗sym（Heaviside（t）））；S=z-y，

程序段运行结果

S=

-C∗（L∗D（uc）（0）+L∗s∗uc（0）+R∗uc（0））+L∗C∗s^2∗laplace（uc（t），t，s）+R∗C∗s∗laplace（uc（t），t，s）+laplace（uc（t），t，s）-Us/s

3）解算变换方程，必须改写u_c（0）为uc0，改写laplace（uc（t），t，s）为U_c。求反变换，并代入参量值R=1Ω、L=0.5H、C=1F、U_s=1V、u_c（0）=0V、u·_c（0）=0V，对微分方程的解绘制曲线。

clear；syms t s R L C uc0 Duc0 E Uc；

R=1；L=0.5；C=1；Us=1；uc0=0；Duc0=0；

S=-C∗（L∗Duc0+L∗s∗uc0+R∗uc0）+L∗C∗s^2∗Uc+R∗C∗s∗Uc+Uc-Us/s；

F=solve（S，Uc），uc=factor（simple（ilaplace（F））），

ezplot（uc，[07]），grid；

程序段执行后得到

u_c（t）=1-（cos t+sint）e^-t。

程序段执行后还绘制电容电压u_c（t）变化曲线如图5-14所示。

控制系统时域分析的MATLAB实现有两种方法：一是在MATLAB函数指令方式下进行时域仿真；另一种是利用Simulink动态结构图进行时域仿真。以下将逐一介绍。

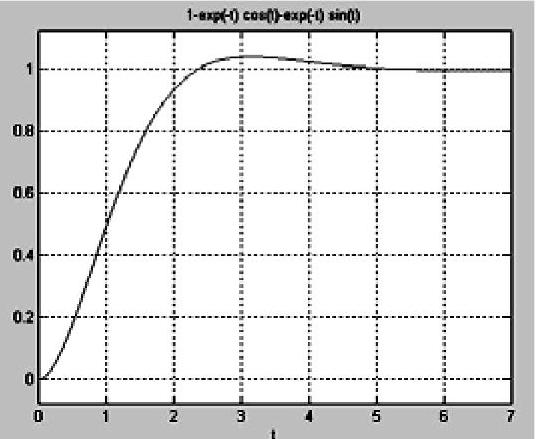
图5-14 电容电压u_c（t）变化曲线