用Laplace变换定义传递函数的方法

传递函数就是在Laplace变换基础上定义的。

【例5-15】 系统的单位阶跃响应为c（t）=1+0.2e^-60t-1.2e^-10t，试求其传递函数。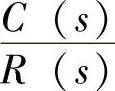

解：1）因系统单位阶跃响应为c（t）=1+0.2e^-60t-1.2e^-10t，还有r（t）=1。

2）求解系统的传递函数

clear；syms s t；r=1∗sym（Heaviside（t））；

R=laplace（r）；c=1+0.2∗exp（-60∗t）-1.2∗exp（-10∗t）；

C=laplace（c）；[n，d]=numden（C/R）；

n=expand（n）；d=expand（d）；phi=n/d，

程序运行后得到系统传递函数为。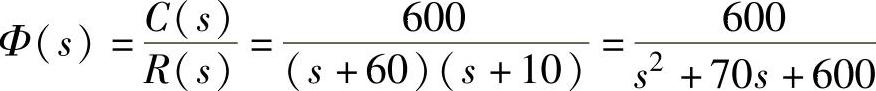

【例5-16】 已知系统非零初始条件下的单位阶跃响应为c（t）=1+e^-t-e^-2t，传递函数分子为常数，试求其传递函数。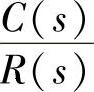

解：1）根据自控原理^[8，9]，非零初始条件下系统响应过程为两个分量叠加而成，一是零初始条件响应分量，二是初始条件响应分量。而且两个分量关于系统响应过程的分析与影响完全相同。那么零初始条件与非零初始条件下系统单位阶跃响应只相差系数。故可设零初始条件下单位阶跃响应为c（t）=1+A₁e^-t-A₂e^-2t，因此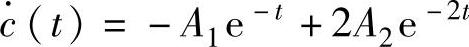。式中，A₁与A₂是待定系数。

2）根据c（t）与的表达式，联立求解当t=0时用A₁与A₂表达c（0）与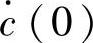的公式。

clear；syms t s A1 A2 c；c=1+A1∗exp（-t）-A2∗exp（-2∗t）；

cp=diff（c）；c=subs（c，[t]，[0]），cp=subs（cp，[t]，[0]），

程序运行后得到c（0）=1+A₁-A₂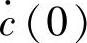，=-A₁+2A₂。

3）根据传递函数定义，必须求系统零初始条件下单位阶跃响应表达式。在系统零初始条件c（0）=0与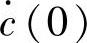=0下可确定A₁、A₂：

clear；syms t s A1 A2 c；[A1，A2]=solve（1+A1-A2=0，-A1+2∗A2=0），

语句运行结果A₁=-2、A₂=-1。

4）系统零初始条件下单位阶跃响应为c（t）=1-2e^-t+e^-2t，据此求其传递函数：

clear；syms s t C c R r phi；

r=1∗sym（Heaviside（t））；R=laplace（r）；

c=1-2∗exp（-t）+exp（-2∗t）；C=laplace（c）；

[n，d]=numden（C/R）；n=expand（n）；d=expand（d）；phi=n/d，

程序运行后得到。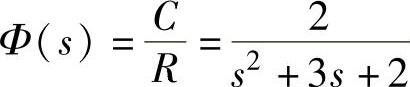

【例5-17】 已知系统输入信号为x（t）=1（t），初始条件为零，系统输出响应如图5-9所示。

试求系统传递函数。

解：1）由解析几何基本原理，图5-9所示的基本图形叠加的函数表达式为y（t）=1·u（t）-u（t-2）。

2）求系统的传递函数的MATLAB语句段如下：

clear；syms s t K；tau=sym（tau，positive）；

x=1∗sym（Heaviside（t））；X=laplace（x）；

y1=1∗sym（Heaviside（t））；y2=-1∗sym（Heaviside（t-2））；

Y=laplace（y1+y2）；Y=factor（Y）；G=Y/X，程序运行后得到系统的传递函数为G（s）=1-e^-2s。

【例5-18】 试求系统传递函数，已知系统零初始条件下微分方程组如下：

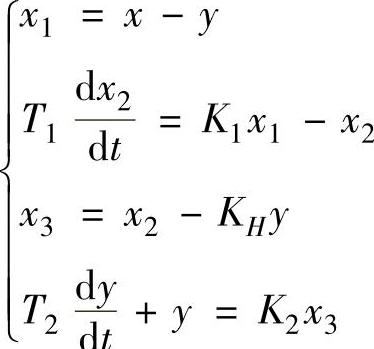(www.xing528.com)

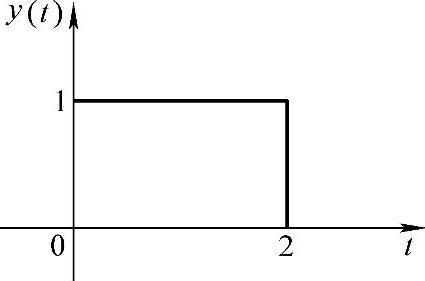
图5-9 输出响应方波

解：1）对微分方程组求其变换方程组。

clear；syms t s T1 T2 K1 K2 KH X1 X2 X3 X Y；

S1Z=laplace（sym（x1（t）））；

S1Y=laplace（sym（x（t））-sym（y（t）））；S1=S1Z-S1Y，

S2Z=laplace（T1∗diff（sym（x2（t））））；

S2Y=laplace（K1∗sym（x1（t））-sym（x2（t）））；S2=S2Z-S2Y，

S3Z=laplace（sym（x3（t）））；

S3Y=laplace（sym（x2（t））-KH∗sym（y（t）））；S3=S3Z-S3Y，

S4Z=laplace（T2∗diff（sym（y（t）））+sym（y（t）））；

S4Y=laplace（K2∗sym（x3（t）））；S4=S4Z-S4Y，

语句段运行结果

S1=laplace（x1（t），t，s）-laplace（x（t），t，s）+laplace（y（t），t，s）

S2=T1∗s∗laplace（x2（t），t，s）-T1∗x2（0）-K1∗laplace（x1（t），t，s）+laplace（x2（t），t，s）

S3=laplace（x3（t），t，s）-laplace（x2（t），t，s）+KH∗laplace（y（t），t，s）

S4=T2∗s∗laplace（y（t），t，s）-T2∗y（0）+laplace（y（t），t，s）-K2∗laplace（x3（t），t，s）

2）解算变换方程组。这里要特别强调，在解代数方程（即象函数方程）列写MATLAB语句时，必须改写所有函数的初始条件f（0）为f0并设置为0，因传递函数定义为零初始条件；改写所有函数f（t）的laplace（f（t），t，s）为F。例如，函数y（t）的laplace（y（t），t，s）为Y。

clear；syms t s T1 T2 K1 K2 KH X1 X2 X3 X Y；x20=0；y0=0；

S1=X1-X+Y；X1=solve（S1，X1）；

S2=T1∗（s∗X2-x20）-K1∗X1+X2；X2=solve（S2，X2）；

S3=X3-X2+KH∗Y；X3=solve（S3，X3）；

S4=T2∗（s∗Y-y0）+Y-K2∗X3；Y=solve（S4，Y）；

G=simple（factor（Y/X）），

G=K2∗K1/（T2∗s^2∗T1+（T2+K2∗KH∗T1+T1）∗s+K2∗K1+K2∗KH+1）程序运行后得到系统的传递函数为

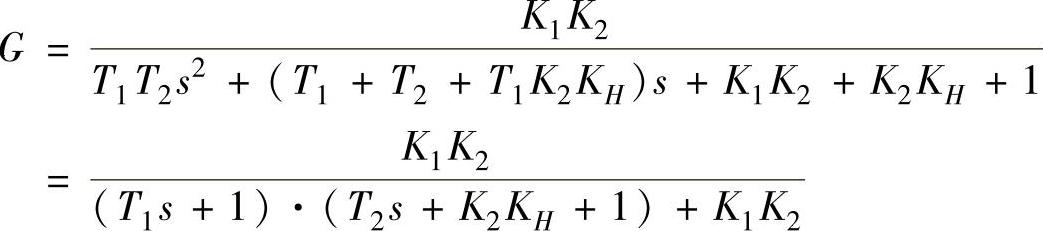
【例5-19】 系统的传递函数为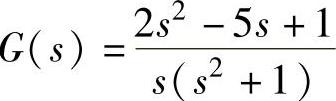，试求系统脉冲响应函数。

解：根据脉冲响应函数的定义g（t）=L^-1[G（s）]。

clear；syms s t；

G=（2∗s^2-5∗s+1）/（s∗（s^2+1））；

g=simple（factor（ilaplace（G））），

程序执行后得到系统的脉冲响应函数为g（t）=L^-1[G（s）]=1+cost-5sint。