Laplace变换的卷积及其定理

根据积分变换理论，已知两个函数f₁（t）与f₂（t），则积分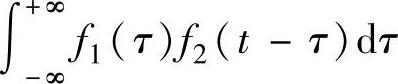叫做函数

f₁（t）与f₂（t）的卷积，记为f₁（t）f₂（t），即。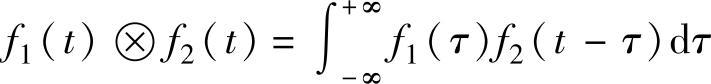

若两个时间函数f₁（t）与f₂（t）都满足条件：当t<0时，f₁（t）=f₂（t）=0，则f₁（t）与f₂（t）的以上卷积式为。请注意两卷积式积分上下区间的变化。

卷积有交换律f₁（t）f₂（t）=f₂（t）f₁（t），其左端f₁（t）f₂（t）叫做f₁（t）卷乘f₂（t），而右端f₂（t）f₁（t）叫做f₂（t）卷乘f₁（t）。与右端式相应的有τ）dτ。若f₁（t）与f₂（t）满足Laplace变换存在的条件，并且有L[f₁（t）]=F₁（s）与L[f₂（t）]=F₂（s），根据积分变换原理，可以证明

L[f₁（t）f₂（t）]=F₁（s）·F₂（s）或L^-1[F₁（s）·F₂（s）]=f₁（t）f₂（t）此两公式叫做Laplace变换的卷积定理。这就是：两个函数卷积的Laplace变换等于该两个函数Laplace变换的乘积或者两个函数Laplace变换乘积的反变换就等于该两个函数的卷积。卷积定理也是Laplace变换的一个重要性质。这个性质不仅被用来求某些函数的逆变换及一些积分值，而且在线性系统的分析中起着重要的作用。

【例5-12】 计算f₁（t）=cost与f₂（t）=sint的卷积。

解：1）用函数卷积定义求解。

clear；syms T s t tau；f1=cos（t）；f2=sin（t）；

bg=subs（f1，t，tau）∗subs（f2，t，（t-tau））；

f1f2=int（bg，tau，0，t），

程序运行后得到。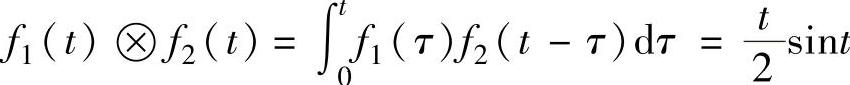

2）用卷积定理验证。

clear；syms T s t tau；f1=cos（t）；f2=sin（t）；

F1=laplace（f1）；F2=laplace（f2）；(www.xing528.com)

f12=ilaplace（F1∗F2），

程序运行后得到相同的结果。

【例5-13】 计算f₁（t）=sinh（kt）与f₂（t）=sinh（t）的卷积。

解：

clear；syms T s k t tau；f1=sinh（k∗t）；f2=sinh（t）；

bg=subs（f1，t，tau）∗subs（f2，t，（t-tau））；

f1f2=int（bg，tau，0，t），

程序运行后得到f₁（t）与f₂（t）的卷积为。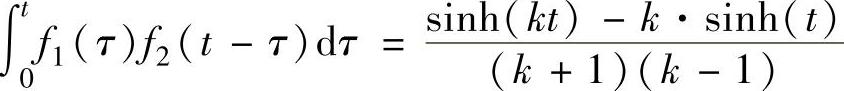

【例5-14】 已知与，F（s）=F₁（s）F₂（s），应用卷积公式求f（t）=L^-1[F（s）]。

解：根据卷积定理有f（t）=L^-1[F（s）]=L^-1[F₁（s）·F₂（s）]。

clear；syms s y；F1=1/s^2；F2=1/（s^2+1）；f=ilaplace（F1∗F2），

程序运行后得到f（t）=L^-1[F（s）]=L^-1[F₁（s）·F₂（s）]=t-sint。