在MATLAB系统中,有专门为求留数而开发的函数命令。先复习抽象的留数概念。
设z0是函数f(z)的孤立奇点,C是z0的足够小的邻域内包含z0点于其内的任何一条正向简单闭曲线,且积分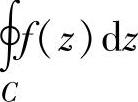 为与C无关的定值,则
为与C无关的定值,则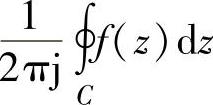 称为f(z)在z0点的留数或残数,记作Res[f(z),z0],即Res[f(z),z0]=
称为f(z)在z0点的留数或残数,记作Res[f(z),z0],即Res[f(z),z0]=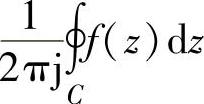 。
。
这是根据复变函数理论定义的留数,非常抽象。在微积分中,计算有理分式函数的积分时,讨论过把分式分解成所谓部分分式的方法。在此,再给出部分分式中留数的直观概念。
若n阶多项式A(s)不含有重根,则以下展开称为部分分式展开,即
式中,p1,p2,…,pn称为极点;R1,R2,…,Rn称为留数;k(s)称为直接项。
若A(s)含有m重根pj,那么相应部分则写为
在高等数学中,留数R1,R2,…,Rn通常用待定系数法来计算。
在MATLAB中求留数的函数命令为residue(),即residue意为留数(部分分式展开)。其调用格式为
[R,p,k]=residue(B,A)
函数命令输入参量为B与A,B与A是分子多项式B(s)与分母多项式A(s)以降幂排列的多项式系数向量,residue()函数是对两个多项式的比值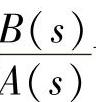 计算,计算结果作为函数的输出量,即函数返回留数向量R、极点向量p,直接项返回到向量k。返回极点向量p的元素是从小到大的顺序排列的,留数向量R中元素与p中元素的位置顺序一一对应。
计算,计算结果作为函数的输出量,即函数返回留数向量R、极点向量p,直接项返回到向量k。返回极点向量p的元素是从小到大的顺序排列的,留数向量R中元素与p中元素的位置顺序一一对应。
需要说明的是,极点的个数n=length(A)-1=length(R)=length(p)。如果length(B)<length(A),则直接项向量为空;否则length(k)=length(B)-length(A)+1。另外,①MATLAB中函数length()的功能为计算向量的维数;②向量k中存放的是假分式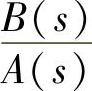 的有理整式的系数,即对应着从右向左依次为s0,s1,s2,s3等项的系数。
的有理整式的系数,即对应着从右向左依次为s0,s1,s2,s3等项的系数。
若A(s)含有m重根pj,即pj=pj+1=…=pj+m-1,函数返回向量仍以极点向量p元素从小到大的顺序排列,而重根部分展开为式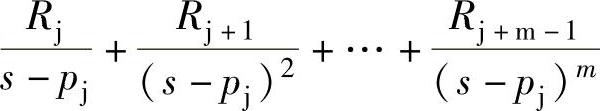 ,即向量R与p元素的顺序与展开式各项从左到右的顺序一致。请看以下示例。
,即向量R与p元素的顺序与展开式各项从左到右的顺序一致。请看以下示例。
【例5-9】 将象函数表达式1)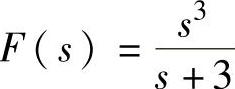 ;2)
;2)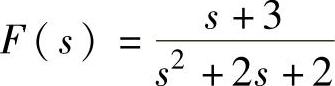 ;3)
;3)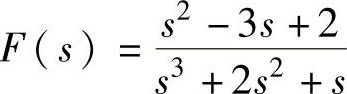 ;
;
4)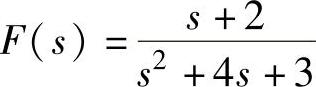 展成部分分式。
展成部分分式。
解:用以下MATLAB语句计算留数、极点与直接项。
1)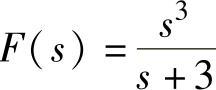 。
。
clear;B=[1000];A=[13];[R p k]=residue(B,A),语句执行后得到(https://www.xing528.com)
R=-27
p=-3
k=1 -3 9
即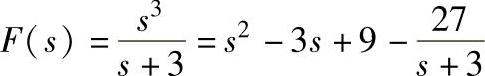 。在此予以验证,其他题目读者自行验证。
。在此予以验证,其他题目读者自行验证。
clear;syms s;
[n,d]=numden(s^2-3∗s+9-27/(s+3)),
语句执行后说明部分分式展开正确。
2)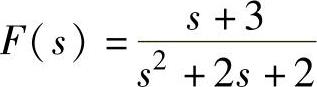 。
。
clear;B=[13];A=[122];[R p k]=residue(B,A),
语句执行后得到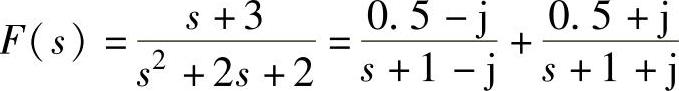 。
。
3)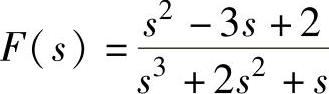 。
。
clear;B=[1-32];A=[1210];[R p k]=residue(B,A),
语句执行后得到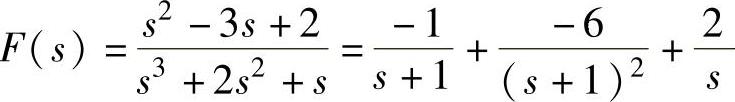 。
。
4)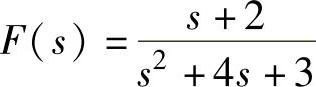 。
。
clear;B=[12];A=[143];[R p k]=residue(B,A),
语句执行后得到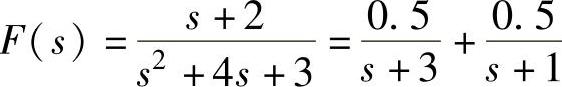 。
。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




