用图形直观展示函数的Laplace变换计算

理论研究中，经常要计算用图形表示的函数的Laplace变换。用图形表示的函数，一般都可以转化为典型基本函数的叠加。那么，这就可以用Laplace变换基本性质来求解。所以必须仔细观察并分析已知图形，运用解析几何知识，将其分解成多个已知基本函数之和，这是解题的基础。还必须熟练典型基本函数的Laplace变换公式。请看示例。

【例5-5】 求图5-1所示单个矩形波的Laplace变换。

解：1）单个矩形波函数图形分析。单个矩形波可看成如图5-2所示两个阶跃函数的叠加。

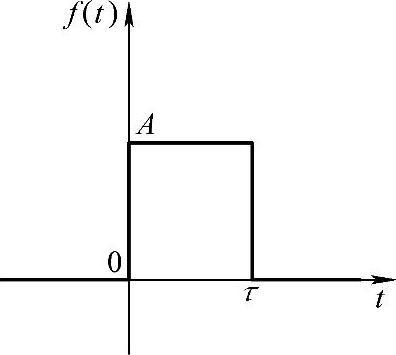
图5-1 单个矩形波

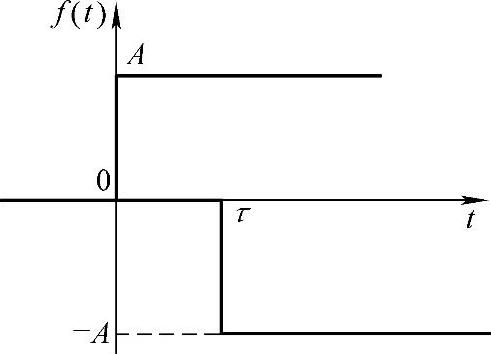
图5-2 等效的两个阶跃函数叠加

图5-2所表示函数的表达式为

f（t）=A·u（t）-A·u（t-τ）

2）求函数Laplace变换的MATLAB语句如下。

clear；syms A t；syms tau positive；

f=A∗sym（Heaviside（t））-A∗sym（Heaviside（t-tau））；

F=laplace（f），

程序执行后得到单个矩形波的Laplace变换为

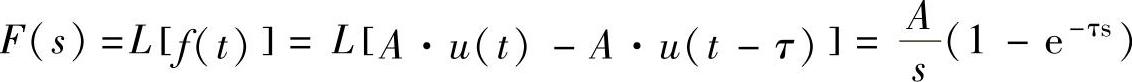
【例5-6】 对图5-3所示的函数，求其Laplace变换。

解：1）图形所示函数分析。图5-3可以看成图5-4所示两个函数的叠加。

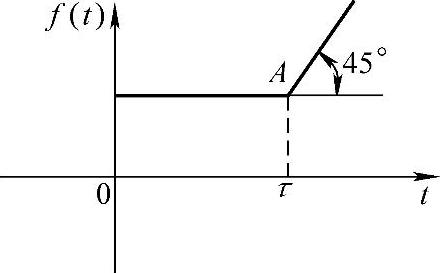
图5-3 抬升的斜坡信号

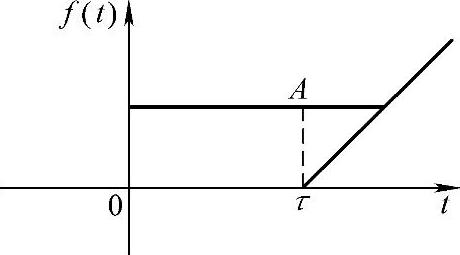
图5-4 阶跃波与斜坡信号叠加

图5-4所表示函数的表达式为

f（t）=A·u（t）+（t-τ）·u（t-τ）

2）求阶跃波与斜坡信号叠加的Laplace变换。

clear；syms A t；tau=sym（tau，positive）；

f=A∗sym（Heaviside（t））+（t-tau）∗sym（Heaviside（t-tau））；

F0=laplace（f）；F=factor（F0），

程序运行后得到图5-4阶跃波与斜坡信号叠加的Laplace变换为

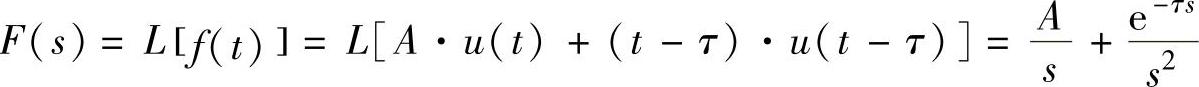
当A=l时，则有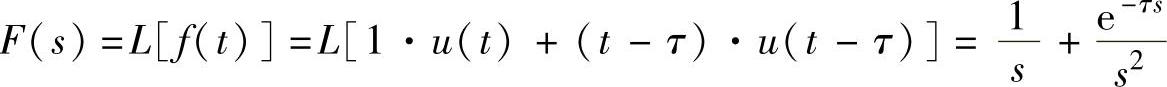

【例5-7】 求图5-5所示单个直角三角形波的Laplace变换。

解：1）图形所示函数分析。图5-5所示的直角三角形波可以看成图5-6所示的3个函数（2个斜坡函数与一阶跃函数）的叠加，即图5-6所表示的函数表达式为

f（t）=t·u（t）-（t-τ）·u（t-τ）-τ·u（t-τ）

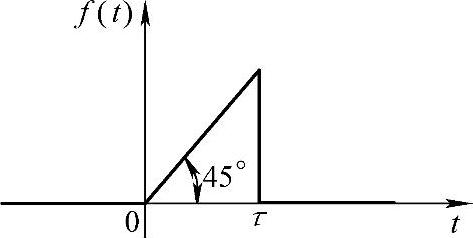
图5-5 单个直角三角形波

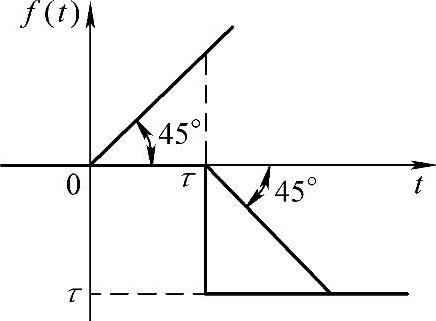
图5-6 三个基本函数叠加

2）求三个基本函数叠加的Laplace变换。

clear；syms A t；tau=sym（tau，positive）；(https://www.xing528.com)

f1=t∗sym（Heaviside（t））；f2=-（t-tau）∗sym（Heaviside（t-tau））；

f3=-tau∗sym（Heaviside（t-tau））；F0=laplace（f1+f2+f3）；F=factor（F0），

程序运行后得到单个直角三角形波的Laplace变换为

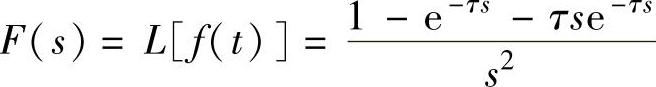
【例5-8】求图5-7所示的正弦周期交流电（振幅A=1）整流半波函数的Laplace变换。

解：本题求解方法很多，在此要用《控制系统MATLAB计算及仿真》中单个正弦半波的拉氏变换结果求解。

1）正弦交流电整流半波函数图形分析。图5-7所示的正弦交流电半波整流函数可以看成图5-8所示的所有第奇数个的单个正弦半波函数的叠加。由《控制系统MATLAB计算及仿真》可知，图5-7所表示的第1个正弦半波函数表达式为。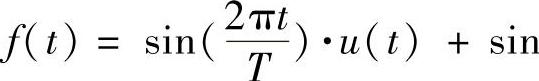

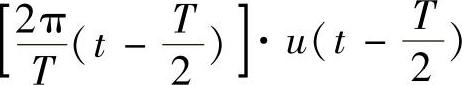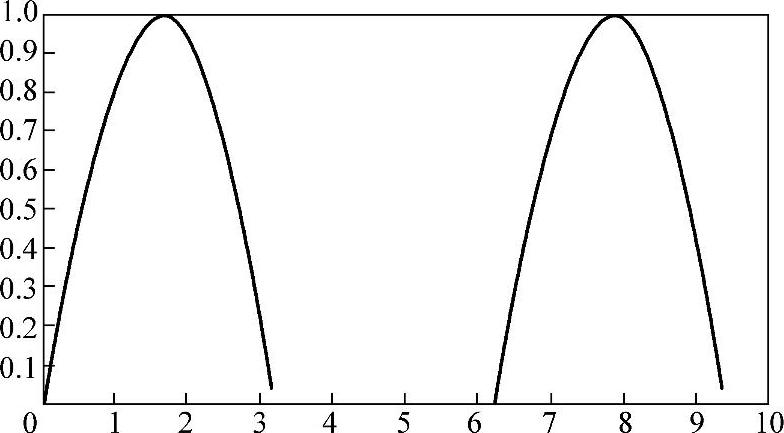
图5-7 正弦交流电半波整流函数

2)第一个正弦半波函数的Laplace变换为

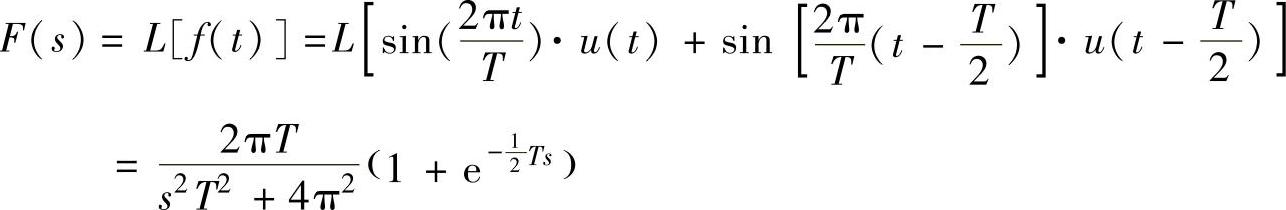
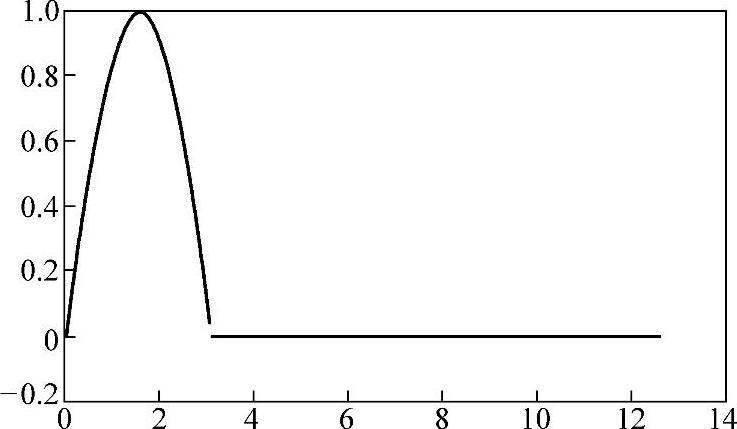
图5-8 等效第奇数个单个正弦半波函数的叠加

3）求第3个半波的Laplace变换。

clear；syms s t；T=sym（T，positive）；

f1=sin（2∗pi∗（t-T）/T）∗sym（Heaviside（t-T））；

f2=sin（2∗pi∗（t-T-T/2）/T）∗sym（Heaviside（t-T-T/2））；

F0=laplace（f1+f2）；F=factor（F0），

语句执行后得到正弦交流电整流全波的第3个半波的Laplace变换为

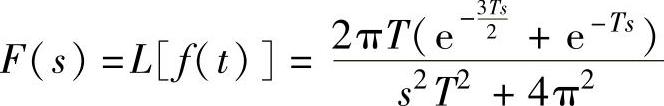
4）求第5个半波的Laplace变换。

clear；syms s t；T=sym（T，positive）；

f1=sin（2∗pi∗（t-2∗T）/T）∗sym（Heaviside（t-2∗T））；

f2=sin（2∗pi∗（t-2∗T-T/2）/T）∗sym（Heaviside（t-2∗T-T/2））；

F0=laplace（f1+f2）；F=factor（F0），

语句执行后得到正弦交流电整流半波的第5个半波的Laplace变换为

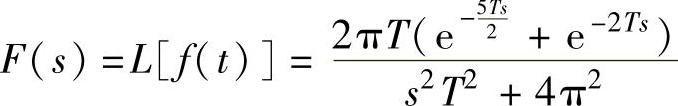
5）由正弦交流电半波整流的第1个、第3个、第5个半波之和，用归纳法推导出整流半波Laplace变换的一般表达式为

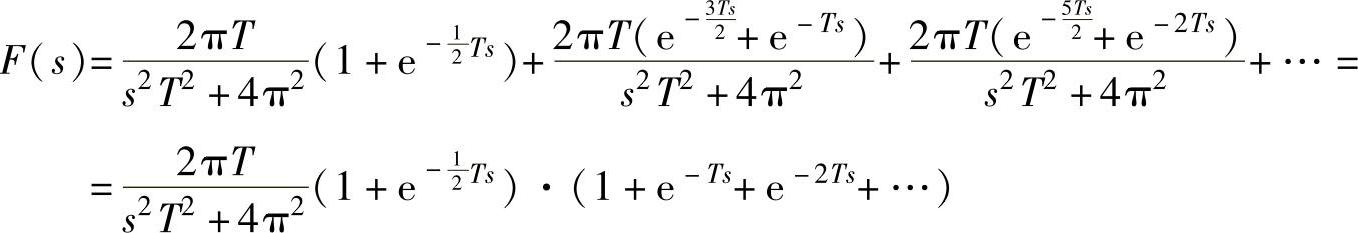
6）求无穷级数（1+e^-Ts+e^-2Ts+…）的和，必须使用MATLAB求和函数symsum（）。

clear；syms s；n=sym（n，positive）；T=sym（T，positive）；

ss=symsum（（exp（-n∗T∗s）），n，0，inf），

语句执行后得到无穷级数（1+e^-Ts+e^-2Ts+…）的和为。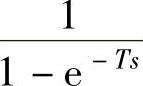

7）整流半波的Laplace变换为

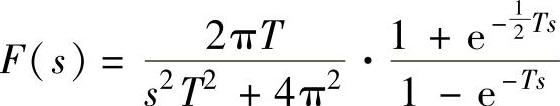
需要说明的是，收敛的幂级数，不论常数项级数还是函数项级数，都有求和的问题。在MATLAB中提供了符号函数求和^[1]的函数命令symsum（），它有以下调用格式。

s=symsum（S，v，a，b）

这种调用格式的功能是，对输入参数S（为求和的对象函数或表达式），在对指定变量v取遍[ab]（即从a到b）中所有整数时，对S求和，即为左端输出参数s。求无穷级数（1+e^-Ts+e^-2Ts+…）的和，正是使用了函数的这种调用格式。