首先计算几个Laplace变换的基本公式。
【例5-1】 求函数f(t)为1)1;2)A·t;3)t2;4)A·eat的Laplace变换F(s)。
解:1)f(t)=1。
clear;syms s t;F=laplace(1,s),
语句运行后得到函数f(t)=1的Laplace变换为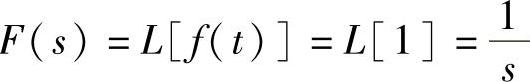 。当读者复习了Laplace反变换后,就会验证变换是否正确。在此仅对此题作验证,其他题读者可自行验证。
。当读者复习了Laplace反变换后,就会验证变换是否正确。在此仅对此题作验证,其他题读者可自行验证。
clear;syms s t;F=1/s;f=ilaplace(F),
语句运行后说明变换正确。
2)斜坡函数f(t)=A·t。
clear;syms A s t;F=laplace(A∗t),
语句执行后得到函数f(t)=A·t的Laplace变换为F 。
。
3)函数f(t)=t2。
clear;syms s t;F=laplace(t^2),
语句执行后得到函数f(t)=t2的Laplace变换为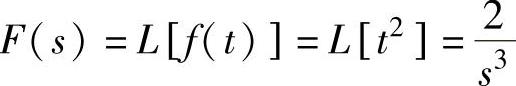 。
。
4)指数函数f(t)=A·eat。
clear;syms A a s t;F=laplace(A∗exp(a∗t)),
语句执行后得到函数f(t)=A·eat的Laplace变换为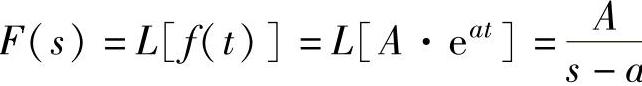 。a
。a
【例5-2】 求函数f(t)为1)cosωt;2)eatsinωt;3)δ(t);4)A·t2+B·t3的Laplace变换F(s)。
解:1)余弦函数f(t)=cosωt。
clear;syms s t omega
laplace(cos(t∗omega)),
语句执行后得到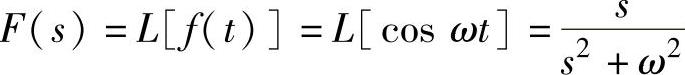 。
。
2)函数f(t)=eatsinωt。
clear;syms s t a omega;
F=laplace(exp(a∗t)∗sin(omega∗t)),
语句执行后得到 。
。
3)单位冲激函数δ(t)。clear;syms s t;f=sym( Dirac(t)
Dirac(t) );F=laplace(f,t,s),
);F=laplace(f,t,s),
语句执行后得到F(s)=L[f(t)]=L[δ(t)]=1。
再次提醒读者注意:①在MATLAB中,单位冲激函数δ(t)规定写成Dirac(t),而且第一个字母D必须为大写;②定义符号变量Dirac(t),在函数sym()的参数引用时两端必须加单引号。单位阶跃函数写成Heaviside(t)的规则同此。
4)函数f(t)=A·t2+B·t3。
clear;syms s t A B;
F=laplace(A∗t^2+B∗t^3),
语句执行后得到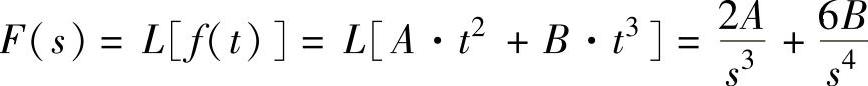 ,由此可得Laplace变换
,由此可得Laplace变换
的线性性质如下。设F1(s)=L[f1(t)]与F2(s)=L[f2(t)],A与B为常数,则有
F(s)=L[A·f1(t)+B·f2(t)]=A·F1(s)+B·F2(s)
这可以执行以下MATLAB语句来验证。
clear;syms s t A B;(https://www.xing528.com)
laplace(A∗(sym( f1(t)
f1(t) ))+B∗(
))+B∗( f2(t)
f2(t) )),
)),
必须说明,在MATLAB系统中,字符串“laplace(f(t),t,s)”即为“F(s)”。
【例5-3】 计算Gamma函数及幂函数tm-1的Laplace变换。
解:1)MATLAB中有很多特殊函数,Gamma函数就是其中之一。积分变换中定义定积分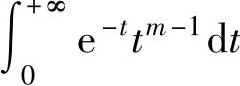 为伽马函数,记为Γ(m),即Γ
为伽马函数,记为Γ(m),即Γ ,m>0。用以下MATLAB语句实现Gamma函数的定义。
,m>0。用以下MATLAB语句实现Gamma函数的定义。
clear;syms s t;m=sym( m
m ,
, positive
positive );
);
f=exp(-t)∗t^(m-1);F=int(f,t,0,inf),
语句运行结果
F=gamma(m)
将tm-1改为tm再运行一次以下语句:
clear;syms s t;m=sym( m
m ,
, positive
positive );
);
f=exp(-t)∗t^m;F=int(f,t,0,inf),
语句运行后得到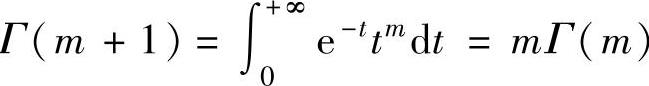 。由上可知,当m为正整数时,有关系式Γ(m+1)=mΓ(m)=m!与关系式Γ(m)=(m-1)!成立。
。由上可知,当m为正整数时,有关系式Γ(m+1)=mΓ(m)=m!与关系式Γ(m)=(m-1)!成立。
必须说明:①当m为正整数时的MATLAB实现语句m=sym( m
m ,
, positive
positive )是必需的,否则不能解算;②阶乘m!=1×2×3×…×m,可用作者自编函数pro.m计算,参见【例1-7】。在MATLAB中有函数命令prod.m计算一个向量或数组所有元素的乘积,这些元素可以不连续,但程序中必须写出全部所有元素,prod()用来求阶乘时也必须写出全部元素。
)是必需的,否则不能解算;②阶乘m!=1×2×3×…×m,可用作者自编函数pro.m计算,参见【例1-7】。在MATLAB中有函数命令prod.m计算一个向量或数组所有元素的乘积,这些元素可以不连续,但程序中必须写出全部所有元素,prod()用来求阶乘时也必须写出全部元素。
2)求幂函数tm-1的Laplace变换F(s)。
求解幂函数tm-1的F(s)可以执行以下MATLAB语句:clear;syms s t;m=sym( m
m ,
, positive
positive );f=t^(m-1);F=laplace(f,t,s),
);f=t^(m-1);F=laplace(f,t,s),
语句执行结果
F=gamma(m)∗s^(-m)
即
tm-1的F(s)为F(s)=L[tm-1]=Γ(m)=(m-1)!
smsm
【例5-4】 求函数1)f(t)=3sint+2cost;2)f(t)=cos(2t+45°);
3)f(t)=e-tu(t)+e-(t-1)u(t-1)+δ(t-2)的象函数F(s)。
解:1)f(t)=3sint+2cost
elear;syms s t;f=3∗sin(t)+2∗cos(t);F=laplace(f,t,s)
程序运行后得到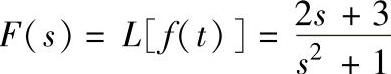 。
。
2)f(t)=cos(2t+45°)
clear;syms s t;f=cos(2∗t+45∗pi/180);F=laplace(f,t,s),
程序运行后得到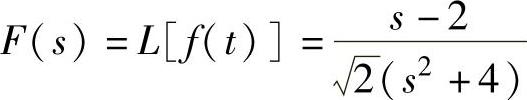 。
。
3)f(t)=e-tu(t)+e-(t-1)u(t-1)+δ(t-2)
clear;syms s t;
fl=exp(-t)∗sym( Heaviside(t-0)
Heaviside(t-0) );
);
f2=exp(-t+1)∗sym( Heaviside(t-1)
Heaviside(t-1) );
);
f3=sym( Dirac(t-2)
Dirac(t-2) );
);
f=f1+f2+f3;F=laplace(f,t,s),
程序运行后得到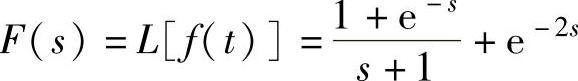 。
。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




