控制系统数学模型优化分析

微分方程是自动控制系统最原始的数学模型，它反映系统动态运行规律。时域分析中要介绍应用拉普拉斯变换定义传递函数，还有基于传递函数图形化形式的动态结构图，即微分方程、传递函数、动态结构图是控制系统的三类基本数学模型。请看以下示例。

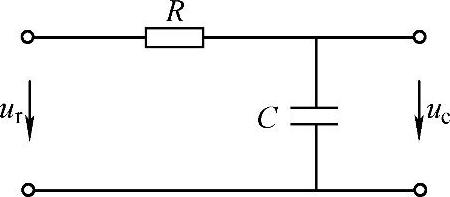
图4-1 阻容RC网络

【例4-1】 阻容RC网络如图4-1所示，试求以u_c作输出，以u_r作输入的微分方程与传递函数模型。

解：1）用符号运算的程序列写微分方程。

clear；syms i ur ucp uc R C；

ur=R∗i+uc；ur=subs（ur，i，C∗ucp），

程序运行后得到微分方程

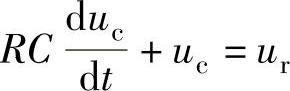
需要说明：①由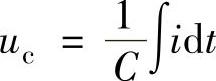有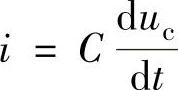；②ucp即为。

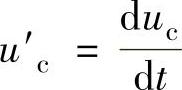2）用RC复阻抗的分压系数求传递函数模型。

clear；syms R C s Ur Uc；

Uc=simple（Ur∗（1/（s∗C））/（R+1/（s∗C）））；G=Uc/Ur，

程序运行后得到传递函数为

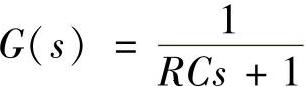
需要说明：①R的复阻抗Z_R=R；②C的复阻抗。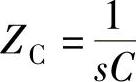

【例4-2】RLC网络如图4-2所示，试求以u_c作输出，以u_r作输入的微分方程与传递函数

模型。

解：1）用符号运算的程序列写微分方程。

clear；syms i ip ur ul ucpp ucp uc R L C；

ip=C∗ucpp；ul=L∗ip；

ur=R∗i+ul+uc；ur=subs（ur，i，C∗ucp），

程序运行后得到微分方程

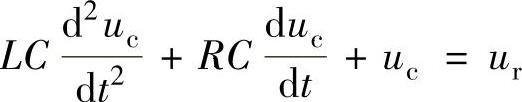
需要说明：①电感两端的电压ul=L∗ip即；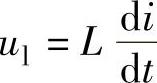

②有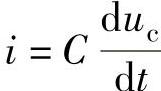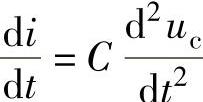，写成ip=C∗ucpp；③ucpp即为。

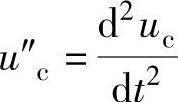2）符号运算求传递函数模型。

clear；syms R C L s Ur Uc；

Uc=simple（Ur∗（1/（s∗C））/（R+s∗L+1/（s∗C）））；G=factor（Uc/Ur），

程序运行后得到传递函数

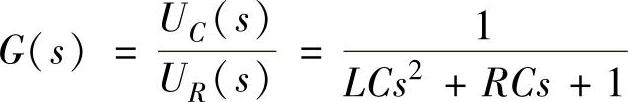
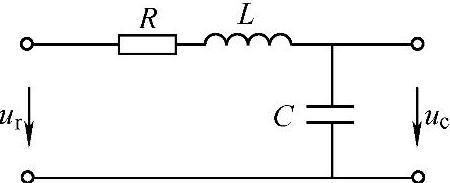
图4-2　RLC网络

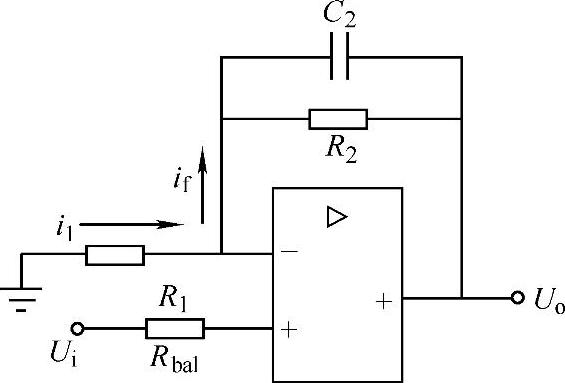
图4-3 同相输入端输入的调节器

【例4-3】 图4-3为控制系统校正时用到的同相输入端输入、反相输入端接地的调节器。试求其传递函数。

解：利用输出与输入复阻抗之比求系统传递函数。

设输入回路的复阻抗为Z₁=R₁。反馈回路的复阻抗Z₂，那么，有

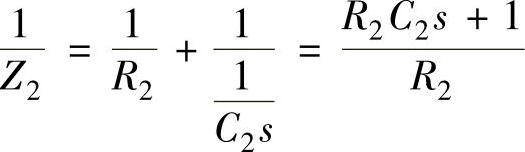
即得

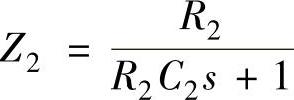
图4-3为运算放大器的同向输入，反向输入端不是“虚地”。根据运算放大器的“虚短”与“虚断”，那么U_-=U₊=U_i，i₁=i_f，即有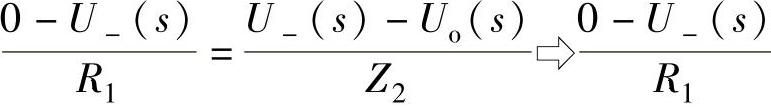

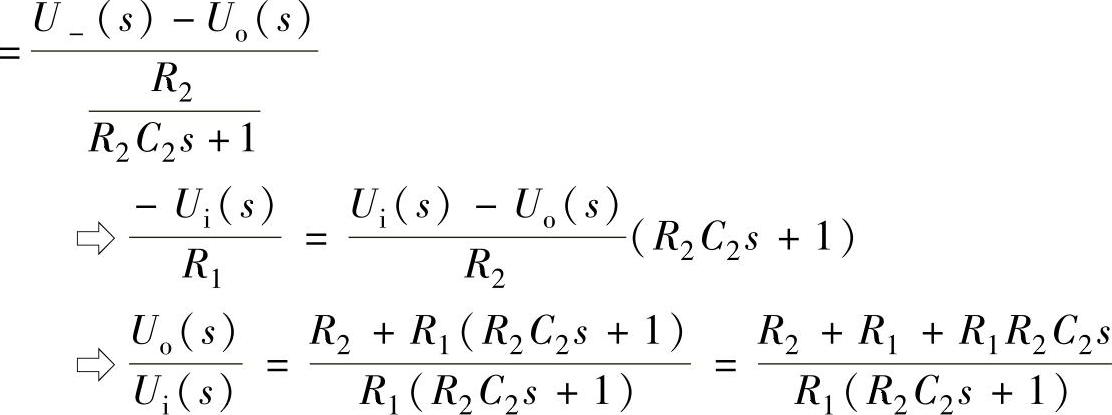
则同相输入端输入、反相输入端接地的调节器传递函数为

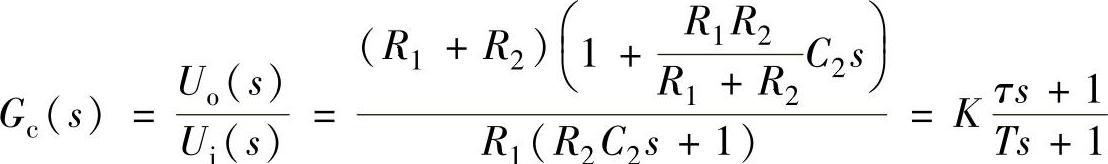
式中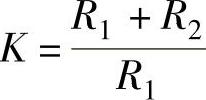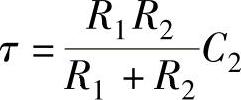，、、T=R₂C₂，而平衡电阻R₀=R₁//（R₂+R₃）。

【例4-4】 试推导负反馈连接的等效传递函数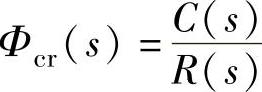与。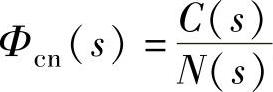

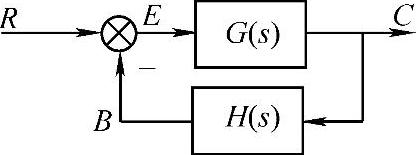
图4-4 负反馈连接(www.xing528.com)

解：1）对负反馈连接（见图4-4）求。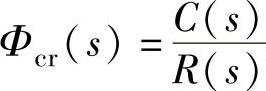

clear；syms R C E B G H；

B=H∗C；E=R-B；C=E∗G；C=expand（C），

程序运行后得到

C=G∗R-G∗H∗C

移项做恒等变换得到

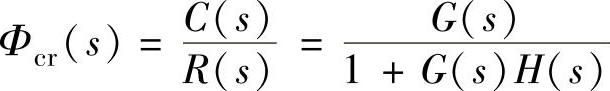
2）对图4-5求。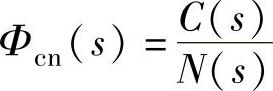

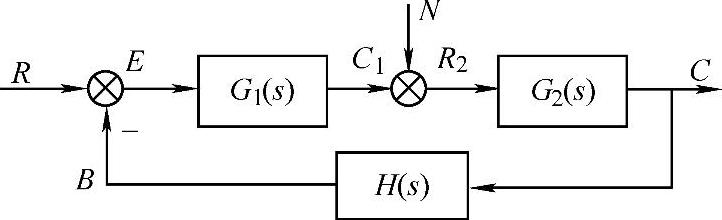
图4-5 带扰动的负反馈连接

clear；syms N C C1 R R2 E B G1 G2 H；

B=H∗C；R=0；E=R-B；C1=E∗G1；R2=C1+N；

C=R2∗G2；C=expand（C），

程序运行结果

C=-G2∗H∗C∗G1+G2∗N

移项做恒等变换得到

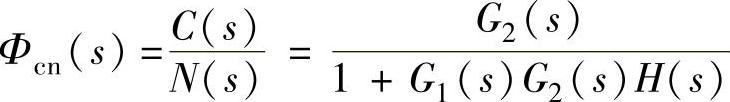
对于较复杂的系统，可能由多个微分方程组成的方程组来描述。要计算其指定输出与输入间的传递函数时，先将系统微分方程组改写成象方程组，其要点是：将微分方程中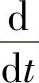换成s，将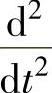换成s²，将∫dt换成，将时域量换成对应的复域量的象方程组，注意两种方程组的结构、项数、系数与阶次完全一致；再对对象方程组求解，指定输出量与输入量间的关系式；最后求传递函数G。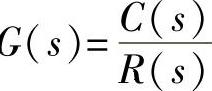

根据系统的象方程组可以绘制系统动态结构（方框）图。其方法如下：

①根据传递函数的定义，按“输入×传递函数方框=输出”绘制每一个传递函数方框。

②以系统的输入作为第一个环节的输入，将第一个环节的输出作为第二个环节的输入，依此类推，以系统的输出作为最后一个环节的输出。按此方法用带箭头的信号线依此连接。

③关注信号综合（叠加）点的信号个数与符号，特别是构成闭环的负反馈信号。

④关注信号引出点的位置以及信号引出的去向。

⑤将图中相同的信号直接用线连接。

⑥在带箭头的信号线旁标注为信号的Laplace变换量。请看以下示例。

【例4-5】 已知系统微分方程为

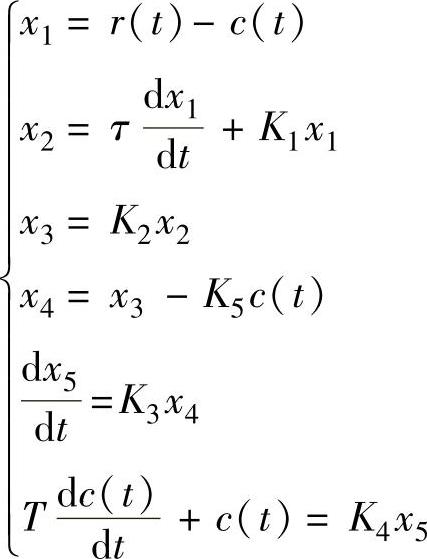
式中，r（t）是输入量；c（t）是输出量；x₁，x₂，x₃，x₄，x₅为中间变量；K₁，K₂，K₃，K₄，K₅，T，τ为常量。试绘制系统动态结构图，并求传递函数。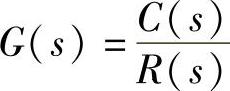

解：1）绘制系统动态结构图如图4-6所示。

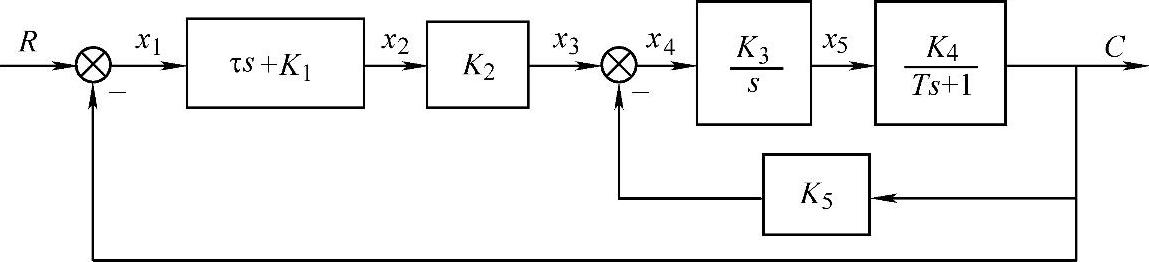
图4-6 双闭环系统

2）用符号运算的程序求传递函数。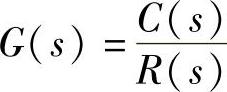

①求R（s）。

clear；syms s C R X1 X2 X3 X4 X5 K1 K2 K3 K4 K5 T tau；

X5=（T∗s+1）∗C/K4；X4=s∗X5/K3；X3=X4+K5∗C；

X2=X3/K2；X1=X2/（tau∗s+K1）；R=C+X1，

程序运行结果

R=C+（s∗（T∗s+1）∗C/K4/K3+K5∗C）/K2/（tau∗s+K1）

②求C（s）。

clear；syms s C R X1 X2 X3 X4 X5 K1 K2 K3 K4 K5 T tau；

[C]=solve（R=C+（s∗（T∗s+1）∗C/K4/K3+K5∗C）/K2/（tau∗s+K1），C），

程序运行结果

C=R/（K4∗K3∗K2∗tau∗s+K4∗K3∗K2∗K1+T∗s^2+s+K5∗K4∗K3）∗K4∗K3∗K2∗（tau∗s+

K1）

即传递函数为

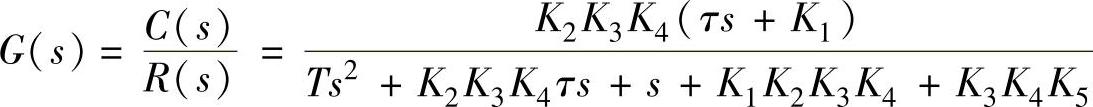
用Simulink建立的系统结构图模型是第4种系统数学模型，在以下系统模型的化简里，显示了其独特的作用。