模糊控制技术的核心思想是模糊集合（Fuzzy Set），由美国加州大学伯克利分校的计算机科学家Lotfi Zadeh于1965年提出。起先，模糊集合的思想受到多数专家的严厉批评，但是，慢慢地又为大多数专家接受了，并最终成为一种全新的人工智能原理。
图16-3给出了经典集合与模糊集合对集合边界的不同解释。对于经典集合A，元素a属于或者不属于A，两者必居其一。与此不同的是，元素a是以介于0和1之间的某个数m隶属于模糊集合
，m称为a在模糊集合
中的隶属度（Member-ship）。
模糊集合反映了人类模糊思维的本质。举例来说，天气温度38℃算是热天，那么温度37℃是否还算是热天？那么36℃呢？那么35℃呢……人们一般还不会否认。当温度到了20℃呢？人们的答案就要动摇了。这里的“热天”就是一个模糊集合。人们对温度的感觉：很热、不是很热、有点热、不热了、很冷等等都可以算是不同的气温对“热天”这个集合
的隶属度m。明显，温度越低，隶属度越小，最后可以认为隶属度为0——在温度极限点与传统集合相同。
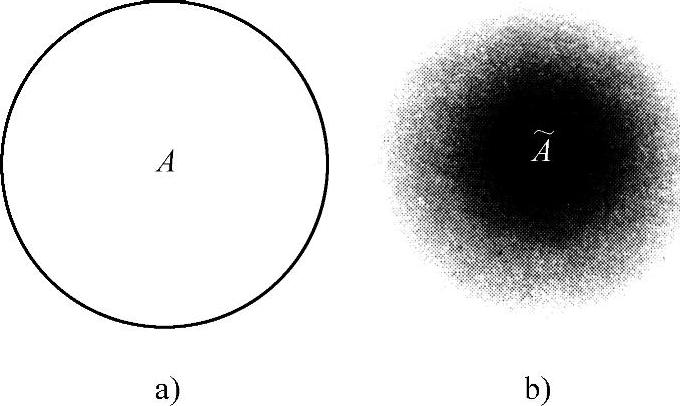
图16-3 经典集合与模糊集和的边界对比
a）经典集合的边界 b）模糊集合的边界
需要计算机进行下述判断还是比较容易的：如果不下雨且气温低于30℃，那么就出门旅游。但是如果希望计算机做如下推断呢——如果天气不错，且温度适中，那么就出门旅游。显然后面的判断难以做出，原因就在于它需要处理的是一个模糊集合。
模糊控制系统的结构如图16-4所示，其核心——模糊控制器包括模糊化单元、模糊推理单元、模糊规则库单元、去模糊化或者称为精确化单元4个部分。模糊化单元将输入精确值（传统集合）转化为模糊集合变量；根据模糊规则可以建立输入、输出模糊变量之间的多条关系；模糊推理决策单元对实际输入的模糊变量与模糊关系进行合成运算，得到模糊输出值；去模糊化单元与模糊化单元正好相反，它将模糊集合变量复原为精确值输出。
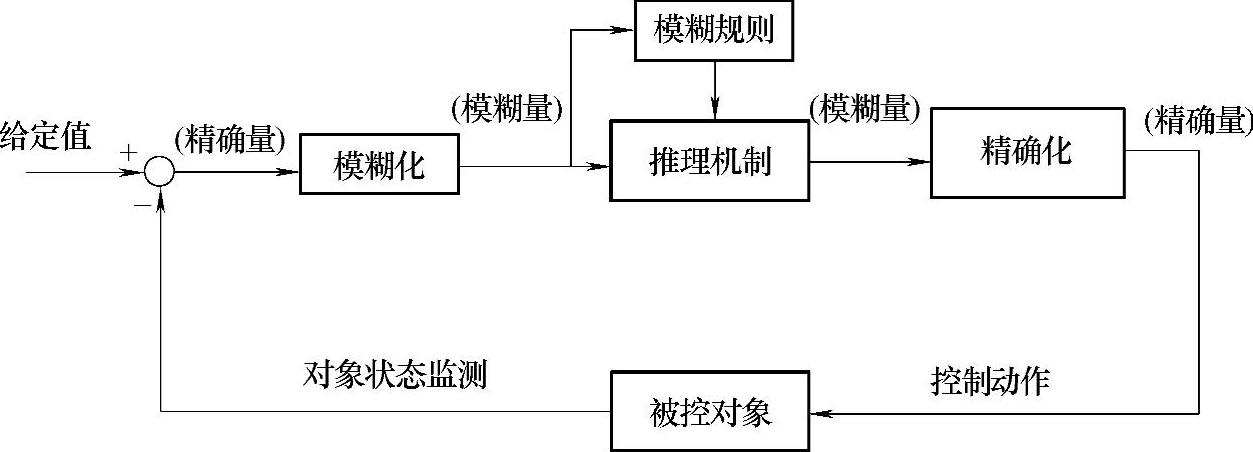
图16-4 模糊控制系统的结构图
一个模糊控制系统的一般设计方法如下：
1）首先，分析待解决问题是否有必要应用模糊逻辑，否则采用常规方法，例如对一个数学模型已知且不存在参数变化或负载干扰的线性反馈系统，使用模糊控制没有太大优势。
2）从现场得到被控设备的所有控制信息。
3）如果被控设备的模型可以得到，开发一个常规控制的仿真程序并研究其性能。
4）确定可以应用模糊控制的功能部分。
5）确定模糊控制的输入与输出变量。
6）定义变量的论域。
7）定义模糊集，并选择相应的隶属度函数形状。对于一个灵敏的变量，选择更多的模糊集合是必要的。
8）制定规则表。上述两步骤的制定非常关键，需要凭借较多的直觉和经验。
9）如果被控设备的数学模型已知，那么可以对采用模糊控制器的系统进行仿真。在此基础上，调整模糊集合和规则表，直到系统性能最优。否则，只能保守地设计模糊控制系统，然后通过设备的运行结果进行调整。
10）实时地实现设计的控制器，并进一步改善其性能。
MATLAB仿真软件中不仅提供了进行模糊运算的相关函数，并且还在SIMULINK软件包中提供了模糊控制工具箱（Fuzzy Control Toolbox），如图16-5所示。该工具箱提供了隶属度函数库（Membership Functions）、模糊控制器（Fuzzy Logic Controller）等建模单元，前者包含了多种常用的隶属度函数，后者则可以方便地以图形界面的方式建立起一个基于模糊逻辑的控制器。
MATLAB用户一方面可以在命令窗口中通过MATLAB命令来构造一个模糊推理系统（Fuzzy Inference System，FIS），另一方面也可以使用图形用户界面（GUI）工具来构造FIS。下面首先使用一个基于模糊控制的小费（tip）计算程序来简要说明模糊控制器的使用过程，然后结合电动机控制介绍其应用。
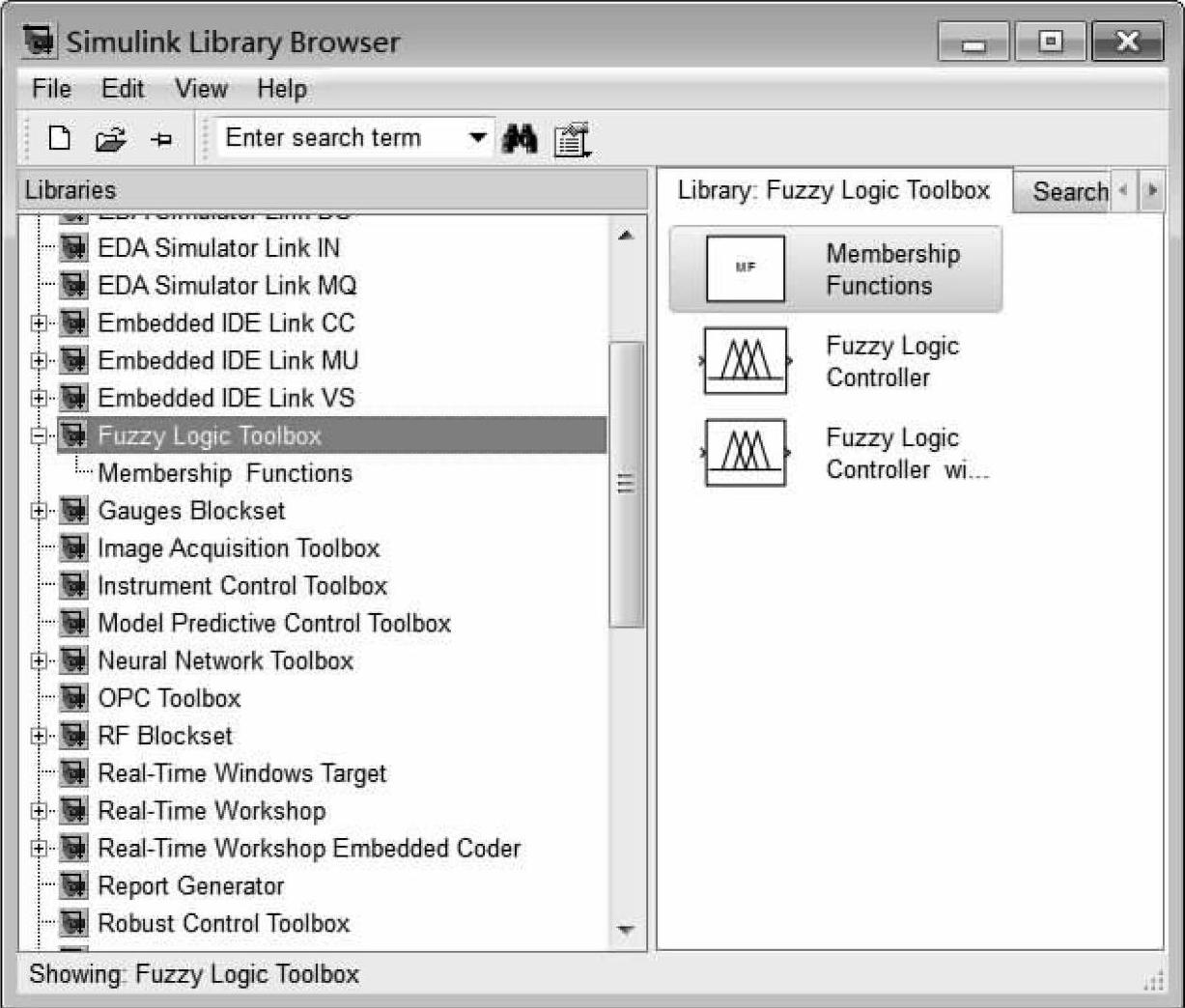
图16-5 SIMULINK中的Fuzzy Control Toolbox界面
图16-5 SIMULINK中的Fuzzy Control Toolbox界面（续）
图16-6给出了MATLAB中用来构造模糊控制器的图形用户界面工具（Fuzzy Logic Tool-box Graphical User Interface Tools）的基本结构。它包括5个GUI工具：FIS编辑器（FIS Edi-tor）、隶属度函数编辑器（Membership Function Editor）、规则编辑器（Rule Editor）、规则浏览器（Rule Viewer）和曲面浏览器（Surface Viewer）。
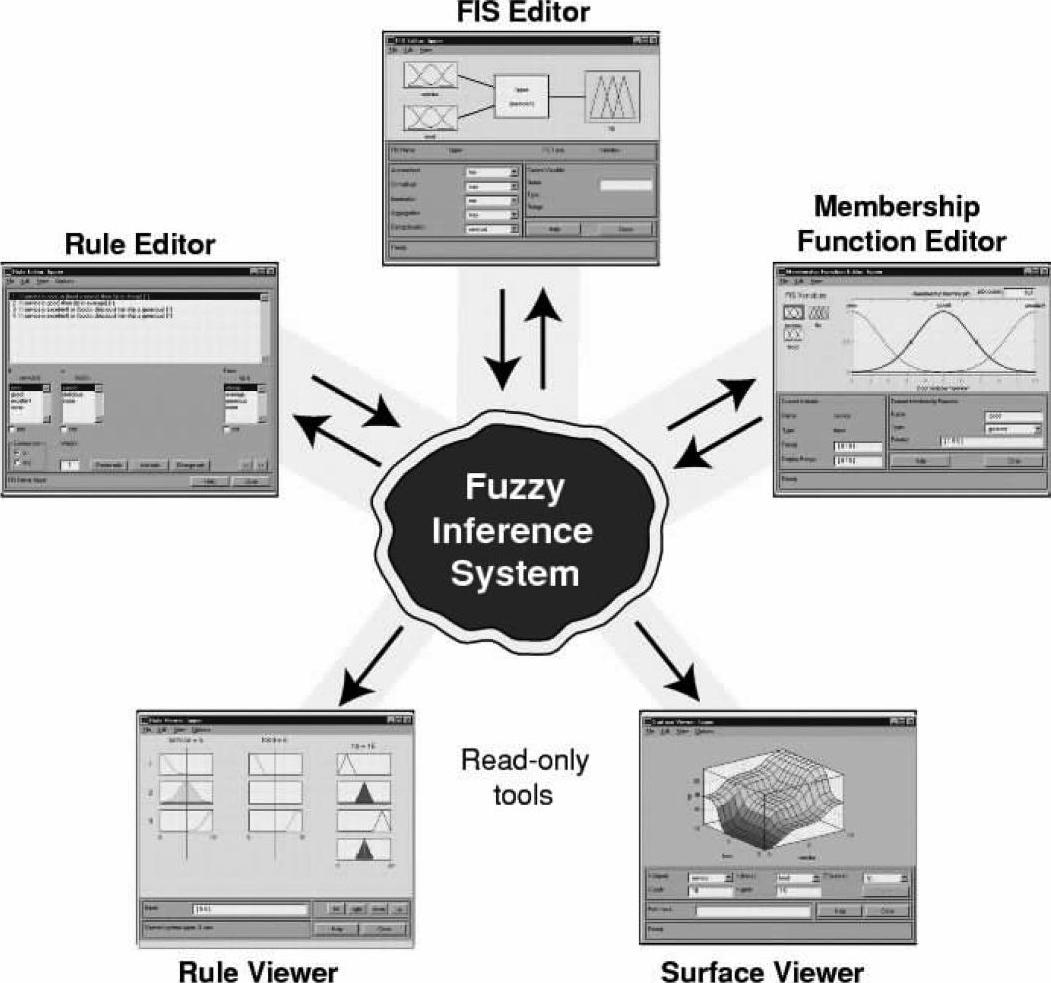
图16-6 MATLAB中模糊控制工具箱的图形用户界面结构
图16-7 FIS编辑器界面
在MATLAB的命令窗口中键入fuzzy后即可出现FIS编辑器界面，如图16-7a所示。也可以直接键入fuzzy tipper，MATLAB系统会自动打开FIS编辑器，并且将系统自带的tipper模糊推理系统在其中显示出来，如图16-7b所示。Tipper是MATLAB自带的一个根据饭店的服务质量（service变量）与食物质量（food变量）进行模糊推理，以决定小费（tip）数量的FIS示例。
FIS编辑器负责处理FIS系统应用层面的问题，例如系统有多少输入与输出变量？变量的名字是什么？可以在file菜单中设置FIS的保存，如图16-8所示将FIS保存到工作空间中。
(www.xing528.com)
图16-8 保存FIS到工作空间或者文件界面
双击图16-7b中的输入变量（service、food）或者输出变量（tip）的图标后，均可出现图16-9所示的隶属度函数编辑器界面。
图16-9 隶属度函数编辑器界面
隶属度函数编辑器用来定义与每个变量相关的隶属度函数的具体形状。本例中使用了3个模糊变量，其中service输入变量对应了3个隶属度函数：poor、good、excellent；food输入变量对应了两个隶属度函数：rancid、delicious；tip输出变量也对应了3个隶属度函数：cheap、average、generous。
双击图16-7b中间的tipper（mandani）图标，可以打开模糊规则编辑器界面，如图16-10所示。规则编辑器用来对描述系统行为的一系列规则进行编辑。本例中根据某消费者的经验制定了三条模糊推理规则。
图16-10 模糊规则编辑器界面
规则浏览器和曲面浏览器用来观察FIS的行为，它们是只读工具，不能用来对FIS进行任何编辑。规则浏览器是基于MATLAB计算环境的图形显示工具，可以用来对FIS系统进行诊断。例如，它可以显示哪些规则处于激活状态，还可以显示隶属度函数形状是如何影响到FIS的输出结果，如图16-11所示。
曲面浏览器用来显示系统的某个输出变量与任意一个或两个输入变量之间的关联性，即是说，它可以对FIS系统绘制输出曲面图，如图16-12所示。
将图16-5a中的模糊控制器拖放到一个新的mdl文件中，建立起图16-13所示的仿真文件。双击图中的Fuzzy Logic Controller后，出现图16-14的对话框。在里面键入前面刚刚保存的tipper模糊推理系统，然后就可以启动图16-13文件的仿真，并且可以看出模糊控制器已经计算出了建议的小费数量为15。
在典型的交流电动机变频调速系统中，模糊控制器通常用作转速控制器、电流控制器、定子电阻的估算、电力电子变换器的PWM算法等单元中。
图16-11 本例中的规则浏览器
图16-12 本例中的曲面浏览器
图16-13 采用模糊控制器的仿真文件
图16-14 模糊控制器的FIS对话框设置
PMSM的直接转矩控制系统中，电动机转矩与定子磁链的闭环控制是通过滞环比较器来实现的，这也可以采用模糊控制器来实现，如图16-15所示。图16-16中分别给出了转矩误差和定子磁链误差的模糊化隶属度函数。其中转矩误差变量定义了NL、NS、ZO、PS、PL等5个隶属度函数，定子磁链误差定义了N、Z、P共3个隶属度函数。表16-1给出了模糊化规则表格，表16-2给出了图16-15中的开关查询表格。
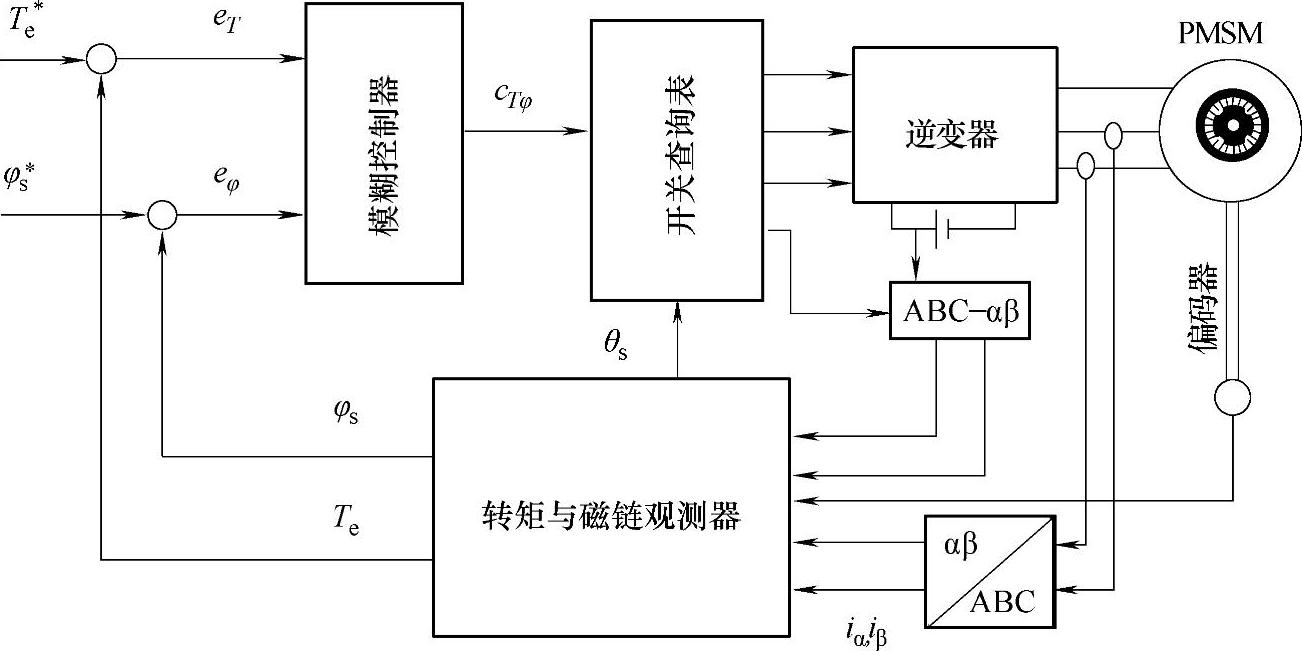
图16-15 采用模糊控制器的PMSM直接转矩控制系统
图16-16 转矩误差、定子磁链误差和输出变量的隶属度函数
表16-1 模糊规则表
表16-2 开关查询表
交流电动机的经典直接转矩控制系统中，电动机的转矩与定子磁链的幅值存在较大的脉动，一方面正是这些脉动量驱动开关查询表输出DTC控制技术特有的PWM波形，另一方面调速系统并不期望有太大的转矩脉动。采用模糊控制器的PMSM直接转矩控制系统的仿真结果如图16-17所示。可以发现采用了模糊控制器的DTC控制系统可以保持快速的动态响应，同时降低了定子电流的谐波分量、转矩脉动与磁链脉动量。
在具体应用中，模糊控制无须建立被控对象的数学模型，对于结构复杂、系统机理认识不清楚、非线性、时变系统都具有较好的控制效果。模糊控制系统设计简单，具有自适应性和鲁棒性，是一种简单、有效的智能控制方法，在工程实践中取得了大量的成功应用。日本日立公司为仙台研制的模糊控制地铁电力机车自动运输系统，使列车在实际运营中节省了10%的燃料，并且停车误差也达到了较高的精度。
图16-17 采用模糊控制器前后的直接转矩控制系统仿真波形对比
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
