深入理解扩展卡尔曼滤波器

卡尔曼滤波器是由美国学者R.E.Kalman在20世纪60年代提出的一种最小方差意义上的最优预测估计的方法，它的突出特点是可以有效地削弱随机干扰和测量噪声的影响。扩展卡尔曼滤波器是卡尔曼滤波在非线性系统中的一种推广形式。

扩展卡尔曼滤波从维纳滤波发展而来，它们都是以均方误差最小为准则的。扩展卡尔曼滤波以状态方程来描述控制对象，而不是维纳滤波的脉冲响应传递函数，使系统描述更加容易，同时它还解决了维纳滤波需要过去所有观测数据和当前观测数据来估计当前数据的缺陷，使其更适合计算机实现，从而使得扩展卡尔曼滤波被广泛运用在工业现场。

设线性离散随机系统为

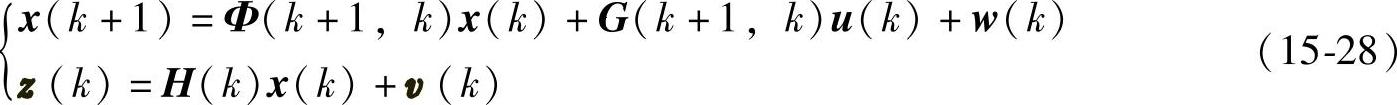
式中，x（k）为n维状态变量；Φ（k+1，k）为状态转移矩阵；G（k+1，k）为输入矩阵；u（k）为r维控制向量（输入）；w（k）为n维随机向量，代表了系统扰动和模型的不确定性；H（k）为观测矩阵；z（k）为m维观测向量；v（k）为m维随机测量噪声向量。

PMSM的状态方程为

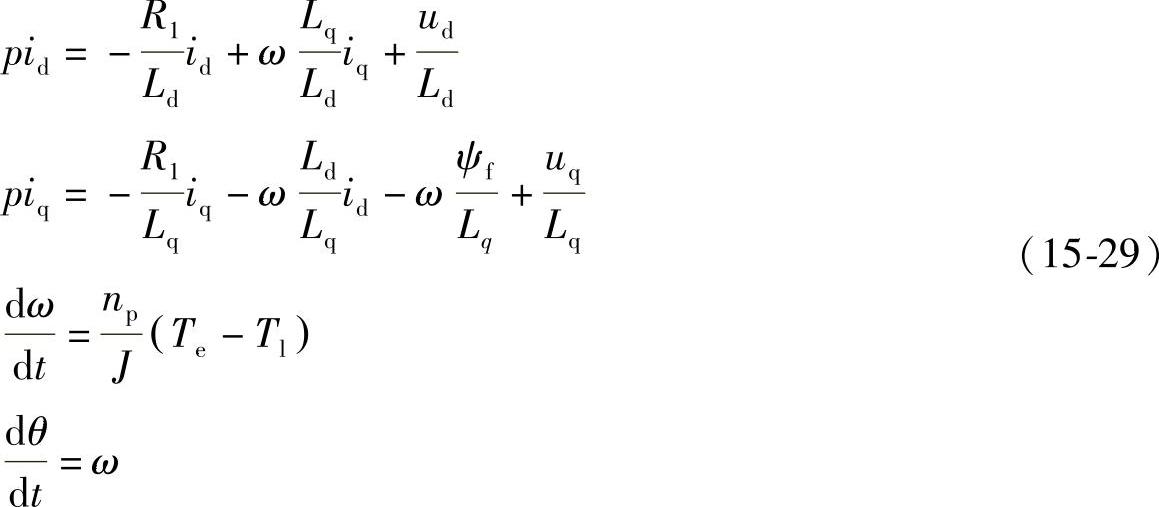
如果J为无限大，则有dω/dt=0。当然，这种假设是不合实际的，但是在EKF中，可将这种不准确性作为系统的状态噪声来处理，在递推计算中由EKF予以必要的校正。并且数字控制系统的采样周期很短，在每个采样周期内的ω可认为是恒定的。

将状态方程和输出方程写成如下矩阵形式：

式中

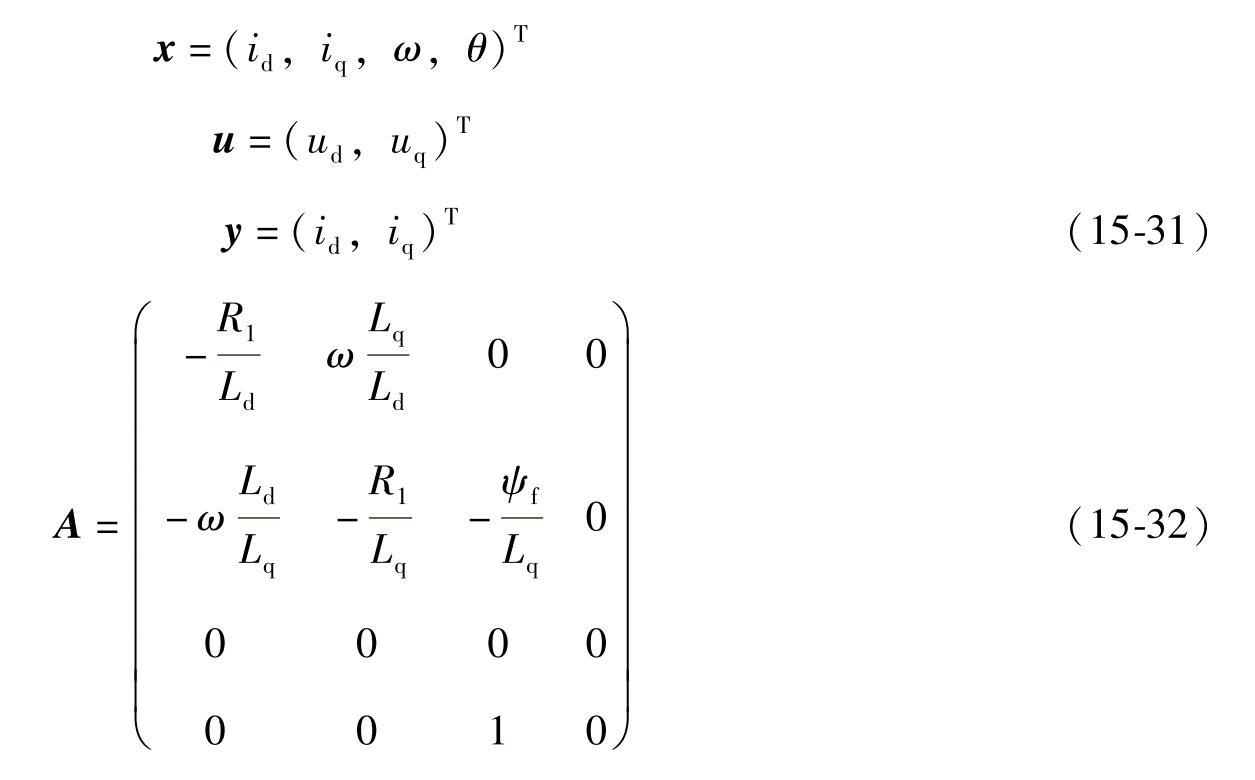
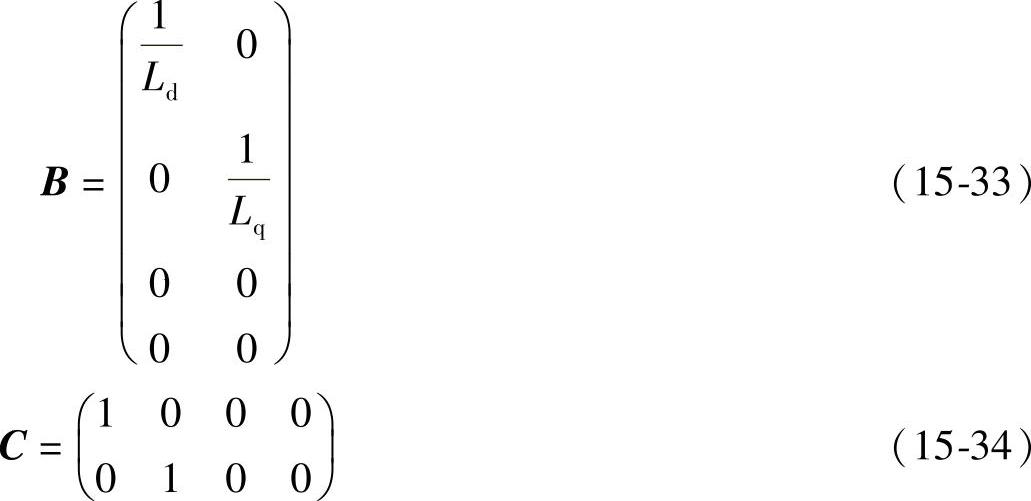
将状态方程式15-30进行离散化处理，可得

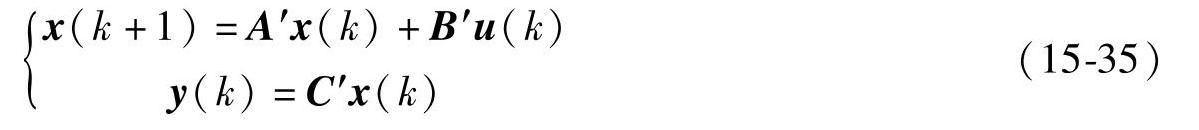
其中

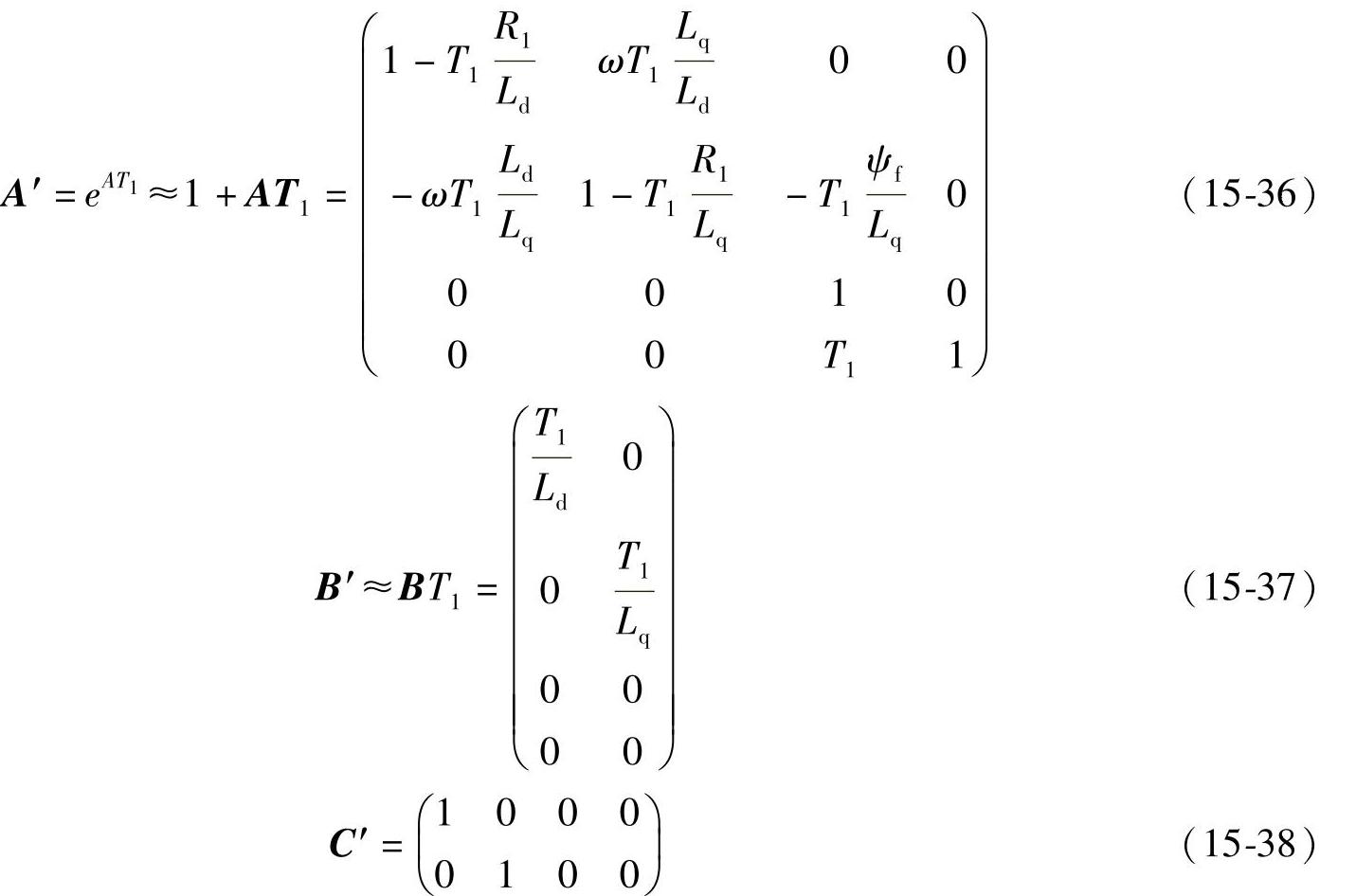
相关雅可比矩阵如下：

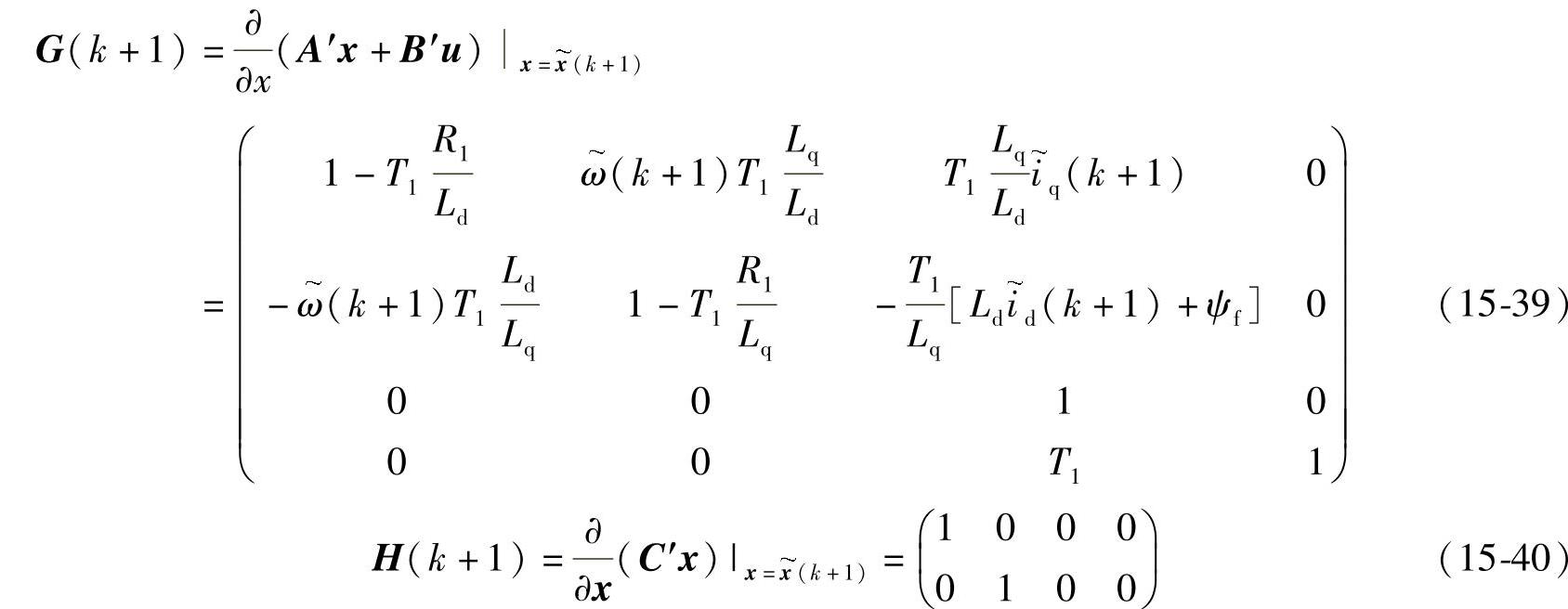
由此，可得PMSM无位置传感器控制的扩展卡尔曼滤波递推中，预测方程为

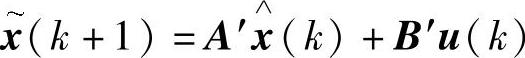
预测误差方差阵为

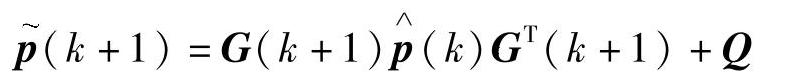
最优增益矩阵方程为(www.xing528.com)

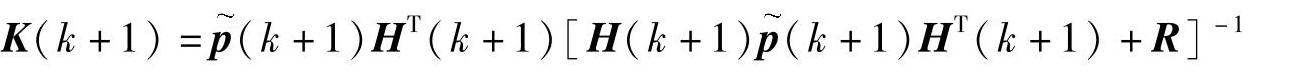
滤波方程为

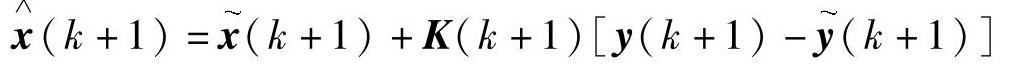
滤波误差方差阵为

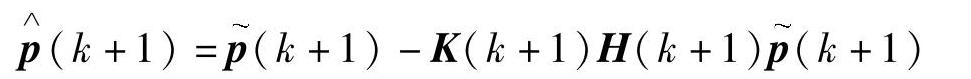
其中，Q称为过程励磁噪声协方差矩阵，R称为观测噪声协方差矩阵。K称为最优增益矩阵。

从上面可以看出，卡尔曼滤波是一种数据处理的递推算法，只要给定初始值x（0）、P（0），根据k时刻测量的u（k）就可以推导计算出k时刻的状态估计x（k），十分适于数字计算机实现。把以上方程用图15-12所示框图表示，可以更清晰地看出卡尔曼滤波过程。图15-12左边部分可称之为滤波回路，对状态变量进行估计和校正，右边部分可称之为增益计算回路，对方差矩阵和增益矩阵进行更新。卡尔曼滤波器预测-校正的计算方式与校正系数的动态修正保证了其性能优于其他滤波算法。

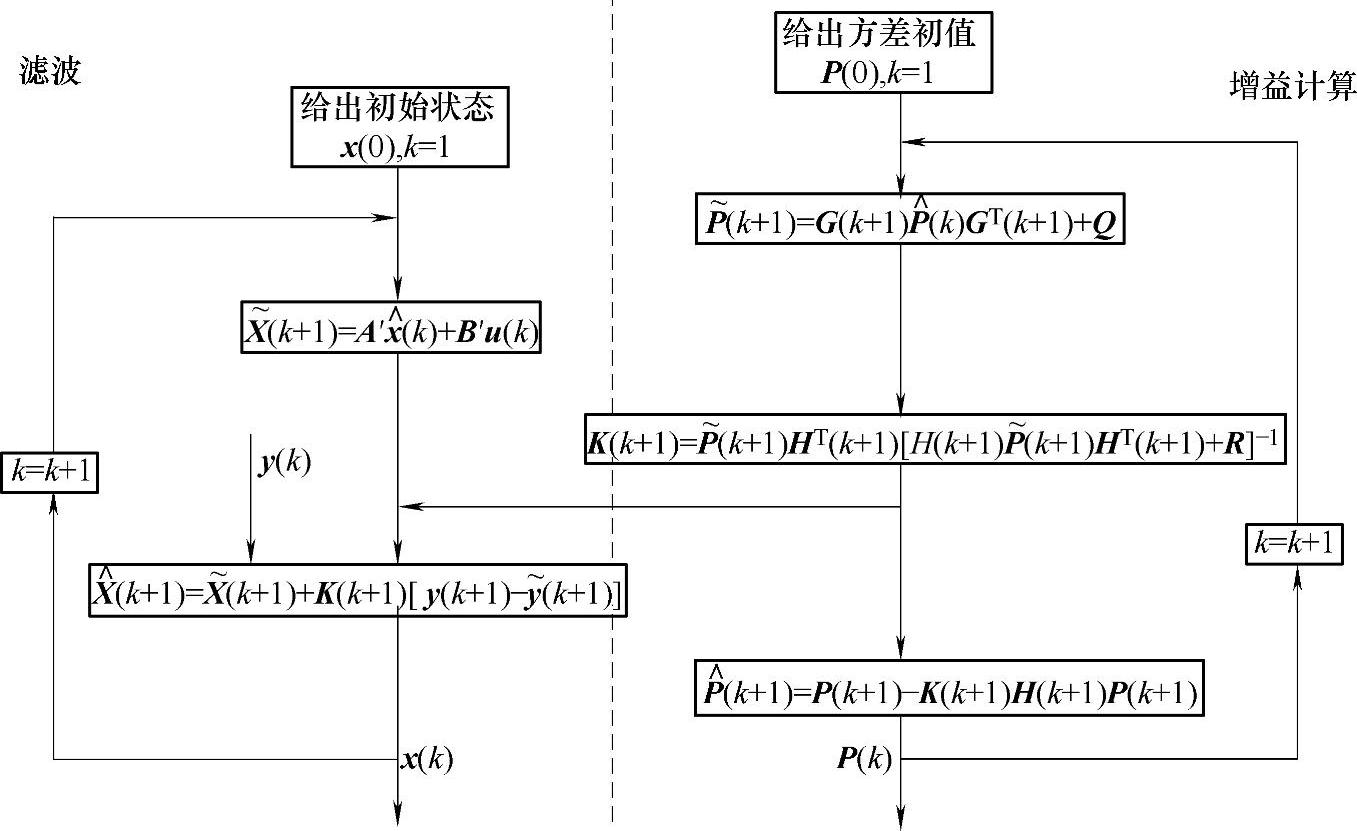
图15-12 卡尔曼滤波器框图

在滤波初值的给定上，欲保证k时刻滤波无偏，只要k=0时刻滤波值无偏即可。当不了解实际系统的初始状态时，可取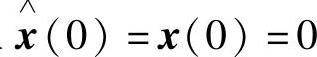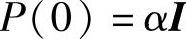，，其中α是一个正数，I为单位矩阵。在此条件下滤波器并不能保证无偏，但只要系统是一致完全随机可控和一致完全随机可观测的，卡尔曼滤波就一定是一致渐进稳定的。随着滤波迭代的进行，选取的初始值x（0）、P（0）对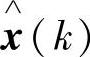，P（k）的影响将逐渐减弱直至消失，估计逐渐趋向无偏。

由上述公式即可实现无位置传感器的扩展卡尔曼滤波算法，基于EKF的永磁同步电动机无位置传感器控制调速系统原理框图如图15-13所示。

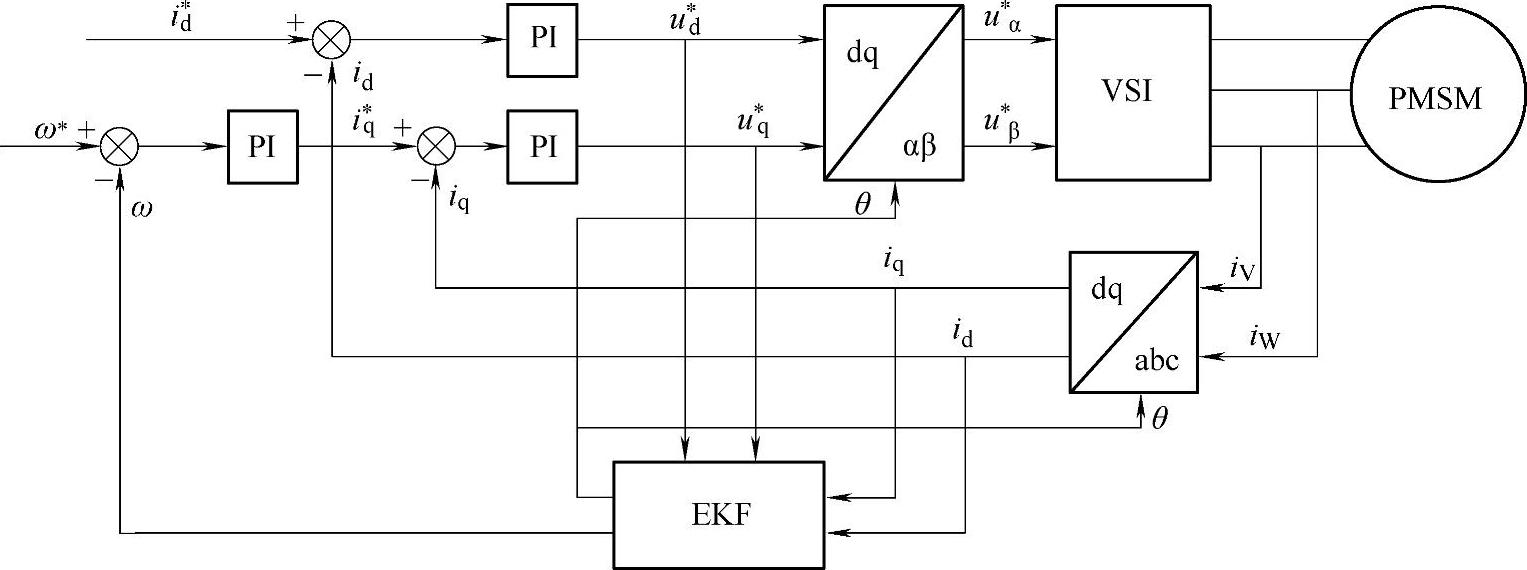
图15-13 基于EKF算法的PMSM无位置传感器控制调速系统原理框图

图15-14为上述内容的MATLAB仿真图，调速系统采用i_d=0的矢量控制。仿真用电动机参数见表15-2，矩阵P以及状态变量x的初始值都取0，Q=diag[0.01，0.01，50，0.01]，R=diag[50，50]，Q、R均保持为常数。

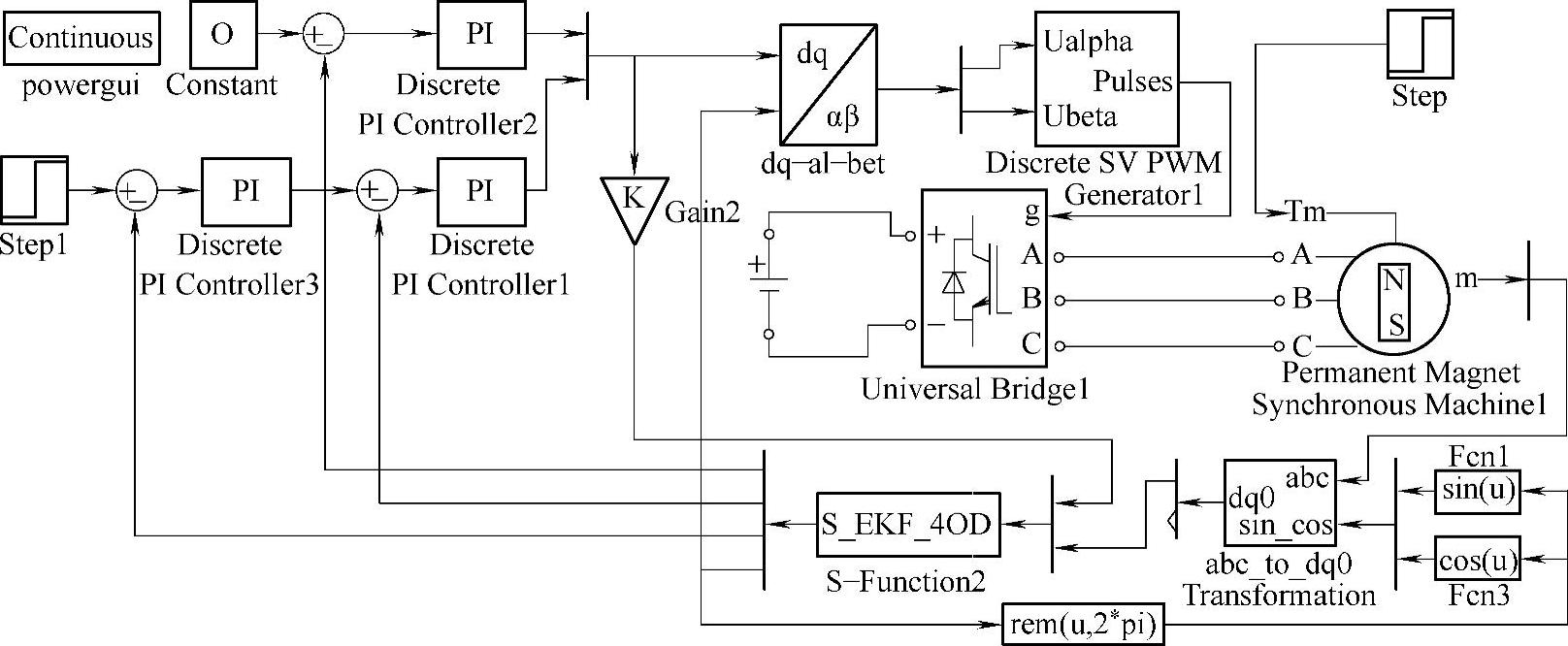
图15-14 基于EKF算法的PMSM无位置传感器控制调速系统仿真框图

表15-2 仿真用电动机参数

仿真中的初始给定速度为314rad/s，在0.4s时加载额定负载7Nm，在0.7s时给定速度增加到628rad/s。图15-15为预测速度与实际速度波形，图15-16为预测转子位置（曲线2）与实际转子位置（曲线1）波形。从这两幅图来看，EKF算法对电动机转子的实际速度与位置的跟踪都具有较高的精度，且具有很强的抗负载扰动能力。

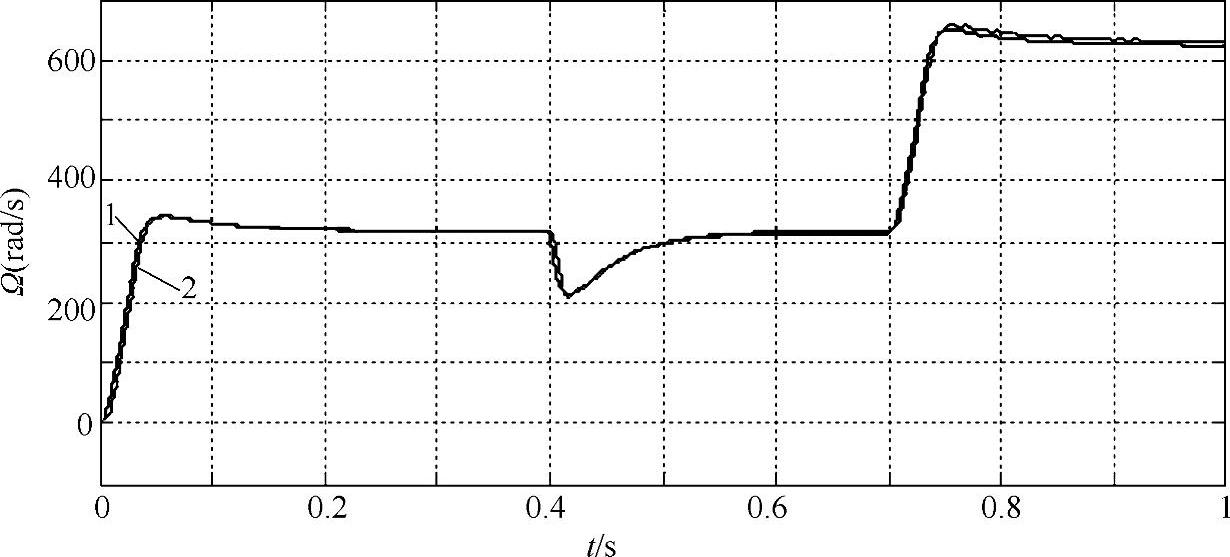
图15-15 仿真中电动机的预测速度与实际速度波形

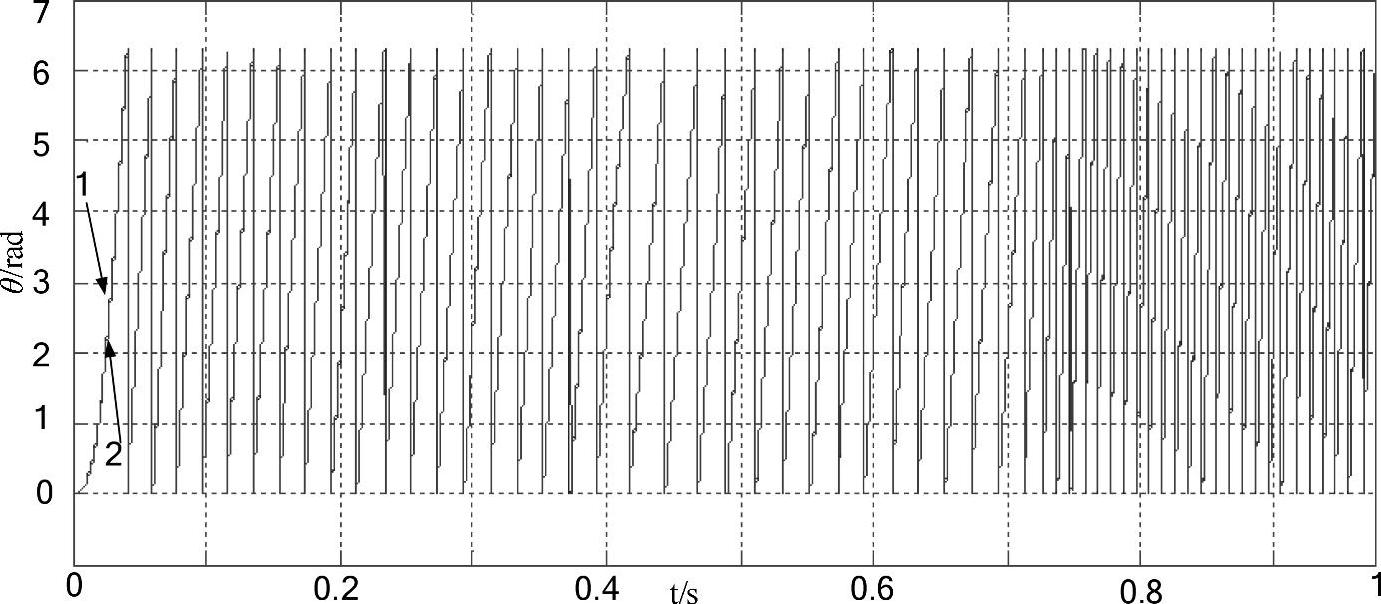
图15-16 仿真中电动机预测位置与实际位置波形