MRAS控制系统中基于电动机模型的速度观测

在S.Tamai将模型参考自适应（MRAS）方法引入到交流电动机调速领域后，MRAS很快在电动机的转速和参数辨识方面得到了广泛应用。

MRAS方法使用两个模型，其一为不含有待观测变量（例如电动机转速）的参考模型，另一个是含有待观测变量的可调模型。两个模型均输出同一个变量，利用两个模型输出变量的差值对可调模型中的待观测变量进行快速调节，通过设计出合适的调节规则，那么就可以在足够短的时间内观测出未知变量。

将dq坐标系下PMSM电动机定子电压改写成如下形式：

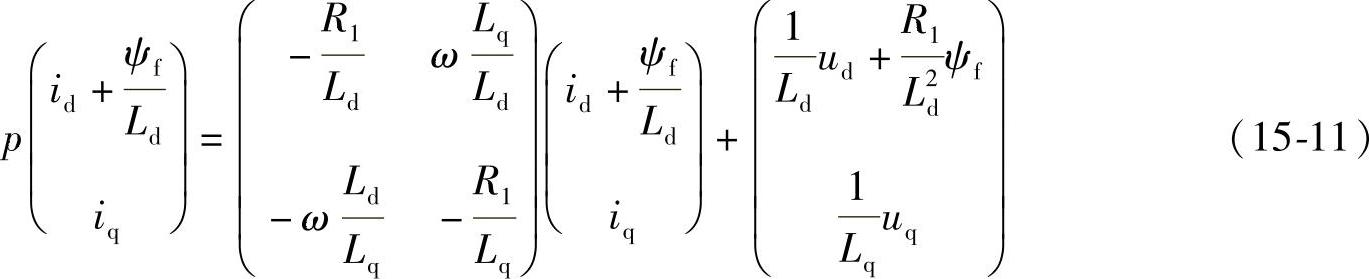
并记一组新变量为

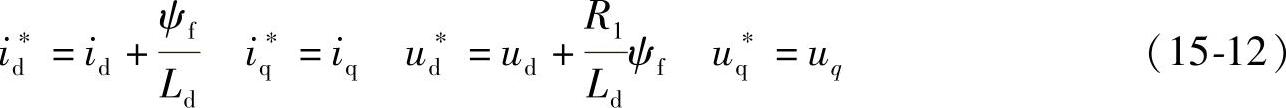
可得

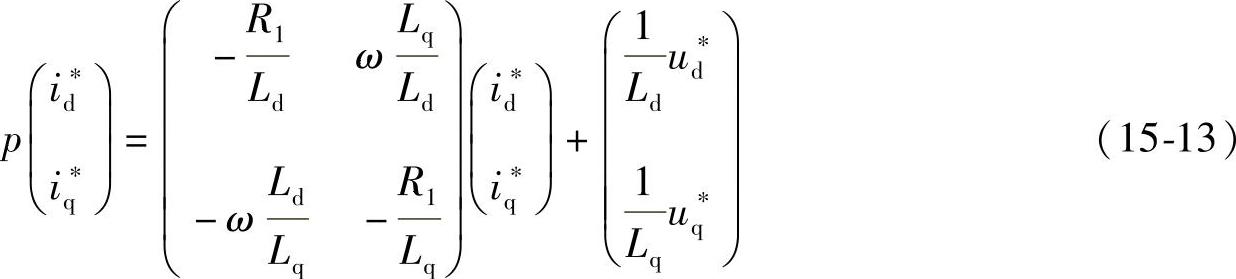
根据电动机的状态方程式15-11，得出以角频率为可调参数的可调模型状态方程如下：

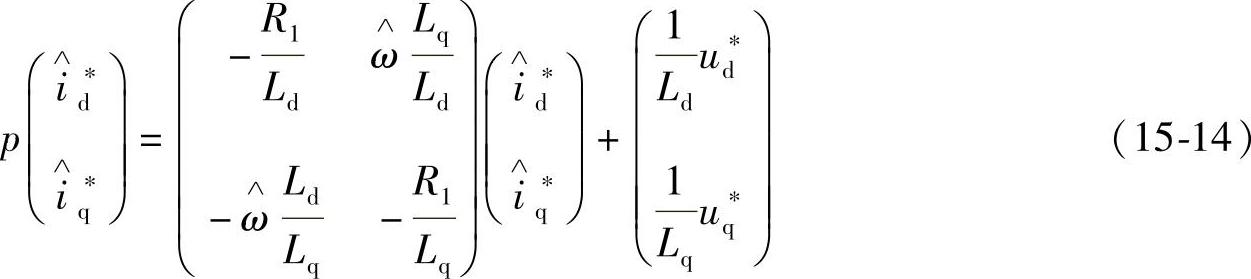
其中

定义广义误差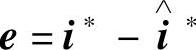，以及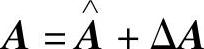，可将式15-13、15-14分别写成如下形式

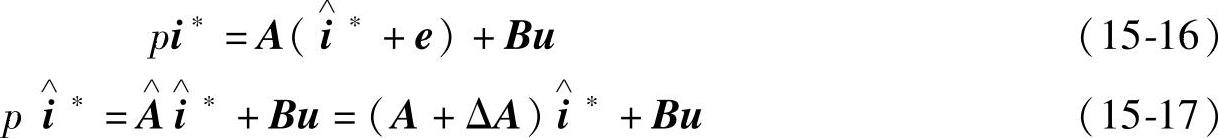
其中：i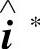^*、分别为定子电流矢量的实际值和估算值，u为定子电压矢量，A、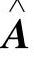、B分别为

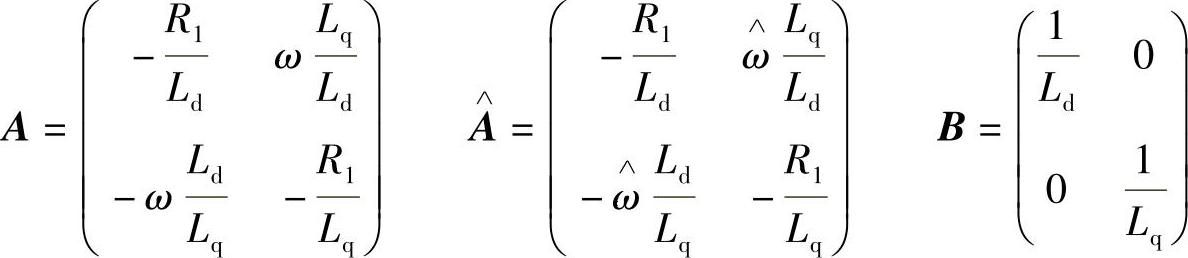
式15-17中ΔA为

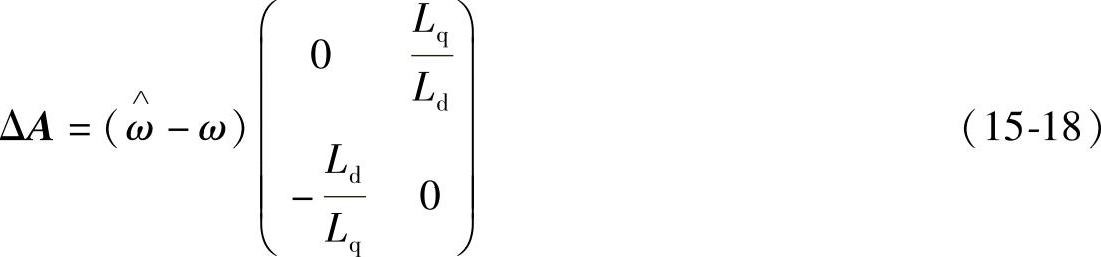
由式15-16、15-17可得

将式15-19化为标准前向环节状态方程为

pe=Ae-Iw

v=Ce （15-20）

式中，，。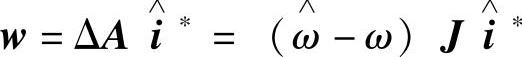

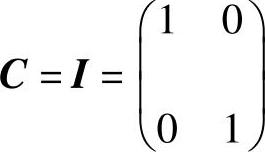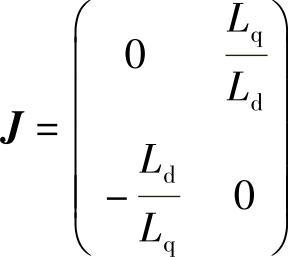以电动机本体为参考模型，根据式15-20构建的基于MRAS的永磁同步电动机矢量控制系统框图如图15-1所示。

根据POPOV超稳定性定理，要使式15-20误差系统稳定，必须同时满足以下两个条件：

1）该系统的传递函数矩阵G（s）=C（sI-A）^-1正定

将A、C代入G（s），可得

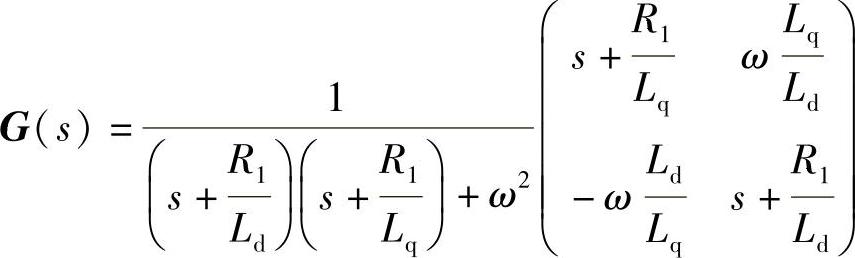
易得G（s）正定。(https://www.xing528.com)

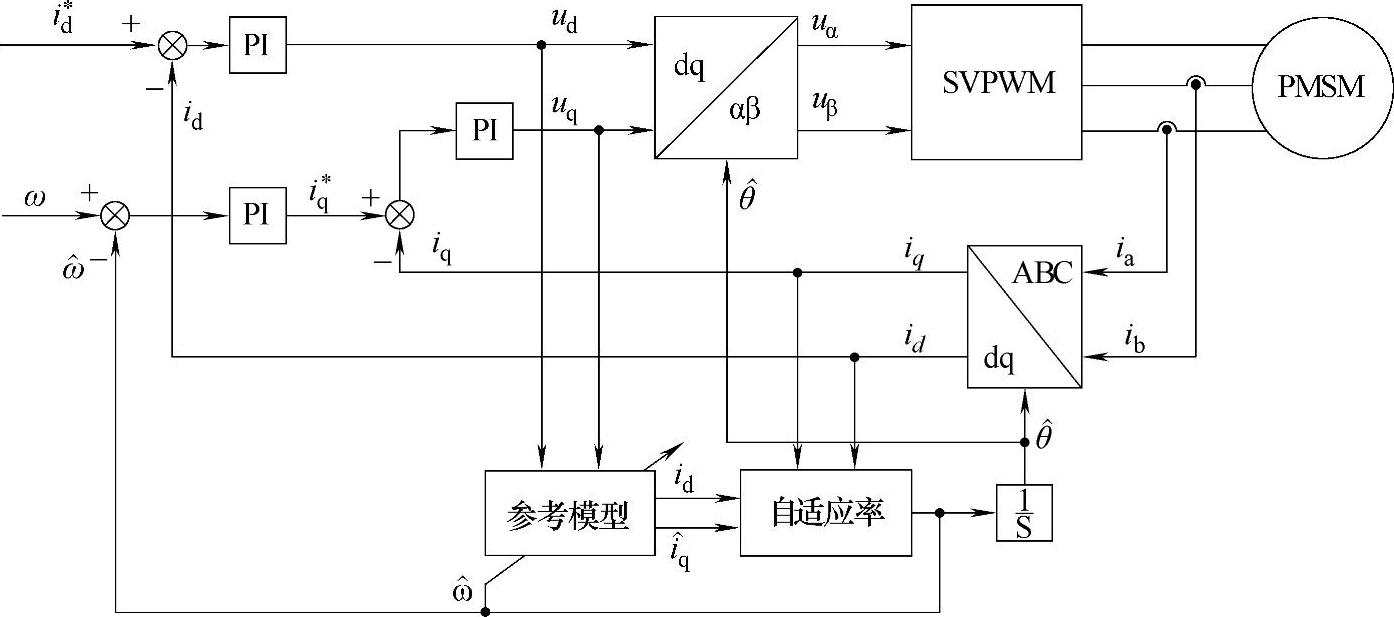
图15-1 基于MRAS的PMSM矢量控制系统框图

2）非线性时不变环节要满足Popov积分不等式

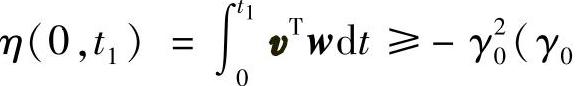是一个有限正常数，且不依赖于t₁）

将v，w代入积分不等式，可得

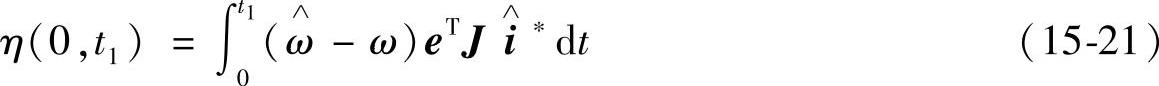
记函数f（t）满足下式

取F₁与F₂为

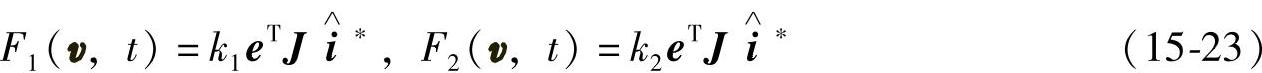
并取电动机转速的自适应调节律为如下的比例积分形式为

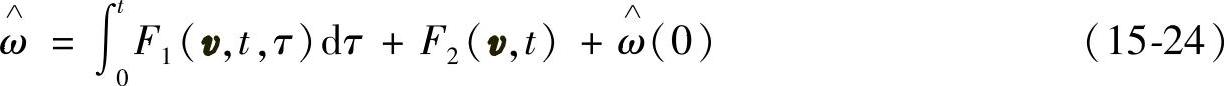
将式15-24代入式15-21，可得

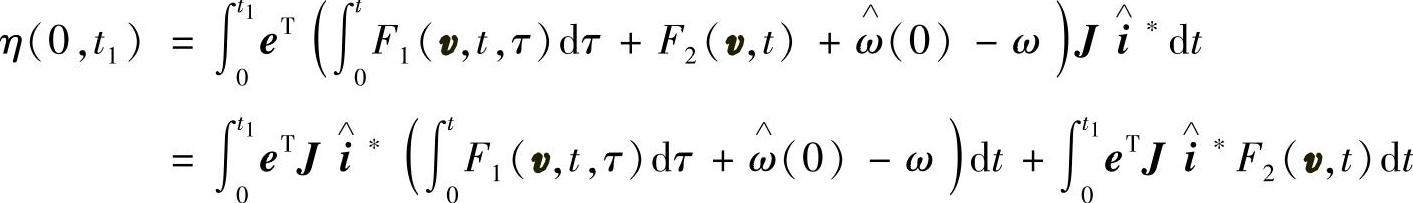
令_η=η₁+η₂，则有

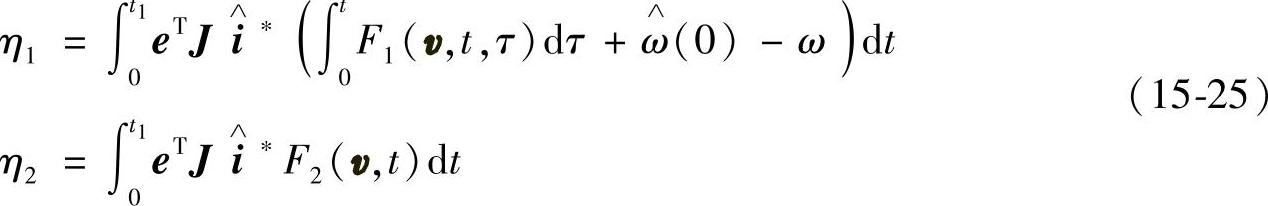
取下式

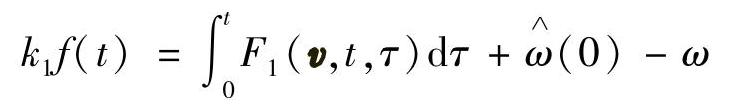
由不等式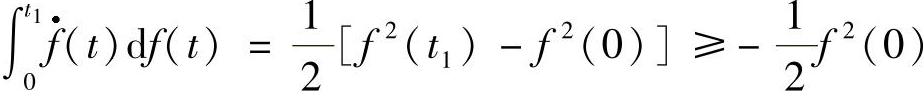，可知，

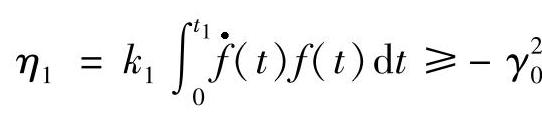
另有

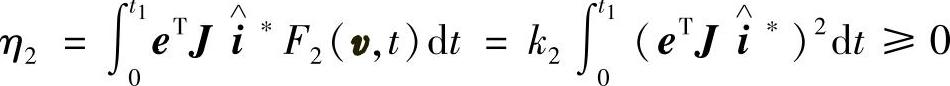
综上可得

η≥-γ²₀ （15-26）故该误差系统是稳定的。

将式15-23代入式15-24，可得电动机转速的自适应律为

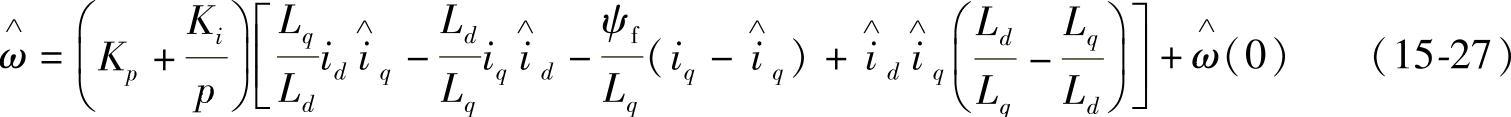
式15-27中的p是微分算子。

MRAS的速度观测是以参考模型的准确为前提的，它直接影响到速度辨识及整个控制系统的工作成效，所以如何尽量减少电动机物理参数的变化对参考模型的影响，是MRAS辨识方法需要进一步解决的问题；同时MRAS方法目标是使控制系统对控制对象参数变化不敏感，以及对未建模部分的动态过程不敏感。当对象处于动态变化时，系统将试图马上感受这一变化并实时调节控制器参数或控制策略，所以控制系统中自适应算法的参数选取非常重要。

在模型参考自适应算法中，由于缺乏对测量误差和系统噪声等不确定因素的校正机制，使得这种方法对系统参数的依赖性比较强。