PMSM转矩脉动分析：传统直接转矩控制的优化

从式13-17、13-18和13-19可以看出：电磁转矩变化量的前两个分量ΔT_e1与ΔT_e2均为负值，并且它们只与电动机前一时刻的磁链、转矩及电动机的速度有关。只有ΔT_e3项可能为正，而它与u_1，k+1密切相关——通过选取具有适当幅值和相角的u_1，k+1可以使电动机产生预期的转矩响应。但是传统直接转矩控制中的电压矢量表仅由少量的电压矢量构成（例如两电平电压型逆变器只有8个），其大小与幅值都是恒定不变的；再者，从电压矢量表中查询到某个合适的电压矢量后，该电压矢量将在电动机定子上作用T_s时间。故而ΔT_e3的大小是难以控制的，这必然导致较大的转矩脉动。特别是低速时电动机需要的电压较低，通过查询矢量表得到的较大幅值的电压矢量会使转矩有很大的变化量，这就导致了稳态时转速有较明显的波动，极大地恶化了低速下电动机的控制性能。

图13-9 定子磁链瞬时旋转角速度示意图

式13-8和13-9分别给出了非零电压矢量与零电压矢量作用在电动机定子后，定子磁链的瞬时旋转角速度。在传统直接转矩控制（Classical Direct Torque Control，CDTC）技术中，这两类电压矢量是交替作用在电动机定子上的。图13-9给出了电动机工作在不同速度时，定子电压矢量对定子磁链瞬时旋转角速度作用的示意图，图13-10则给出了对应的电动机转矩脉动示意图。

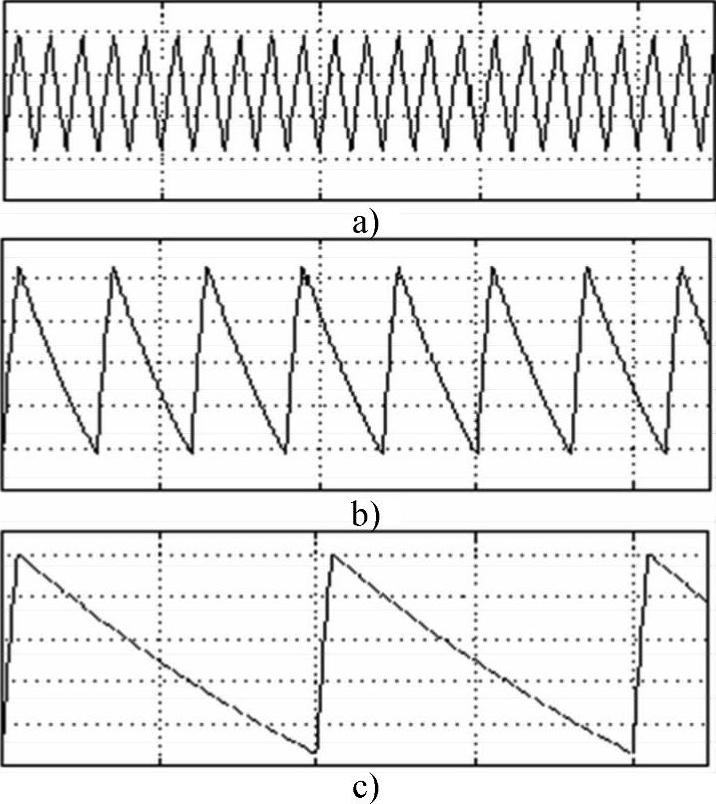
图13-10 电动机电磁转矩脉动示意图(www.xing528.com)

图13-9a、图13-9b、图13-9c分别对应了电动机转速逐渐减小的工况。当电动机运行于稳态情况下，定子磁链旋转的平均角速度总是与电动机转子的电角速度是相等的。图13-9a中的ω_Ψ1与ω_Ψ0交替出现，那么平均角速度约为。此时电动机的转矩以较快的速度交替上升与下降，总的说来，此时的转矩脉动较小，见图13-10a。

图13-9b中交流电动机的速度大约为0.167ω_Ψ1。根据前面的分析可知，由于电动机转子旋转速度较小，所以施加非零电压矢量时，与图13-9a相比，定、转子磁链之间的夹角在相同的时间（T_s）内会增加更多一些，因此电动机的转矩就会更加快速地增加。所以电动机的转矩在一个T_s内就有了较大的增加，如图13-10b，因而转矩砰砰控制器决定了在下一个T_s范围内定子电压矢量改选为零电压矢量。此时定子磁链矢量基本不动，而由于电动机的转速较小，定转子磁链之间夹角的减小速度较图13-9a慢一些，所以转矩以较小的速度减小。在等到电动机的转矩减小到滞环调节器的下限过程中，图13-9b中已经插入了比13-9a更多的零电压矢量。与图13-10a相比，图13-10b中的转矩脉动已经有较大的增加。

再分析图13-9，由于此时电动机的运行速度已经很低，约为，一个控制周期T_s内非零电压矢量的作用就已经导致电动机的转矩有了特别大的增加，远远超出了误差带。所以接下来需要更多个周期的ω_Ψ0（采用零电压矢量）才能使电动机的转矩回落到误差带范围内，随后又是一个循环。从整体上看，转矩也能围绕着负载转矩上下变动。但从局部细节看，定子磁链旋转速度时而过大，导致转矩有过大的增加；时而很小，并且长时间采用零矢量，致使定子磁链幅值会有较大程度的减少，增加了电流中的谐波分量。电动机转矩的脉动经过较大惯性的机械系统的衰减后变为电动机转速的波动。但过大的转矩脉动就会使得电动机产生明显的振动，这对于生产机械来说极为不利，也恶化了调速系统运行的稳定性，这就是CDTC的一个较明显的缺点。

从上面的分析中可以看出：传统直接转矩控制技术中，所需的定子磁链角速度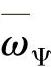是要通过若干个T_s才能实现的，并且也只能是一些不连续的值（所以定子电流频谱的谐波分布比较宽）；而磁场定向矢量控制技术采用了成熟的SVPWM等脉宽调制技术，能够在一个Ts内产生所需的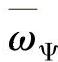，所以能够在短时间内产生与负载相平衡的转矩，因此稳定了转速。这一点是CDTC方案性能改进的基础。