PMSM转矩增量分析的优化方法

下面首先根据转子坐标系中永磁同步电动机的数学模型推导出在一个数字控制周期Ts内转矩的增量ΔT_e（假定L_d=L_q）。

dq转子坐标系中PMSM定子电压矢量方程式为

u₁=R₁i₁+pΨ₁+jωΨ₁ （13-11）

而定子电流矢量可以表示为

那么在一个控制周期T_s内，施加在电动机定子上的电压矢量u₁，k+1产生的新的定子磁链矢量为

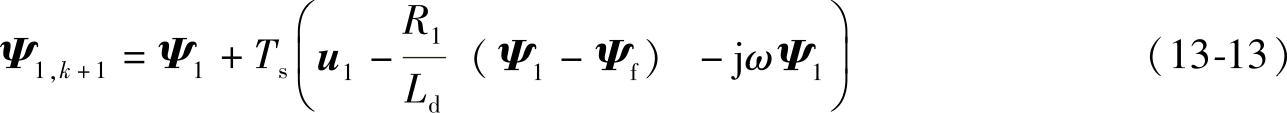
电动机的转矩可以描述为

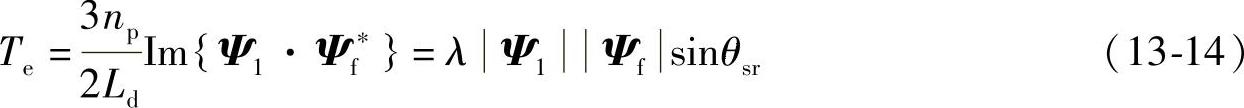
上式中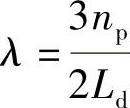，Im{}表示取复数的虚部。根据式（13-14）可以求出在（k+1）Ts时刻的电动机转矩T_e，k+1为

T_e，k+1=λIm{Ψ_1，k+1·Ψ^*_f，k+1} （13-15）

将式（13-13）代入式（13-15），一般T_s较小，忽略T_s的高次项后得到

T_e，k+1≈T_e，k+ΔT_e1+ΔT_e2+ΔT_e3 （13-16）

其中T_e，k=λIm{Ψ_1，k·Ψ^*_f，k}，表示kT_s时刻电动机的电磁转矩。这样可以得到电动机转矩的增量ΔT_e，它由下面三部分组成：

ΔT_e1=-T_s·T_e，k/T₁ （13-17）(www.xing528.com)

ΔT_e2=-T_sωT_e，kcosθ_sr/sinθ_sr （13-18）

ΔT_e3=λT_sψ_fu_1q=λT_s∣ψ_f，k∣·∣u_1，k+1∣·sinγ （13-19）

上式中：T₁=L_d/R₁，角γ是施加在永磁电动机定子端的电压矢量u_1，k+1超前当前转子磁链矢量ψ_f，k的电角度。电动状态下，前两项转矩增量为负，只有第三项在合适的u_1，k+1下才可能为正。

综上所述，在一个控制周期T_s内电动机转矩增量ΔT_e的三个组成部分与电动机自身的参数、转子磁链的幅值、电动机在前一时刻的转矩、转子的速度、数字控制系统的控制周期以及定子电压矢量有关，见表13-4。

表13-4 影响电动机电磁转矩变化的各种因素

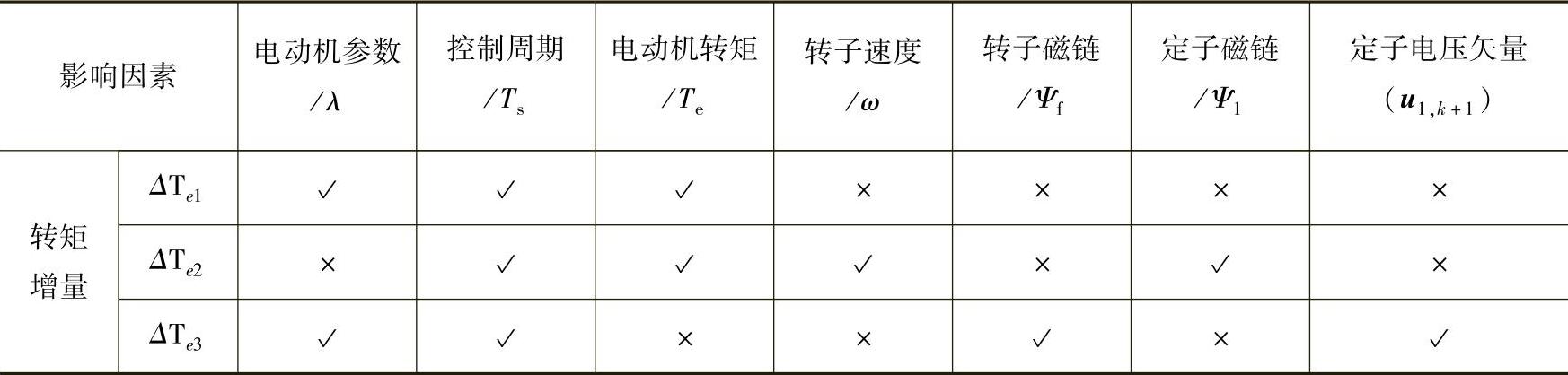
注：表中的√表示该因素对转矩增量有显著影响，×表示它对转矩变化量基本没有影响。

使用表13-4可以对电动机转矩控制性能进行较详细的分析：

1）ΔT_e1、ΔT_e3增量与电动机参数λ有关，因此可以通过设计或选取具有合适参数的电动机使调速系统获得较好的转矩性能指标。

2）三项转矩增量均与采样时间T_s成正比，因此通过减小采样时间可以减小转矩的脉动，从而对其实施更精确的控制。但这无疑对数字控制器的运算速度提出了更高的要求。同时T_s的选取还与系统数字控制器的运算量有关，不能一味地通过减小T_s提高转矩的控制性能。

3）kT_s时刻的电磁转矩与两项负的增量有关系。

4）转子速度对后两项有影响。ΔT_e2以与转速成正比的速度下降；在ΔT_e3中，当转子速度较高时，式中的γ不再保持恒定，而有着显著的变化（减少），即这一项正的转矩增量在高速时对转矩增加的贡献不如低速时大。

5）转子磁链对ΔT_e3有明显影响，而定子磁链的选取一方面会影响转矩的变化量ΔT_e2（通过θ_sr起作用），另一方面可以优化系统的运行效率。

6）定子电压矢量直接对ΔT_e3起着重大的控制作用。通过选取不同幅值和相角的u_1，k+1可以产生控制系统预期的转矩响应。