定子磁链控制原理详解

1.基于静止坐标系的定子磁链幅值控制原理分析

永磁同步电动机在静止坐标系的定子电压矢量方程式为

u^2s₁=R₁·i^2s₁+pψ^2s₁ （13-1）

忽略定子电阻的压降，略去右上角的坐标系符号，那么定子磁链矢量可以化简为（从t₀时刻到t₁时刻）：

式13-2表明，当输入电压u₁为零矢量时，即u₁=0，定子磁链矢量保持Ψ₁（t₁）=Ψ₁（t₀）不变；如果u₁是一个非零矢量，那么定子磁链矢量将在原有Ψ₁（t₀）基础上，沿着与输入电压矢量u₁平行的方向，并以正比于u₁幅值的线速度移动。所以在不同时刻，通过选择适当的电压矢量，就可以按照预定的规律（轨迹）对定子磁链进行有效的控制，从而获得旋转的定子磁场。

PMSM变频调速系统中的两电平电压型逆变器输出的基本电压空间矢量在前面已经分析过，如图13-2a所示。显然图13-1中逆变器可以输出到电动机定子端部的电压空间矢量仅仅有8个，不仅数量有限，并且8个电压矢量的幅值和方向也都是固定不变的。

零电压矢量使定子磁链的幅值保持不变，但考虑到定子电阻压降以后，它还是逐渐减小的（相当于电路的零输入响应）。非零电压矢量对定子磁链圆轨迹的控制作用会因定子磁链所处位置不同而变化，下面以U₆矢量为例进行讨论。

首先把两相静止坐标平面360°空间均匀划分为6个扇区（sector），每个扇区为60°，如图13-2b中的S₁～S₆。以定子磁链空间矢量逆时针旋转为正方向，当矢量端点处于图中A点时，在U₆的作用下，定子磁链矢量端点将会向右上角的圆外移动，显然该电压矢量能够使定子磁链幅值增加，同时也使其相角较快地增加。

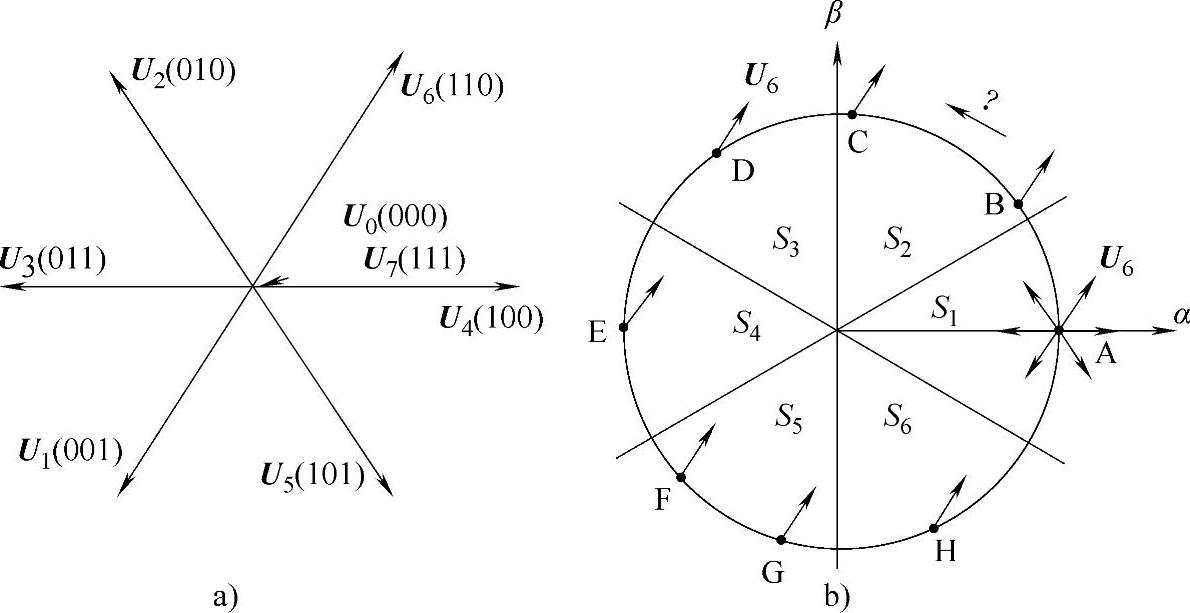
图13-2 两电平电压型逆变器输出的基本电压矢量与空间扇区的划分

当定子磁链分别位于图中A、B、C、D、E、F、G、H时，U₆对定子磁链矢量的作用规律见表13-1。

表13-1 不同位置的定子磁链受电压矢量U₆的影响

表中各符号的含义是：↑↑迅速地增加，↑较快增加，～↑略有增加，↓↓迅速地减小，↓较快地减小，～↓略有减小。

从表13-1可以知道：当定子磁链矢量处于不同位置时，即便是同一个电压空间矢量，它对定子磁链的调节作用也是不相同的，因此对整个空间划分为6个扇区是必要的。考虑到6个非零电压矢量以后，情况就更加复杂了。S₁内各电压矢量对定子磁链矢量的作用见表13-2，其余类推。

表13-2 扇区S₁内各电压矢量对定子磁链的影响

表13-1与13-2中电压矢量对定子磁链幅值的影响可用于定子磁链的闭环自调节，而相角的增加或减小则与电动机的转矩调节相关。

综上所述，要对定子磁链的幅值进行控制，只需要知道它当前所在的扇区以及磁链幅值控制目标（增大还是减小）即可。图13-3给出了采用DTC控制的电动机定子磁链的近似圆形轨迹仿真图。可以看出，在扇区S₁内交替采用U₆与U₂两个电压矢量引导定子磁链矢量端点沿着A→B→C→D→E→F→G路径移动，可以实现定子磁链矢量在空间的正向旋转。

2.基于旋转坐标系的定子磁链幅值控制原理分析

上面的分析是建立在对公式13-2和图13-2的直观理解基础上的，下面根据电动机的数学模型通过相关公式进行分析。

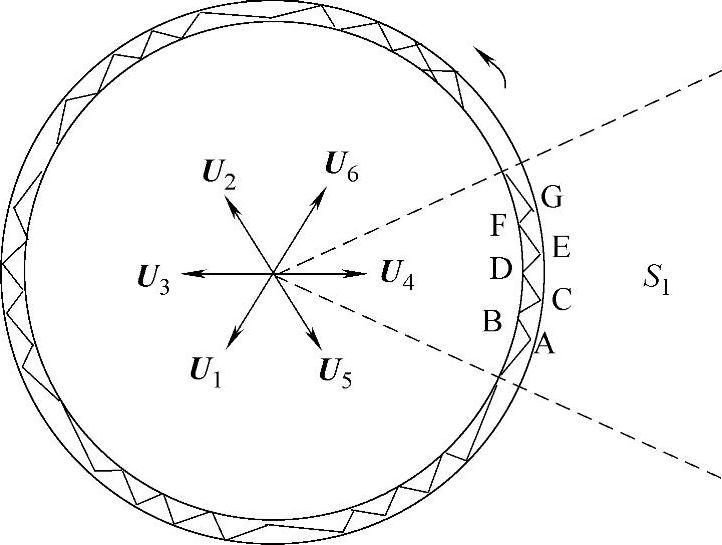
图13-3 电压空间矢量对磁链轨迹的控制作用仿真图

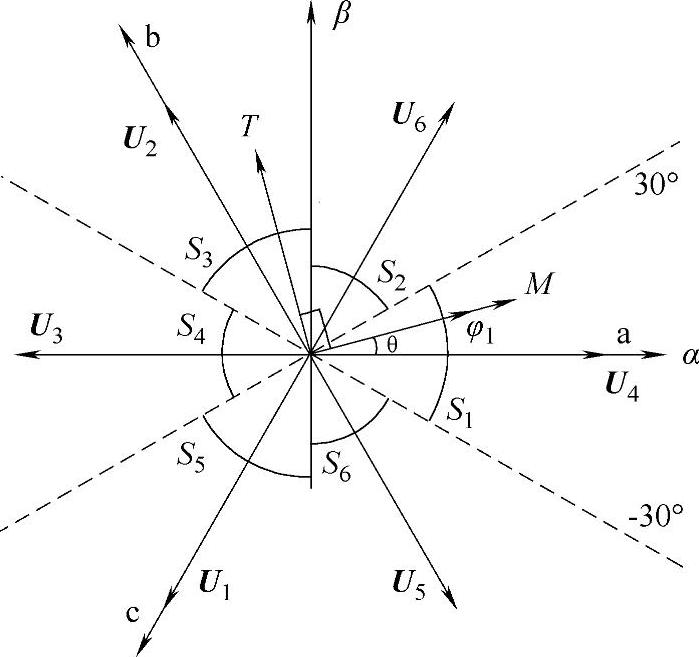
图13-4 MT坐标系以及空间扇区示意图

建立在以定子磁链矢量定位的同步旋转坐标系（这里称为MT坐标系，见图13-4）中永磁同步电动机定子电压方程式的矢量形式为

u₁=R₁i₁+pψ₁+jω₁ψ₁ （13-3）

上式中ω₁为定子磁场坐标系的同步速度，将其改写为标量方程为

u_M=R₁i_M+pψ_M-ω₁ψ_T

u_T=R₁i_T+pψ_T+ω₁ψ_M （13-4）(www.xing528.com)

由于该MT坐标系是采用定子磁链矢量进行定位（M轴与定子磁链矢量方向重合），所以下述关系式成立：

ψ_M=ψ₁

ψ_T=0 （13-5）

从而定子电压方程变为

u_M=R₁i_M+pψ₁

u_T=R₁i_T+ω₁ψ₁ （13-6）

式13-6中的u_M和u_T是电压型逆变器输出电压空间矢量在M、T坐标轴上的分量。当定子磁链空间矢量在空间内旋转时，各电压矢量的u_M和u_T分量就会随θ变化而变化。图13-5给出了u_M和u_T在扇区S₁中随θ（M轴与A轴的夹角）的变化情况。图中的U_m=2U_d/3=|U_i|为非零电压矢量的幅值（i=1～6）。

重新列出M轴电压方程式u_M=R₁i_M+pψ₁，由于定子绕组电阻一般都很小（大功率电机更是如此），可近似改写为

u_M≈pψ₁ （13-7）

这就表明了电动机定子磁链的幅值ψ₁直接受到u_M的控制，正的u_M分量会增加ψ₁；负的u_M分量会减小ψ₁。参考图13-5可以知道，扇区S₁内各电压矢量对定子磁链幅值的控制作用见表13-3。

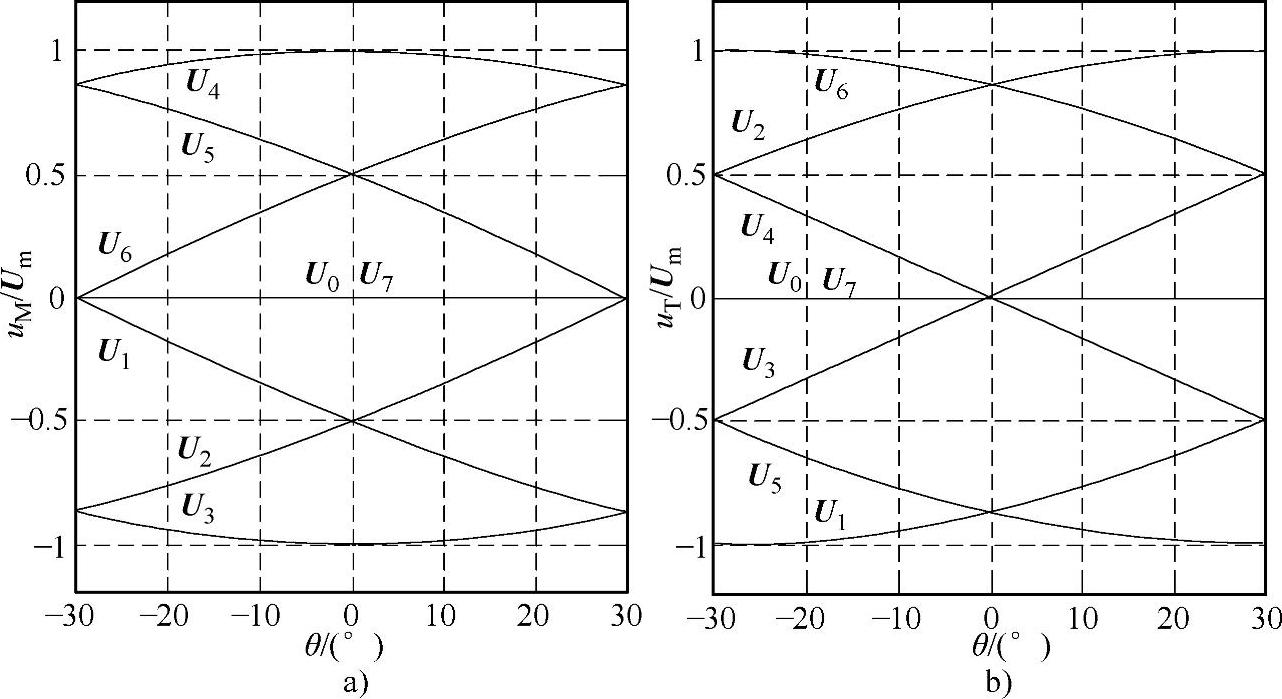
图13-5 扇区S₁内u_M、u_T变化规律

表13-3 扇区S₁中各电压矢量对定子磁链幅值作用表

其中U₁、U₂可以减小ψ_M，U₅、U₆则增加ψ₁；而U₃急剧减小ψ₁，U₄则急剧增加磁链ψ₁；U₀、U₇保持ψ₁基本不变。该表格的内容与表13-2相符。

综上所述，当定子磁链矢量位于扇区S₁内时，若对其幅值进行控制，那么定子电压矢量的选择原则为：

1）若需要迅速建立磁场，可以选择U₄（有可能会引起电流的冲击）。

2）若需要迅速减小磁场，可以选择U₃（有可能会引起电流的冲击）。

3）若要保持磁场基本不变，可以选择零电压矢量U₀或U₇。考虑到定子电阻的存在，实际的ψ₁会逐渐衰减的。

4）若需要小幅度增加磁场，可以选择U₅或U₆。同时从图13-5中还可以看出它们对磁场的影响还是有区别的：U₅在前30°范围内的作用比较强，而在后30°范围内的作用比较弱；U₆则正相反。值得注意的是：如果在-30°附近时选择U₁或者U₆的话，考虑到定子电阻的存在，那么就可能出现电压矢量对ψ₁的控制达不到预期控制效果的情况。

5）若需要小幅度减小磁场，可以选择U₁或U₂。这时它们也存在前述的情况：电压矢量的实际控制效果会随着定子磁链矢量的位置有所变化。

在其余各扇区内，定子电压矢量对电动机定子磁链幅值的控制作用可以依次类推。

3.定子磁链相角的控制原理分析

前面对式13-2的分析中指出：当定子输入电压为零矢量时，定子磁链矢量就保持不变；如果是一个非零电压矢量作用，定子磁链矢量端点将在原有基础上，沿着与输入电压矢量u₁平行的方向，以正比于u₁幅值的速度移动。式13-2表明定子磁链矢量端点移动的线速度就是定子电压矢量的幅值：vΨ=∣u₁∣。对于非零电压矢量：vΨ1=2U_d/3；对于零电压矢量，有v_Ψ0=0。非零定子电压矢量作用下定子磁链的瞬时旋转角速度为

ω_Ψ1=2U_d/（3∣Ψ₁∣） （13-8）

零电压矢量作用下，定子磁链瞬时旋转角速度为

ω_Ψ0=0 （13-9）

图13-4中逆变器输出的非零电压矢量的幅值都很大，所以一旦选择其中一个矢量，那么定子磁链的瞬时旋转角速度将是很大的；若采用零电压矢量，瞬时旋转角速度就为零。

表13-2给出了扇区S₁内各非零电压矢量对定子磁链矢量相位角的控制作用，其余扇区可以依次类推。在定子磁链幅值没有较大的变化时，定子磁链相角的增加和减小是与交流电机定子、转子磁链矢量夹角的增大和减小是相对应的。表中U₃、U₄一般不用，它们会导致定子磁链幅值的显著变化，破坏了电动机转矩控制的前提，除非当定子磁链显著偏离给定值需要对其迅速调节。另外，零电压矢量U₀、U₇作用时，虽然磁链相角基本不变，但是在电动机转子转动的情况下，电动机的转矩角会减小。