FOC控制系统中的dq坐标系电流闭环PI调节优化

目前，最为常见的永磁同步电动机FOC控制系统如图12-3所示。系统有一个转速外环，通过速度自动调节器（ASR）提供i_q的指令值，i_d指令值通过其他方式提供（例如根据电动机弱磁程度）。两个电流指令值分别通过经典的PI调节器获得dq轴控制电压u_dref与u_qref，将电压变换到αβ静止坐标系后采用SVPWM技术控制电压型逆变器向PMSM供电。

如图12-3所示控制系统中的电压型逆变器、SVPWM、各个坐标变换单元在前面章节已经介绍和分析过，这里着重对图中的3个PI调节器进行分析。

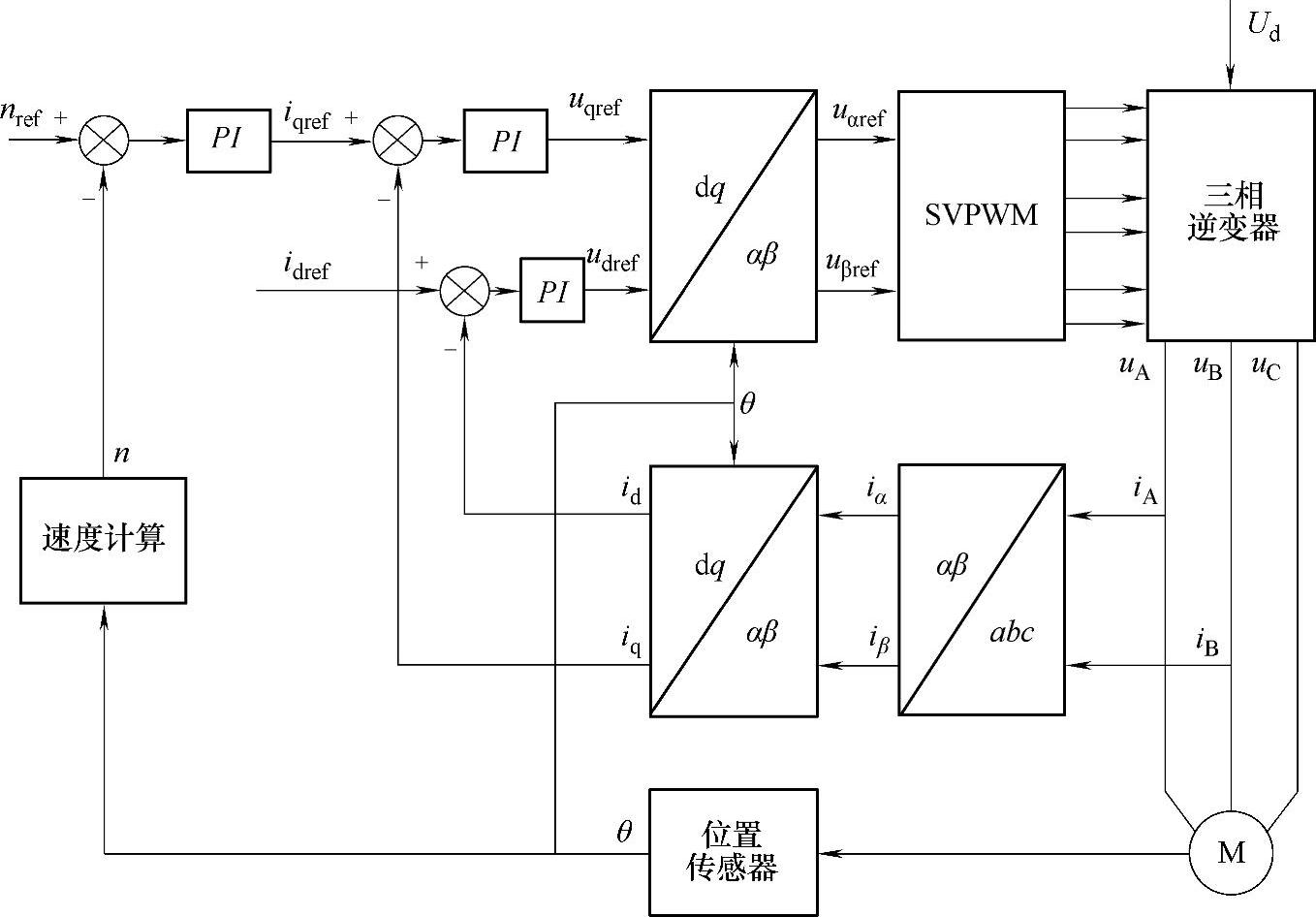
图12-3 永磁同步电动机矢量控制系统结构框图

PI调节器的数学表达式见式12-3，其对数幅频特性曲线如图12-4所示。可以看出，在较高频段（对应了系统的快速调节过程）的放大倍数主要决定于K_p，这是因为积分器呈现低通特性；在较低频段（对应了系统进入稳态后的缓慢调节阶段）的放大倍数与K_i密切相关（不同频率与K_i的关系程度不同）。

图12-5分别给出了恒定的K_p、K_i、τ下的PI调节器对数幅频特性曲线的变化情况。从中可以看出：

1）当K_p恒定时，若K_i增加，则时间常数减小。低频范围内响应加快，中频段有所加快，高频范围内没有明显影响。

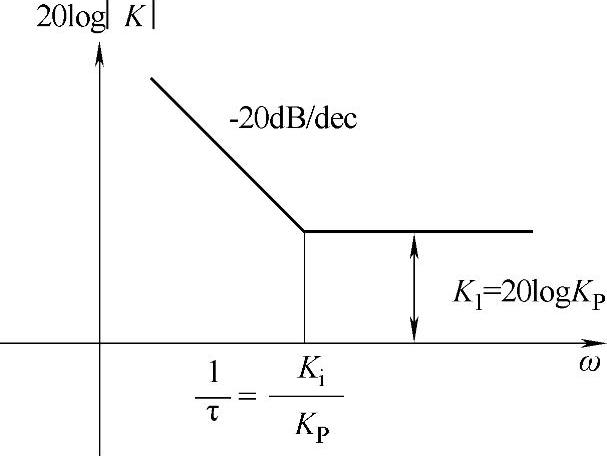
图12-4 PI调节器的对数幅频特性

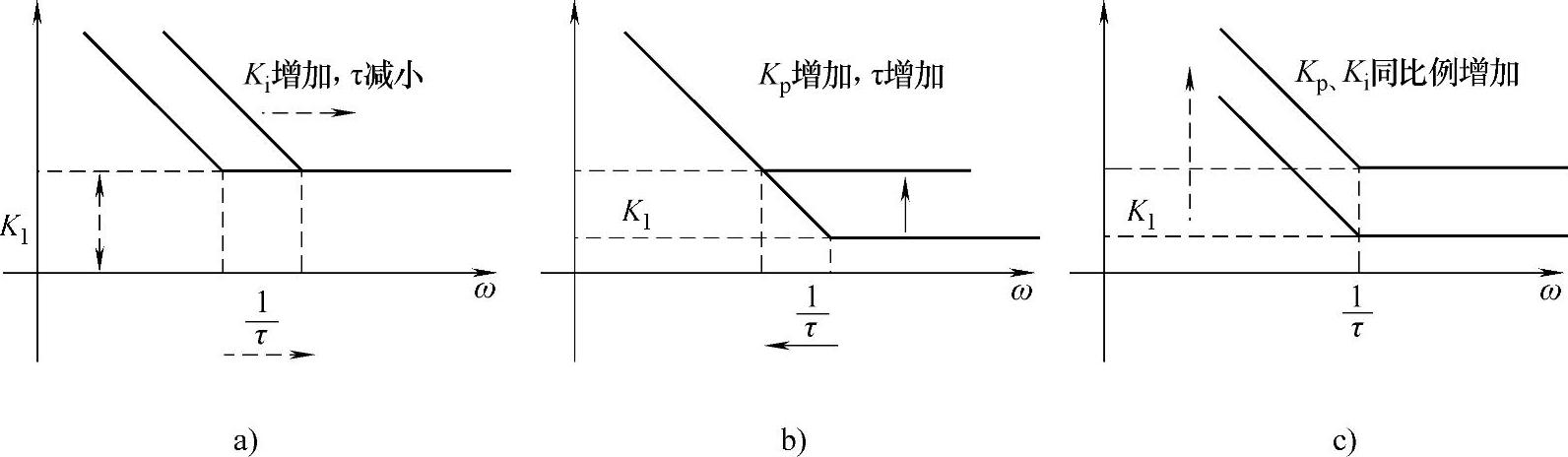
图12-5 不同调节器参数对PI调节器幅频特性的影响

a）K_p恒定 b）K_i恒定 c）τ恒定

2）当K_i恒定时，若K_p增加，则时间常数增加。高频范围内响应明显加快，中频段也有所加快。

3）当时间常数恒定时，K_p与K_i同比例变化。按照时间常数对调节器参数进行调节，可以比较明确地调节系统的转折频率。

技术人员通常会尝试增加K_p来加快系统响应速度。从图12-5中可以看出，这将直接增大图中的K₁，从而导致调节器幅频特性上移，明显可以增加系统的调节力度，系统的响应会因此加快；但由于高频段的特性同样会上移，所以会导致闭环系统对高频干扰的响应过于敏感，不利于系统的稳定。

换句话说，如果希望提高闭环系统对高频的响应，需要适当加大K_p；如果希望提高闭环系统对低频的响应，可以适当加大K_i；如果希望闭环系统对较高频率信号不敏感，可以选择适当的时间常数τ。

以MATLAB/SIMULINK为例，在建立PI调节器仿真模型时，可以采用图12-6中的两种不同结构，读者可以根据分析与调试的方便选择其一。注意图中饱和限幅（Saturation）值需要进行合理的设定。以ASR为例，由于通常情况下调速系统往往设计成稳态无静差，并且ASR的输出为i_q指令，所以积分器限幅与ASR的输出限幅应设为允许的i_q最大值。

图12-6 两种PI调节器仿真模型

下面针对图12-3的PMSM矢量控制系统中的PI调节器采用工程化设计方法进行参数设计。首先画出图12-7所示的PMSM矢量控制变频调速系统动态结构框图，在其中加入了转速滤波和电流滤波等环节，并忽略了i_d的控制回路（假定i_d是恒定值），其中的ASR与ACR都采用PI调节器。u_c作为ACR调节器的输出，用来控制逆变器输出电压u_q，逆变器等效为图中所示的放大系数为K_s的一阶惯性环节。K_te表示电动机的转矩系数，见式12-4。

图12-7 中的T_m为电动机的机械时间常数，见式12-5。

图12-7 中的K_e为电动机的反电动势系数，满足下式。

图12-7所示变频调速系统动态结构图中包含了两个闭环控制，一个是转速的外环控制，另一个是电流的内环控制。对调速系统的转速、电流闭环调节器参数进行工程设计，可以遵循下述步骤：

1）用工程设计方法来设计转速、电流反馈控制的调速系统的原则是先设计内环再设计外环。

2）先从电流环开始，对其进行必要的变换和近似处理，然后根据电流环的控制要求确定其校正目标。

3）再按照控制对象确定电流调节器的类型，按动态性能指标要求确定电流调节器的参数。

4）电流环设计完成后，把电流环等效成转速环（外环）中的一个环节，再用同样的方法设计转速环。

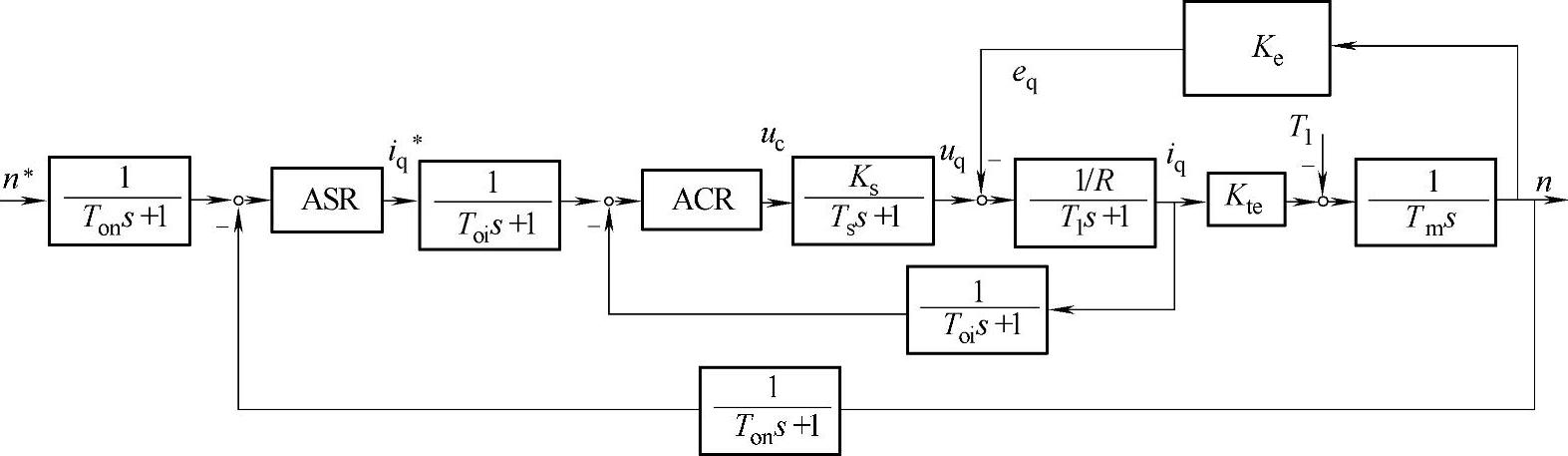
图12-7 PMSM矢量控制变频调速系统动态结构框图

1.电流调节器设计

从图12-7中可以看出，电动机反电动势与电流反馈的作用相互交叉，给设计工作带来麻烦。但是实际的电动机调速系统中由于较大的机械惯性，转速的变化往往比电流变化慢得多，对电流环来说，反电动势是一个变化较慢的扰动，在按动态性能设计电流环时，可以暂不考虑反电动势变化的动态影响。

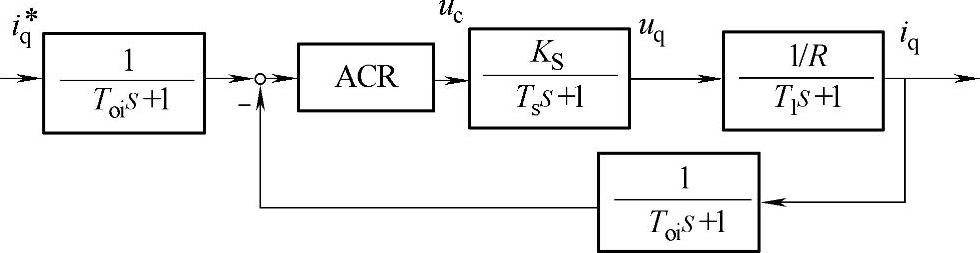
图12-8 忽略反电动势后的电流调节内环结构图

图12-8给出了忽略q轴电动机反电动势作用后的电流调节内环的结构图。

忽略反电动势对电流环作用的近似条件是：

上式中的ω_ci是电流环开环频率特性的截止频率。

将图12-8进行等效变换，得到图12-9的结构图。图中除了ACR调节器外，还有3个惯性环节，其中的时间常数T_oi、T_s比T₁小得多，可以当做小惯性环节近似处理成图12-10所示的结构图。需要注意的是，近似处理需要满足式12-8。

图12-9 等效后的电流调节内环结构图

图12-10中的时间常数T∑i见式（12-9）。

T_∑i=T_oi+T_s （12-9）

在电流环的设计中，一般希望稳态情况下，电流调节无静差，并且能够较好地跟随电流指令值。在强调跟随性能下可以把电流环设计成如图12-11所示的典型Ⅰ型系统。

图12-10 近似处理后的电流环结构图

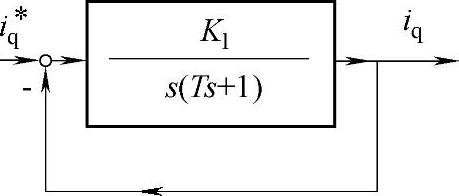
图12-11 典型Ⅰ型系统结构图

对比图12-11与图12-10可知，电流调节器可以采用PI调节器，其传递函数为(www.xing528.com)

因为T₁＞＞T_∑i，所以选择

τ_ACR=T₁ （12-11）

可以用PI调节器的零点消去控制对象中较大时间常数对应的极点。一般情况下，希望电流超调量不要太大，通常选取阻尼系数为0.707，此时图12-11的系统有

T=T_∑iK₁T_∑i=0.5 （12-12）

对比图12-11与图12-10，有

所以有

经过上述的PI调节器参数设计后，电流内环的闭环传递函数为

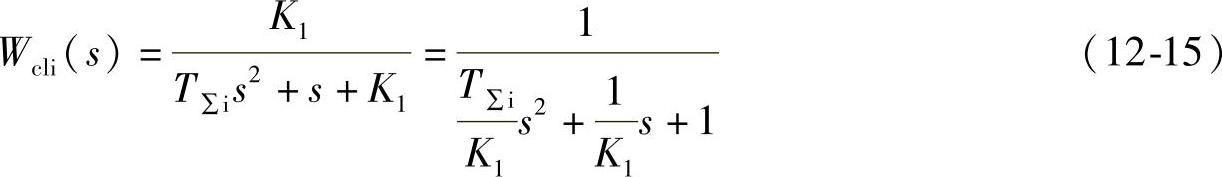
采用高阶系统的降阶处理方法，忽略高次项，式（12-15）可以近似为

近似的条件为

此时，电流控制内环结构图可以等效为如图12-12的结构图。

可以看出，电流的闭环控制把双惯性环节的电流环控制对象近似地等效成只有较小时间常数的一阶惯性环节，加快了电流的跟随作用，这是局部闭环（内环）控制的一个重要功能。

需要注意的是，电流调节器参数设计后，要对以下条件是否成立进行校验：忽略反电动势变化对电流环动态影响的条件（式12—7）；电流环小时间常数近似处理条件（式12-8）。

2.转速调节器设计

将电流环简化等效环节放入到图12—7的系统动态结构图后得到图12 -13的动态结构图。

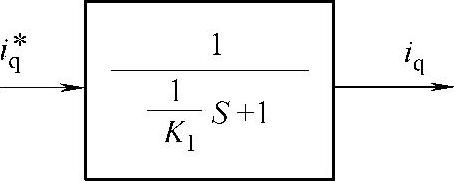
图12-12 简化等效后的电流环

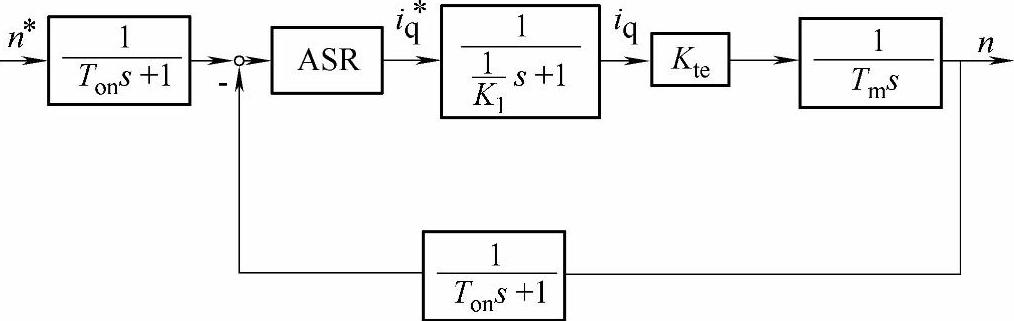
图12-13 代入电流环简化环节的转速环结构图

将图12-13中的滤波环节移入到前向通道上，得到图12-14所示的结构图。

图12-14 具有单位负反馈的转速环结构图

将图12-14中两个惯性环节合并成为一个，图12-14的系统可以近似处理成图12-15的系统，其中T_∑n见式（12-18）。

转速环小时间常数合并处理的条件是：

在转速环的设计中，一般希望稳态情况下，转速调节无静差，并且具有较好的抗干扰能力，因此可以将转速环设计成典型Ⅱ型系统，图12-16给出了典型II型系统的动态结构图。

图12-15 近似处理后的转速环结构图

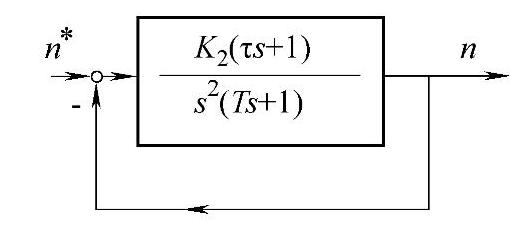
图12-16 典型Ⅱ型系统结构图

对比图12-16与图12-15可知，ASR转速调节器可以采用PI调节器，其传递函数如下：

图12-16中系统的参数如下：

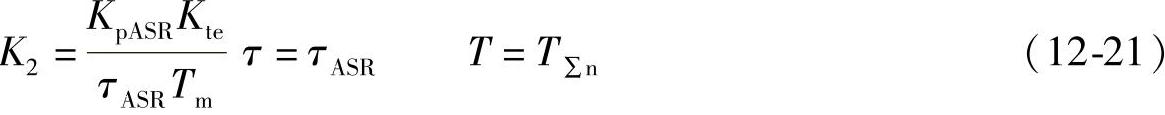
通常情况下，针对Ⅱ型的转速环，综合考虑跟随性能指标与抗扰性能指标，可以选取中频宽h=5，即

根据式（12-22）可计算出ASR的时间常数τ_ASR。

根据“振荡指标法”中闭环幅频特性峰值最小准则，可以得出下式：

从而可以计算出ASR的比例系数K_pASR。

需要注意的是，转速调节器参数设计后，要对以下条件是否成立进行校验：电流环简化条件（式12-17）；转速环小时间常数近似处理条件（式12-19）。

图12-17将电流内环与转速外环的开环对数幅频特性进行了比较，可以发现：外环的响应要比内环更慢，这是设计多环控制系统的特点；需要注意的是，两个闭环控制的剪切频率要间隔一定的距离以避免两个闭环调节相互影响。

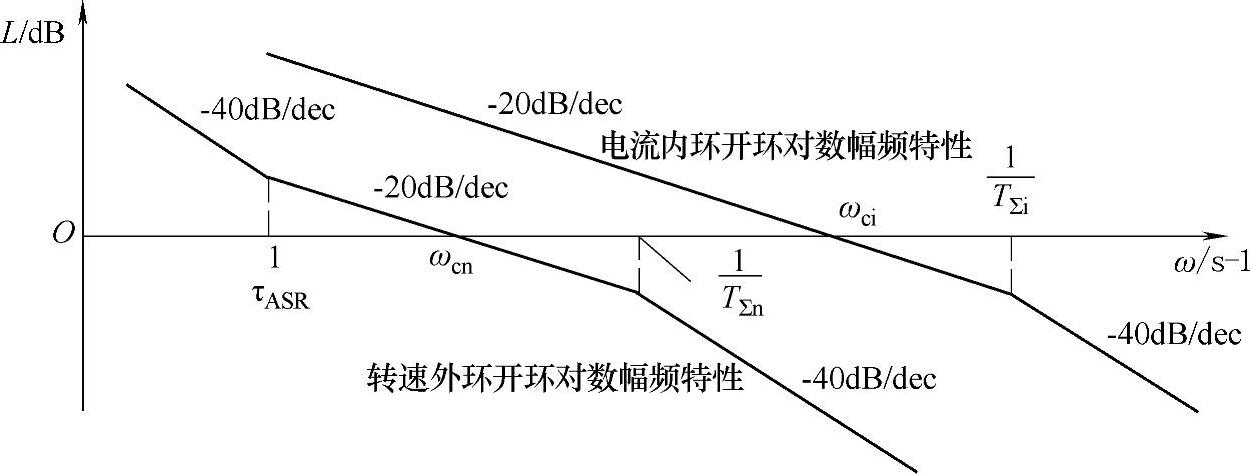
图12-17 电流内环、转速外环开环对数幅频特性的比较