LC电路滤波器由图10-9中的L1与C1共同构成，为推导逆变器直流侧电流id在电网侧产生的电流iL，可以将供电系统直流电压源进行短路，如图10-9中虚线所示，图中的电阻RL为供电电路的等效串联电阻，RC为电容器等效串联电阻。
图10-9中的电容器C1有
sUc（s）-Uc（0）=Ic（s）/C1
图中的电感器L1有
sIL（s）-IL（0）=UL（s）/L1
所以有
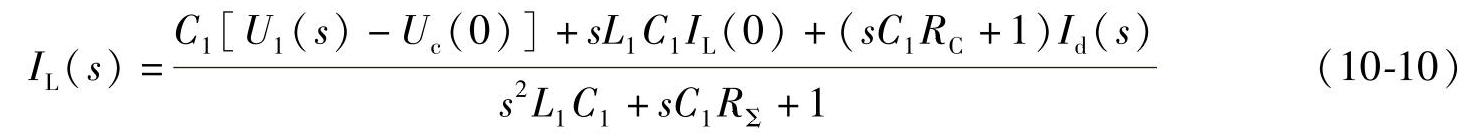
上式中，RΣ=RL+RC，它是LC滤波器回路的等效串联电阻。
当逆变器直流侧电流id中含有直流分量与谐波分量时，可以根据式（10-10）分别求出相应的iL。对于线性电路，可以采用叠加定律对各激励产生的响应分别计算后叠加得到总的响应。这里不考虑电容器和电感器的初始状态产生的响应，因此iL为
其中，id中直流分量的频域表达式为Id（s）=Idc/s，它产生的iL响应为
(www.xing528.com)
借助MATLAB工具进行拉氏反变换后，可以得到式10-13的时域表达式为
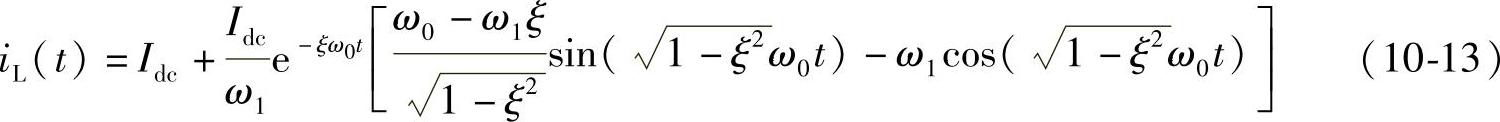
式（10-13）中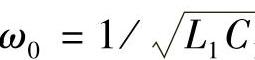
，
，
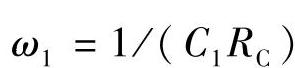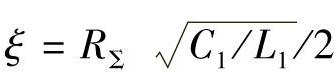。从该式可以看出：iL（t）的稳态分量刚好等于Idc，这说明电动机与逆变器系统需要的直流电流全部从电感器经过，换句话说，这个直流分量全部由电网提供。另外从该式中还可以看出，id直流分量会激发出LC滤波器的固有振荡分量，该分量在暂态过程中出现，然后逐渐衰减到0。如果系统的阻尼系数和无阻尼振荡频率过于小，那么时间常数1/（ξω0）就会很大。逆变器直流侧电流id中的频率为ω的正弦电流i1的时域表达式为：
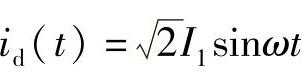，其频域表达式为
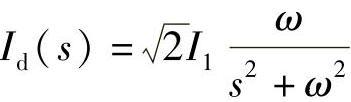。可以推导出i1产生的电流iL频域响应为
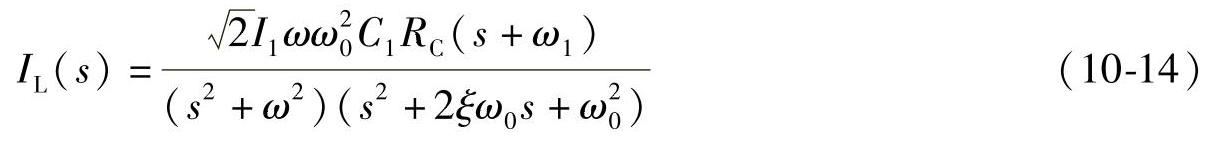
对其进行拉氏反变换，可以得到iL（t）的时域表达式为
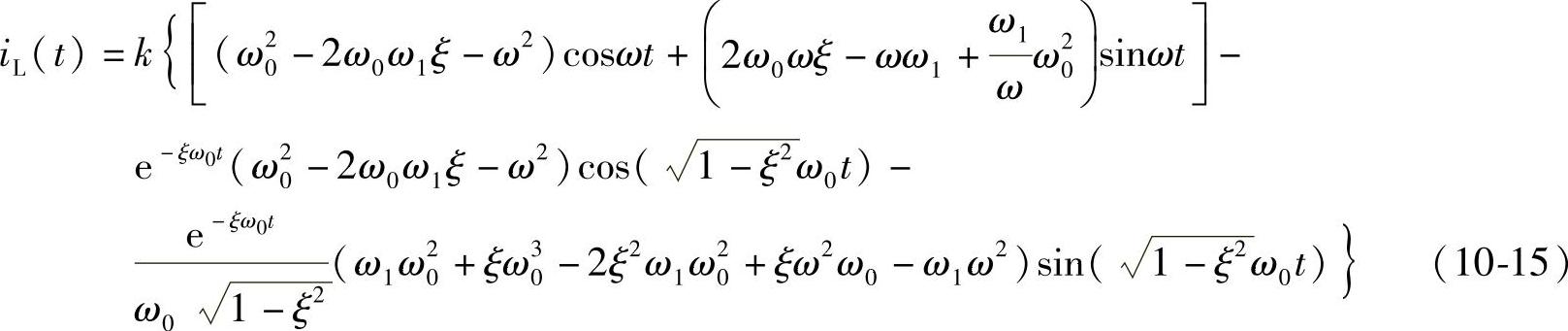
式（10-15）中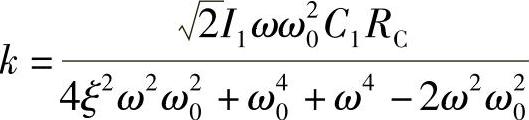
。从中可以看出，正弦电流激励产生的电流响应有两个分量：一个是强迫分量（式10-15中的第一项），它在LC低通滤波器作用下幅值有很大程度的衰减，衰减程度与滤波器参数以及正弦电流激励的频率等因素有关；另一个分量是暂态分量，它根据滤波器固有特性进行衰减，然而在暂态中仍会出现较大的振荡电流。
下面分别采用不同频率的电流对LC滤波器进行激励，逆变器直流侧电流id的峰值设为1000A，滤波电感L1=5mH，等效电阻RL=0.1Ω，滤波电容C1=8mF，等效电阻RC=0.1Ω。图10-10a是300Hz正弦激励id产生的iL电流响应波形，图10-10b是25Hz的id激励产生的iL电流响应波形。根据前面推导公式的计算结果，300Hz激励的电流响应约为12A，25Hz（接近谐振频率ω0）激励的电流响应约为4×1000=4000A，计算结果与仿真结果非常吻合。
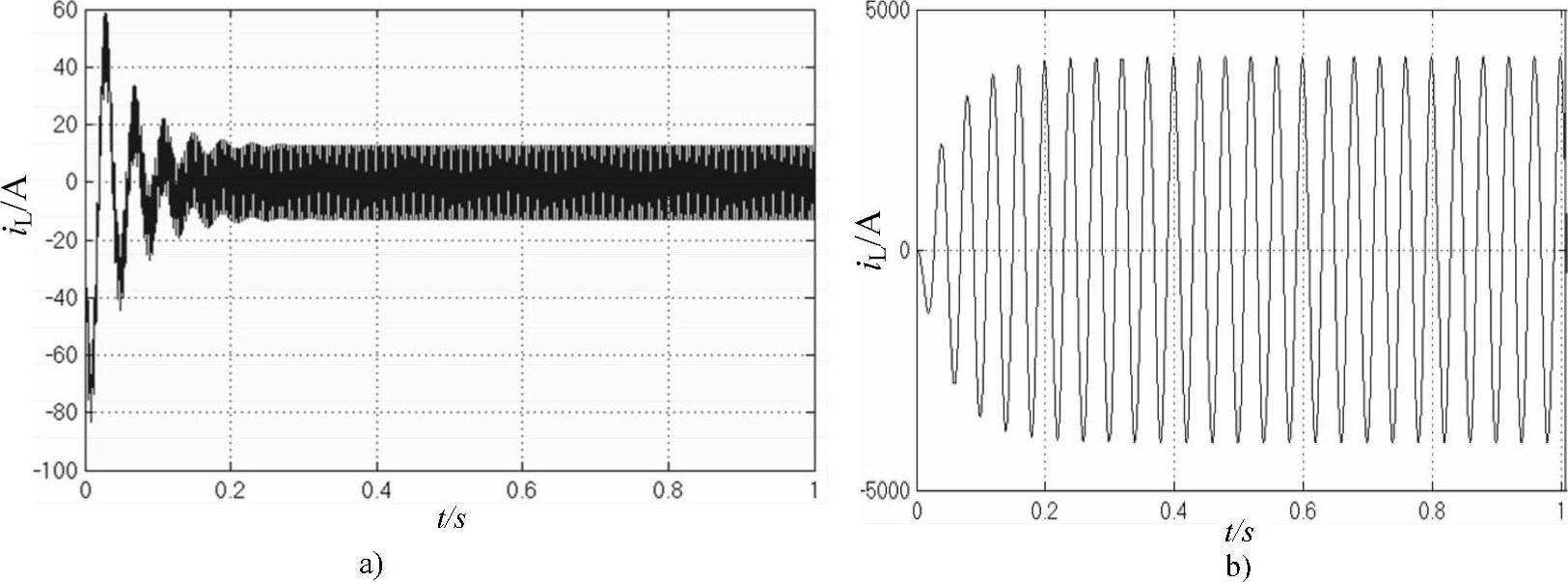
图10-10 iL电流仿真波形
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
