深入探讨SVPWM的几何特征

下面首先分析由图9-25所示的U₄、U₆两个电压矢量可以合成的电压矢量u_g的范围。换句话说，下面的分析是为了尝试分析适合采用U₄与U₆进行合成的期望电压矢量的空间位置特点。为不失一般性（多电平电压型逆变器中电压矢量幅值不相同），设

∣U₆∣=k∣U₄∣=kλ （9-12）

k为一个已知的正的常数，且它们之间的夹角为δ（满足0°＜δ＜180°），如图9-25b所示，根据图中的三角关系可以推导出下式：

由于余切函数在该区间是减函数，故0≤θ≤δ＜180°。这意味着，采用两个电压矢量按上述方法合成u_g总是位于两矢量的夹角范围内。

下面对采用两个电压矢量合成u_g的幅值特性进行推导与分析。设θ是一个定值，由式9-12知道q=t₂/t₁是一个定值。因为t₁+t₂≤t_g，所以有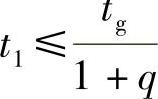。(www.xing528.com)

由三角形余弦定理可以得到

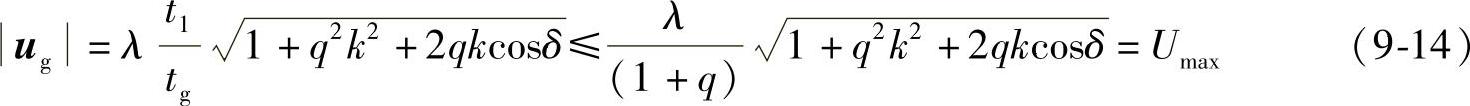
式9-14中，∣u_g∣的最大值U_max恰好就是图9-25b中线段OC的长度。这即是说，由U₄和U₆可以合成的幅值最大电压矢量的端点恰好就在线段AB上。

综上可知，从几何特征上说，采用两个电压矢量所能合成的等效电压矢量正好在由它们围成的三角形的内部与边界上（图9-25b中的阴影部分）。此外，还有如下结论：若u_g的方向固定，那么q=t₂/t₁就是一个定值，此时，两个非零电压矢量作用的总时间与期望合成的电压矢量的幅值成正比。当期望合成的电压矢量达到最大时，t₁+t₂=t_g也为最大。