PMSM运行稳定性分析优化

1.小信号模型推导

假定电动机已经运行在同步速度，那么在电动机受到一个微小的扰动，使其转子位置发生了变化时，对于前述的正弦交流电压供电的PMSM是否能够重新进入稳态运行？这是有关电动机运行稳定性的一个问题，下面采用传统的根轨迹方法进行分析。

为了分析电动机在工作点的稳定性问题，首先需要推导电动机在工作点的小信号模型。在转子dq坐标系中，PMSM的数学模型可以用式7-7～7-11表示（以隐极式电动机为例）。

u_d=U_1mcosγ

u_q=U_1msinγ （7-7）

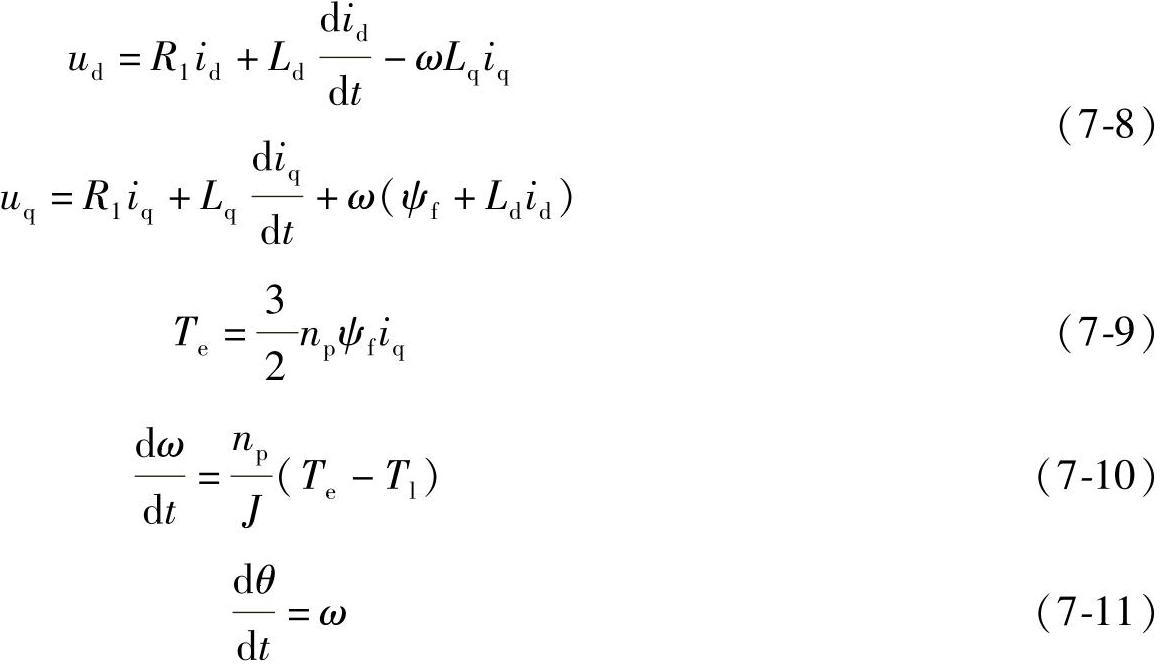
对于稳态的工作点，式7-8电压方程中的微分项为0，因此可以简化为式7-12。下标加0表示变量的稳态值

对于理想正弦交流电压源供电的PMSM来说，电动机稳态工作点的各个物理量在下角标中加入0作为标记，如式7-12和式7-13、式7-14。

u_d0=U_1mcosγ₀

u_q0=U_1msinγ0 （7-13）

当受到某种扰动，电动机转子的位置在很短的时间内突然产生了一个小的增量Δθ后，受其影响，多个变量产生增量，并且电压稳态方程7-12不再成立，需要改用动态方程式7-8。由于供电电源的频率未有改变，在转子dq坐标系中的电压矢量相位角发生变化，由于增量较小，近似有下式成立。

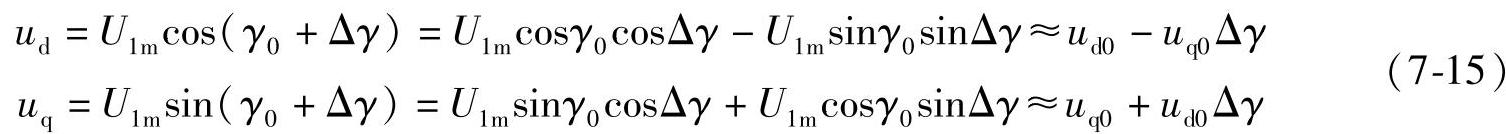
进而，可以求得dq轴电压的增量为

需要注意的是，式中的电压相位角是定子电压矢量相对于d轴的夹角，因而存在下式。

Δγ=-Δθ （7-17）

这里将动态电压方程式改写为下式（注意L_d=L_q=L）：

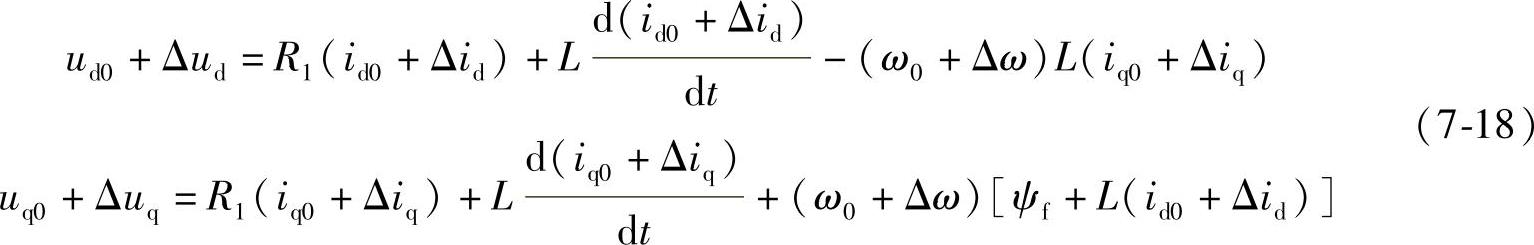
对式7-18进行分析，忽略其中的增量乘积，可以得到下式的增量方程式为

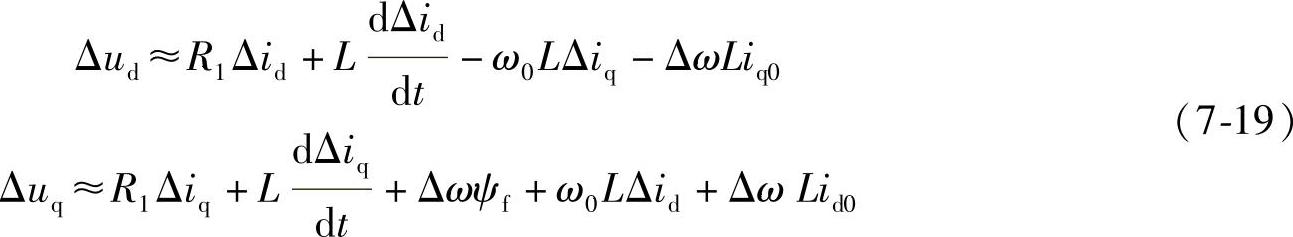
将式7-19进行拉普拉斯变换，改写为频域表达式，并且采用矩阵描述，得到

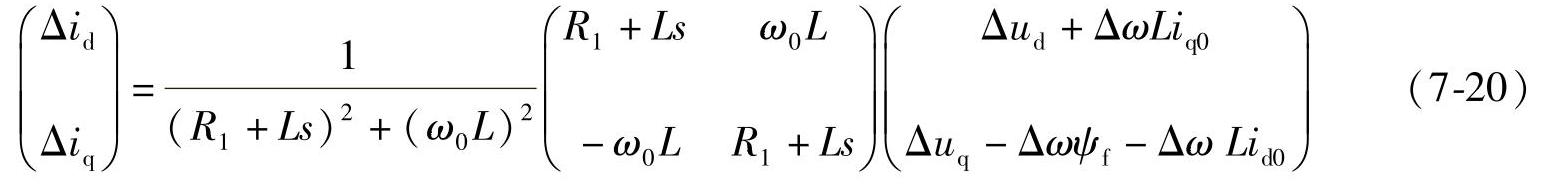
从7-20中可以计算出q轴电流的增量。根据式7-14，转矩的增量可以表示为

上面各方程式构成了PMSM速度增量系统，绘制成图7-10框图。

利用上述公式进行推导，可以得出图7-11中变形后的PMSM速度增量系统框图。

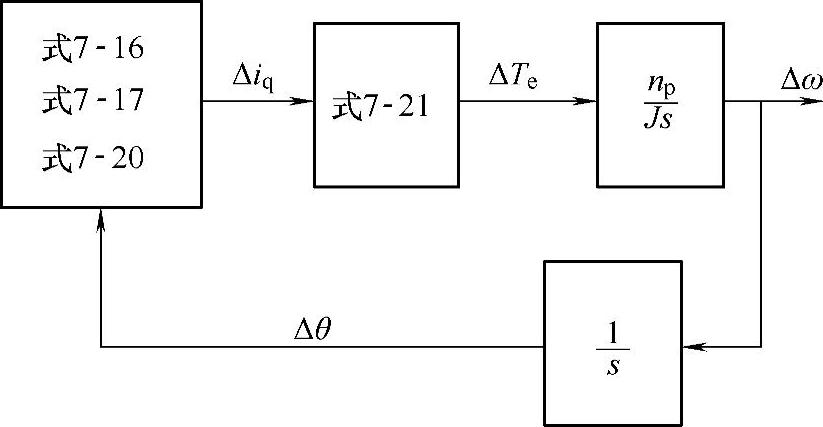
图7-10 PMSM速度增量系统的框图

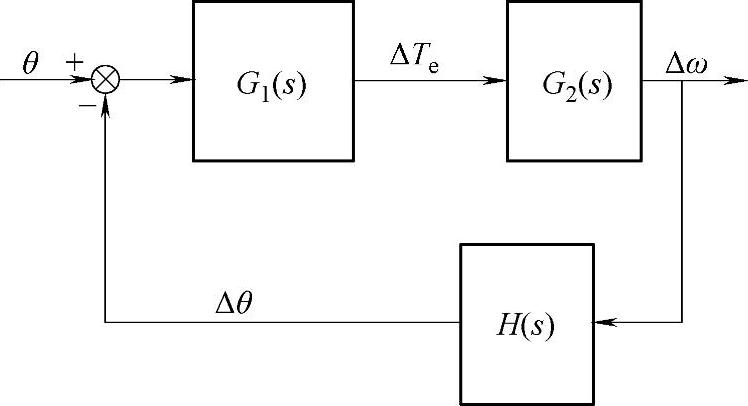
图7-11 变形后的PMSM速度增量系统框图

2.系统传递函数分析

图7-11中的各环节传递函数分别为

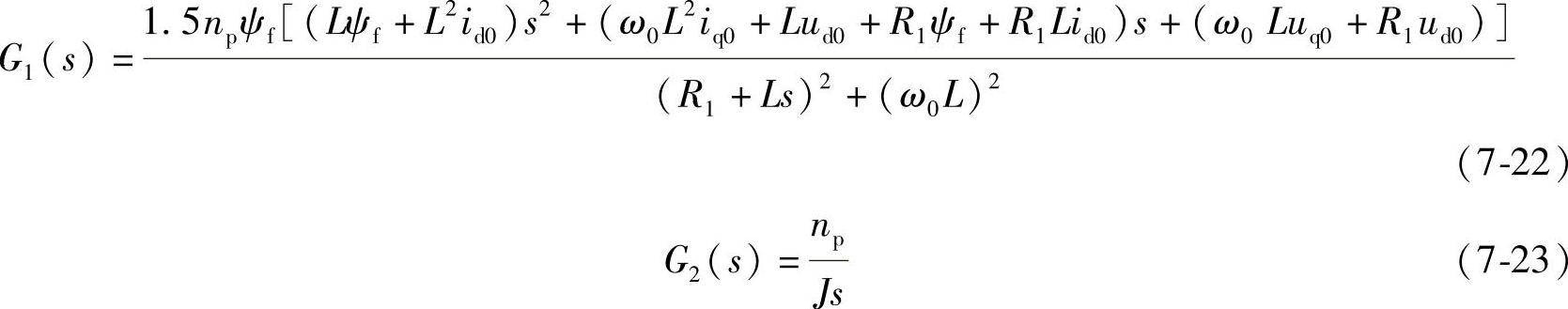
针对上述电动机系统，可以求出电动机转速增量Δω对位置增量Δθ的闭环传递函数。

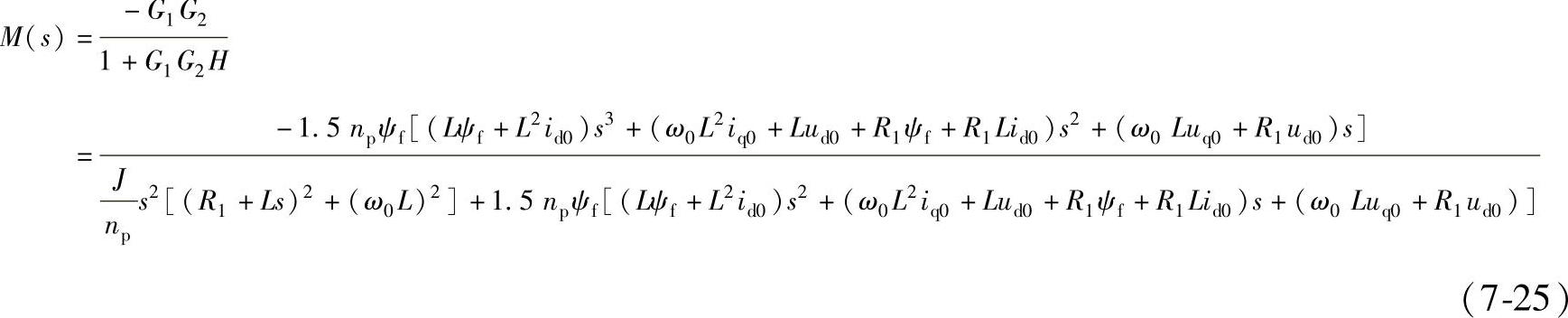
采用MATLAB程序进行分析为

经过上述的初始化以后，可以建立如图7-12所示的传函模型进行仿真分析。图中的step模块用于设置电动机转子位置角的扰动量，这里在0.001s的时候加入0.01弧度的扰动。

前面的仿真已经表明，不同机械惯量同步电动机的恒压恒频电压源供电下的起动过程有很大区别。这同样也适用于电动机工作的稳定性分析。对于图7-12中的仿真模型，设置不同的转动惯量，可以发现电动机工作点的稳定性有很大差异。

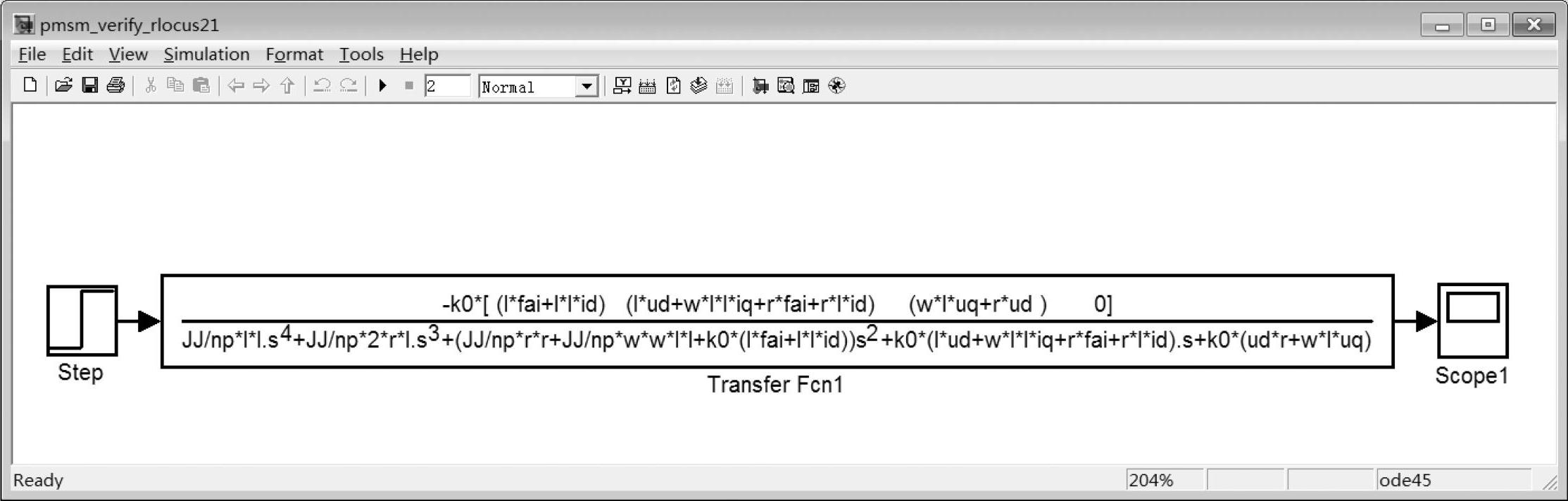
图7-12 检验电动机工作点稳定性的仿真模型

图7-13给出的是电动机转动惯量为1.2时，电动机转子位置受到扰动后的转速波形，发现短时间内电动机的转速呈现近似等幅振荡，这表明电动机的阻尼非常小，近似为0，电动机的稳定性较差。通过对传递函数的极点——特征方程的根进行分析，可以得到当电动机转动惯量约为2.315e-4时，电动机处于临界阻尼（即阻尼为0）。小于该转动惯量，电动机的阻尼为正；大于该转动惯量，电动机的阻尼为负，系统将会不稳定。

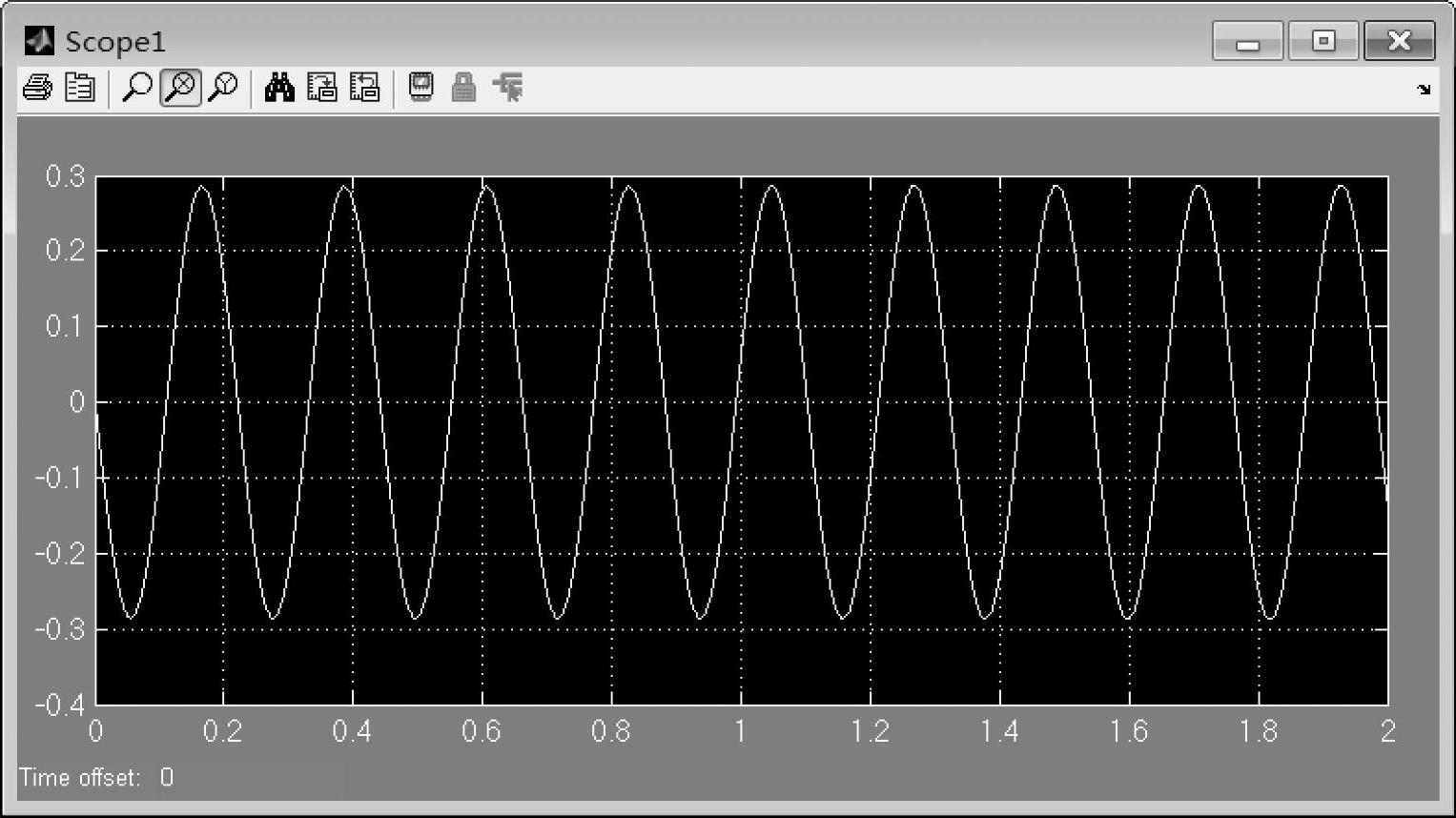
图7-13 转动惯量为1.2时的转速增量波形

当转动惯量为1.2e-2时，图7-12仿真的结果如图7-14所示，可以看出，系统呈现较为明显的发散现象。其中转速的波动周期略大于0.02s，这个数值与后面给出的转动惯量为1.2e-2时系统极点的振荡频率相吻合。

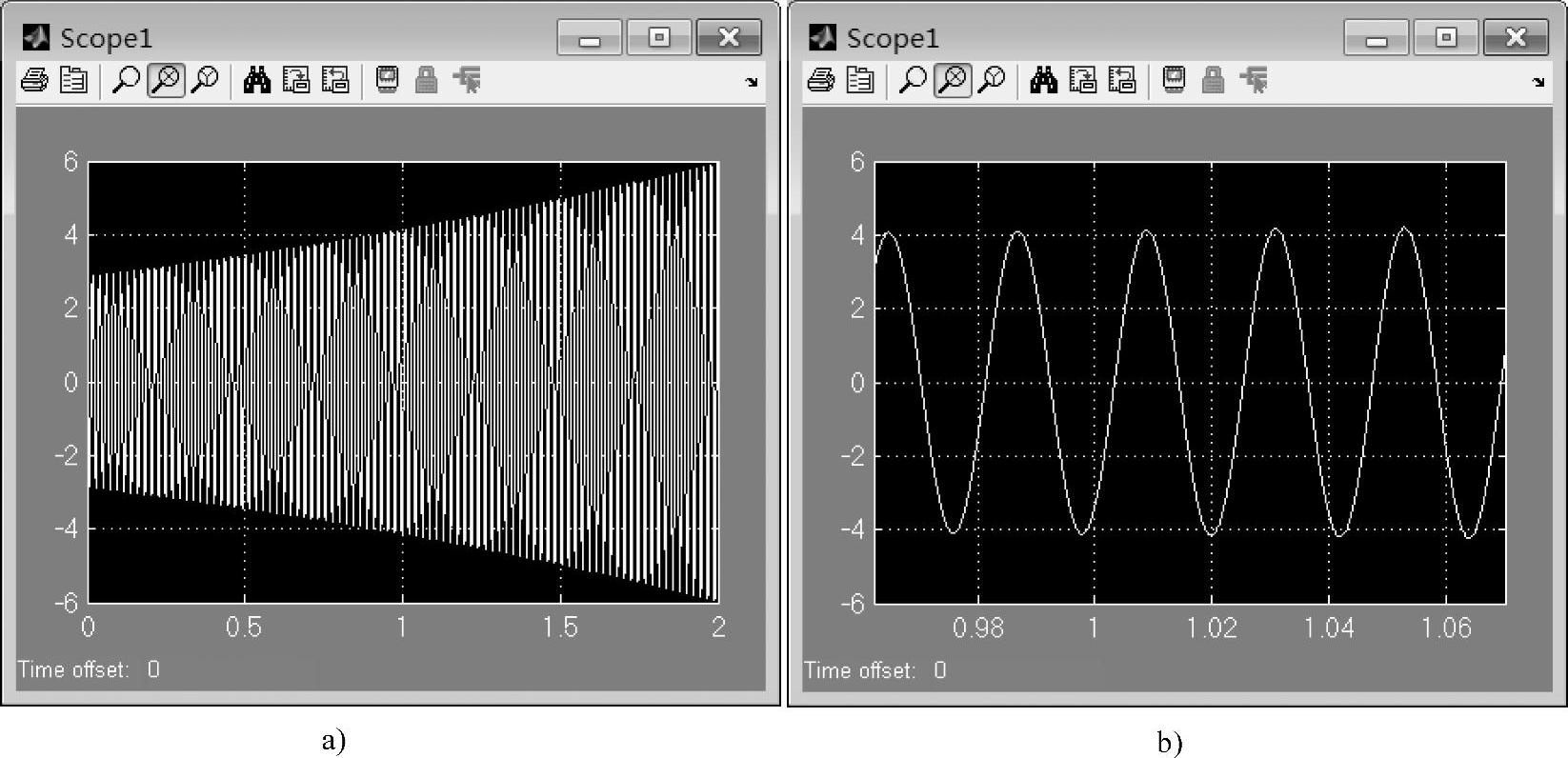
图7-14 转动惯量为1.2e-2时的转速增量仿真波形

图7-15给出了转动惯量为1.2e-1时的仿真波形图，转速同样也在发散，并且其振荡周期接近0.07s。

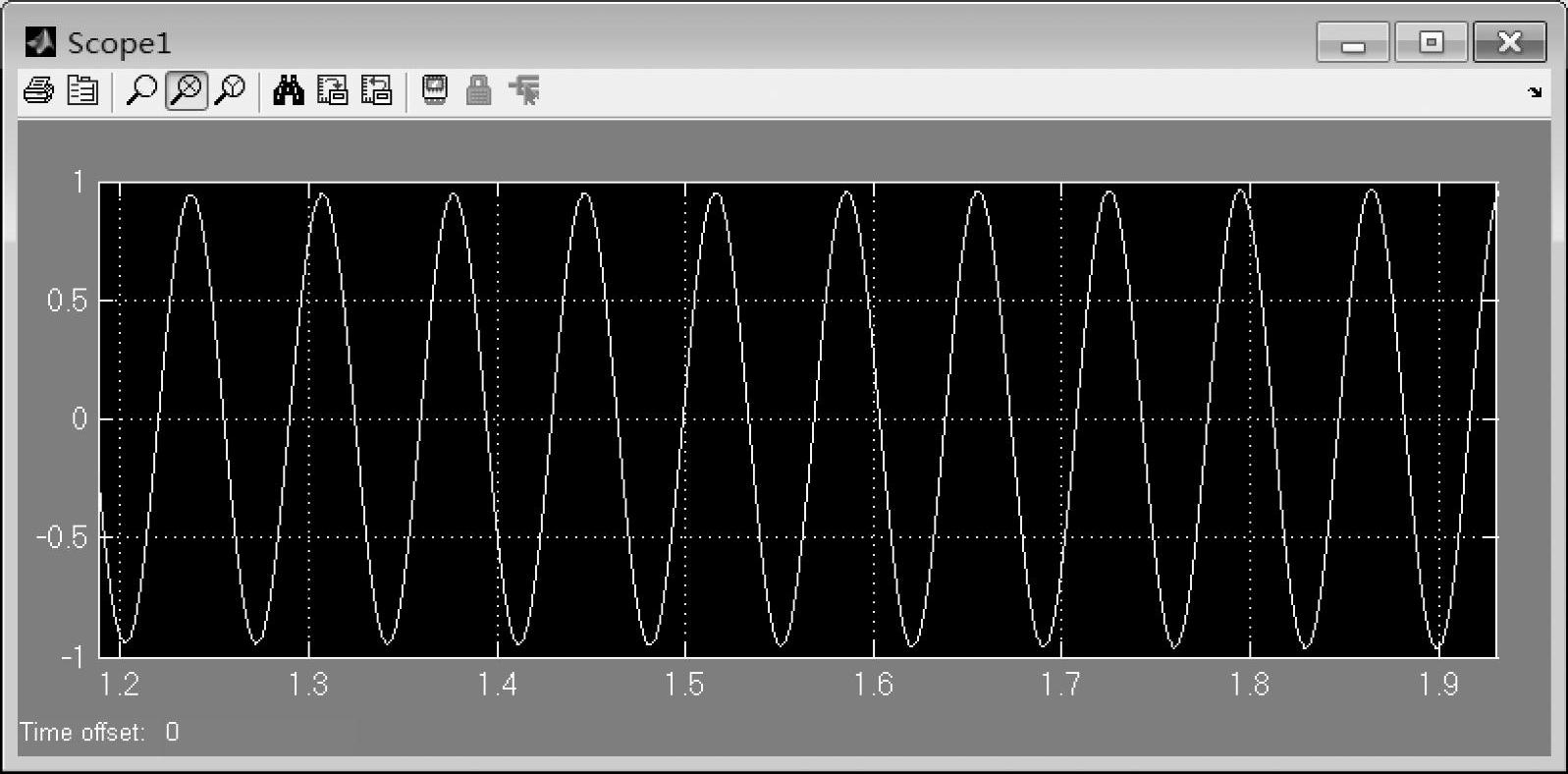
图7-15 转动惯量为1.2e-1时的转速增量仿真波形（放大后）

当已知电动机的转动惯量，计算特征方程的根可以利用下面的MATLAB程序。

首先，利用MATLAB命令solve（＇a*s^4+b*s^3+c*s^2+d*s+f=0＇，＇s＇）求出通解。由于是4阶方程，所以会有4个解，符号变量表示的通解异常复杂，这里不再给出。

在设置如下变量（a、b、c、d、f）后，利用MATLAB得到的通解就可以求解出具体的4个解。

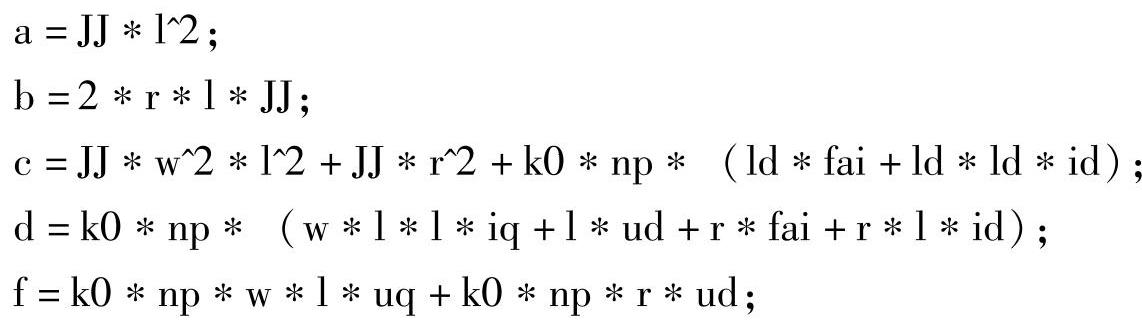
当转动惯量为1.2e-4时的4个解为：

当转动惯量为2.315e-4时的4个解为：

当转动惯量为1.2e-3时的4个解为：

当转动惯量为1.2e-2时的4个解为：

当转动惯量为1.2e-1时的4个解为：(https://www.xing528.com)

当转动惯量为1.2时得到的4个解为：

从转动惯量为1.2e-2的特征根可以看出，不稳定的特征根的振荡角频率约为285rad/s，对应的振荡频率约为45Hz，其振荡周期约为0.022s，略大于0.02s，结果与图7-14的仿真结果相吻合。

3.根轨迹分析

下面采用MATLAB根轨迹工具对转动惯量J与闭环系统极点的关系进行分析。首先将闭环系统特征方程改写为下式：

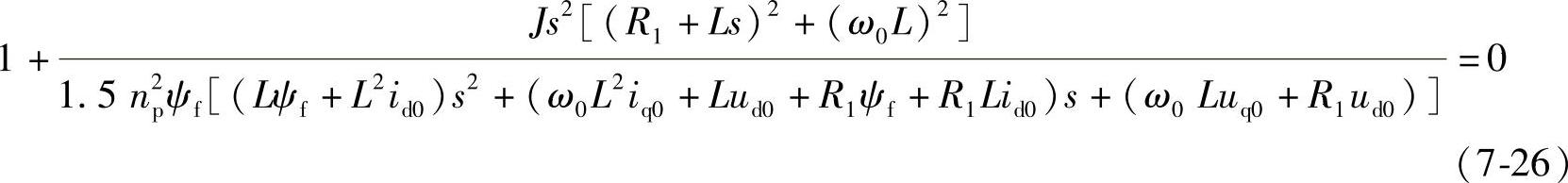
然后采用下述的MATLAB程序就可以针对变量J进行系统根轨迹的分析。

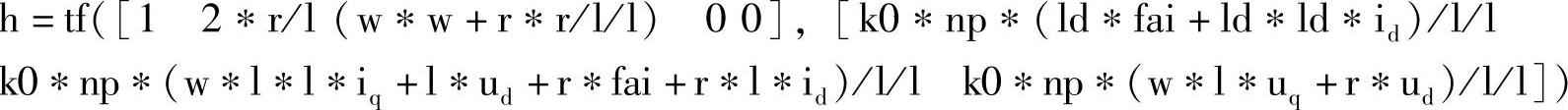
%设置待分析的传递函数

rlocus（h）%进行根轨迹分析

[rr，kk]=rlocus（h）%计算出增益kk（这里即是惯量J）与根rr（相应极点）。

采用上述程序得到的根轨迹如图7-16所示，放大后如图7-17所示。可以看出系统有两个有限的复数极点（在左半平面靠近虚轴处）和两个无穷远处的极点，系统有四个零点——两个同在原点处，另外两个复数零点在两个复数极点的左侧。当转动惯量分别为2.315e-4、1.2e-4、1.2e-3、1.2e-2、1.2e-1和1.2的时候，右下角根轨迹的对应点分别为A、B、C、D、E、F。可以看出，D、E、F几个点非常靠近原点，系统呈现近似等幅振荡的现象，前面图7-13正是对F点的仿真波形。

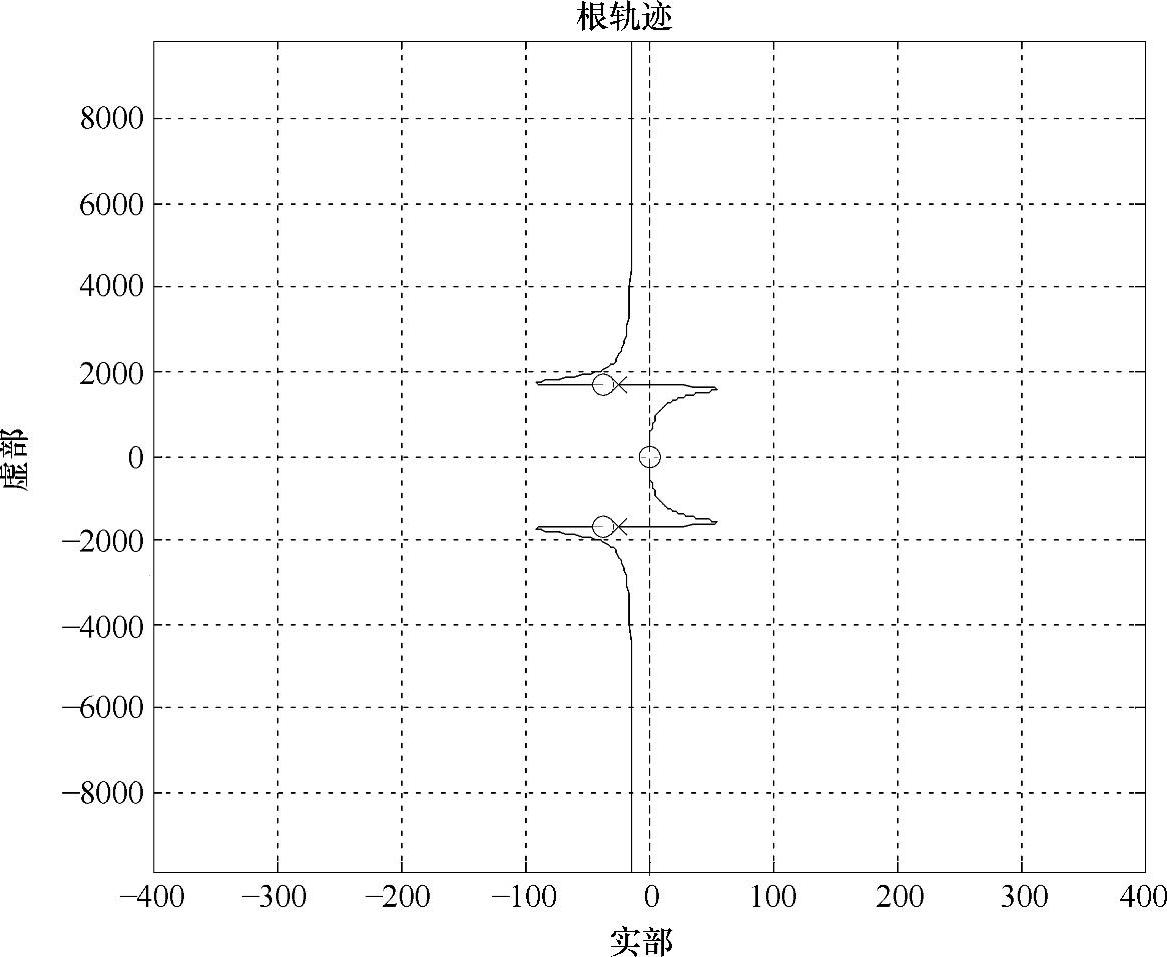
图7-16 关于转动惯量的系统根轨迹图

4.仿真验证

另外，为了进一步验证上述分析结果，针对第3章建立的电动机动态仿真模型（见4.2内容）进行SIMULINK动态仿真。首先根据前述命令计算出系统在不同输出转矩下的初始状态，包括电动机机械角转速（同步速度）、i_d、i_q、电压相位角的初始值以及转子位置角扰动量，然后分别在不同转动惯量下进行仿真。

空载下的各变量初始值分别为417.8rad/s、240A、0A、1.56rad，负载180Nm下的各变量初始值分别为417.8rad/s、-12.5A、545.5A、2.4rad。100Nm负载转矩下的初始值为417.8rad/s、170A、303A、1.987rad。

图7-18给出了空载下，设置初始值后未加扰动量的仿真波形。很容易看出，系统直接进入稳态运行，这就避免了仿真中因为初始值的设置偏差造成暂态振荡的发生。

图7-19给出了转动惯量为1.2时的转速波形图，仿真200s后，可以看出它呈现出极其微小的发散状态，这也表明系统极点位于右半平面非常靠近虚轴的地方。

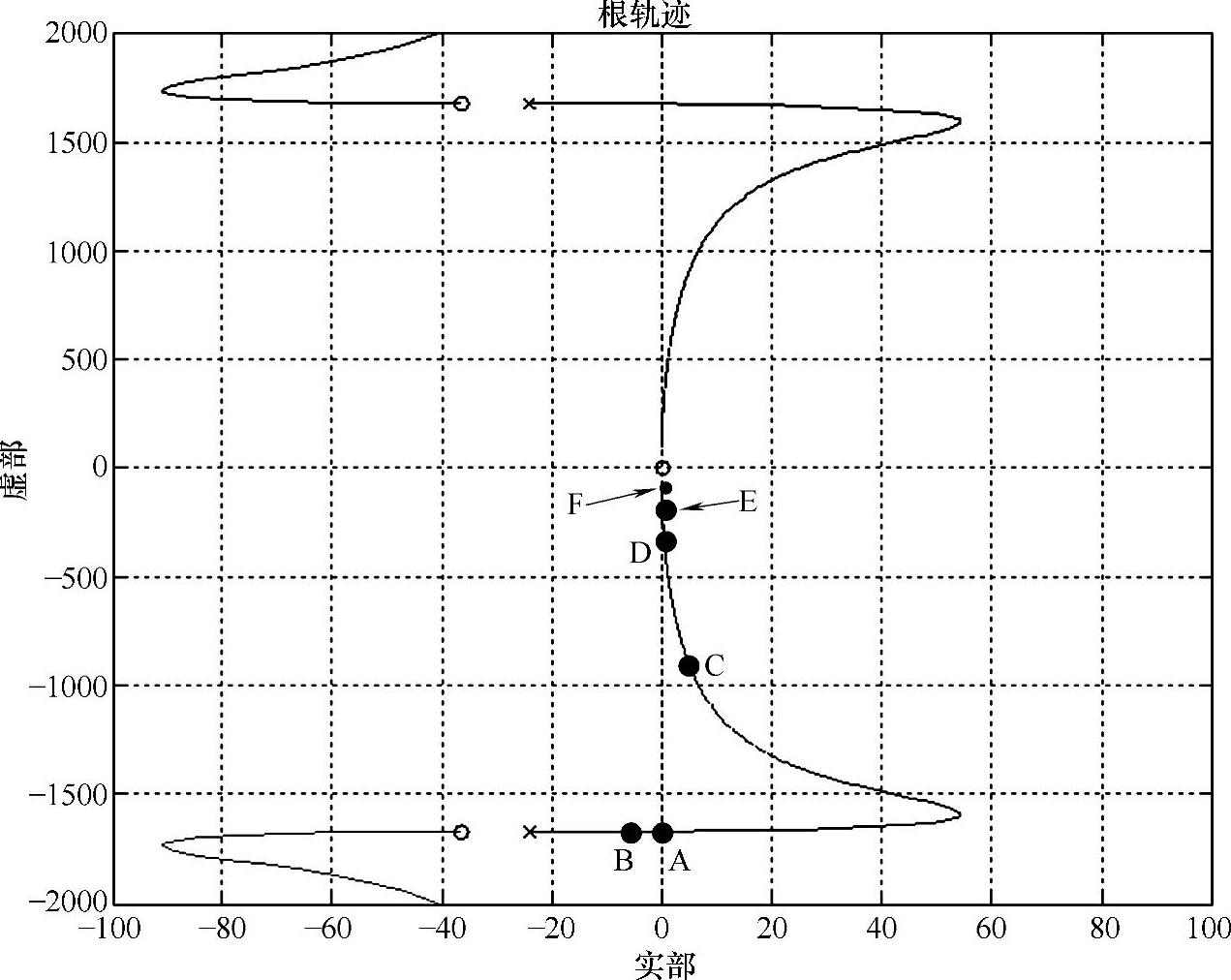
图7-17 根轨迹放大图

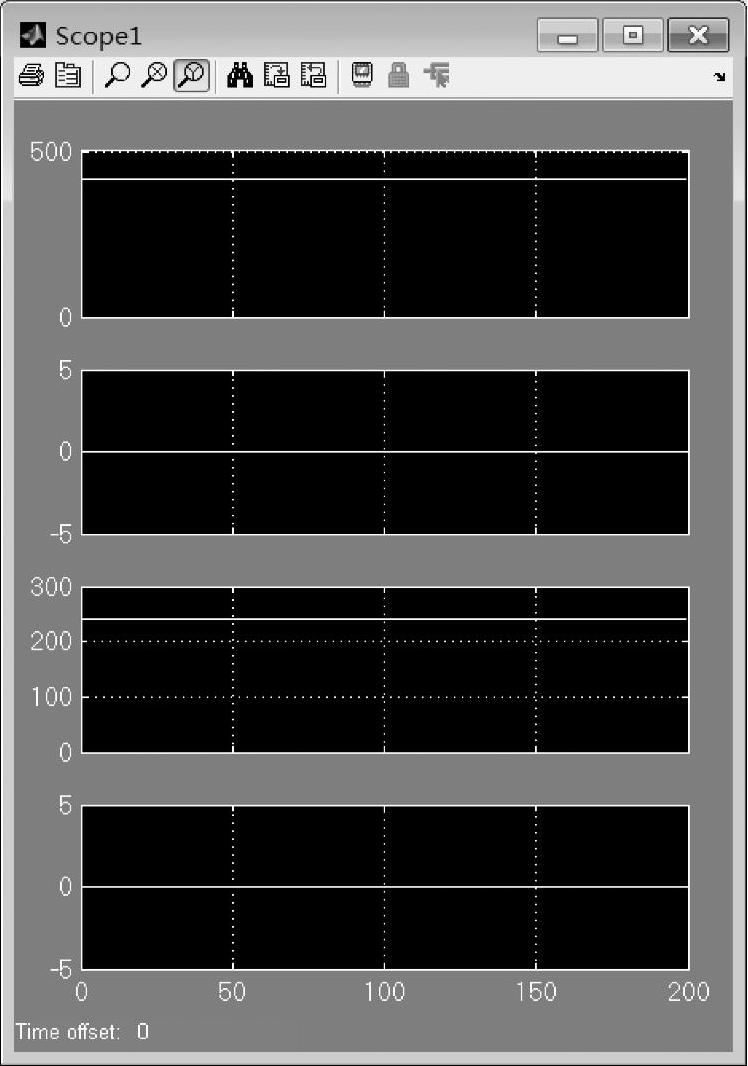
图7-18 正确设置初始值后无扰动时的仿真波形图

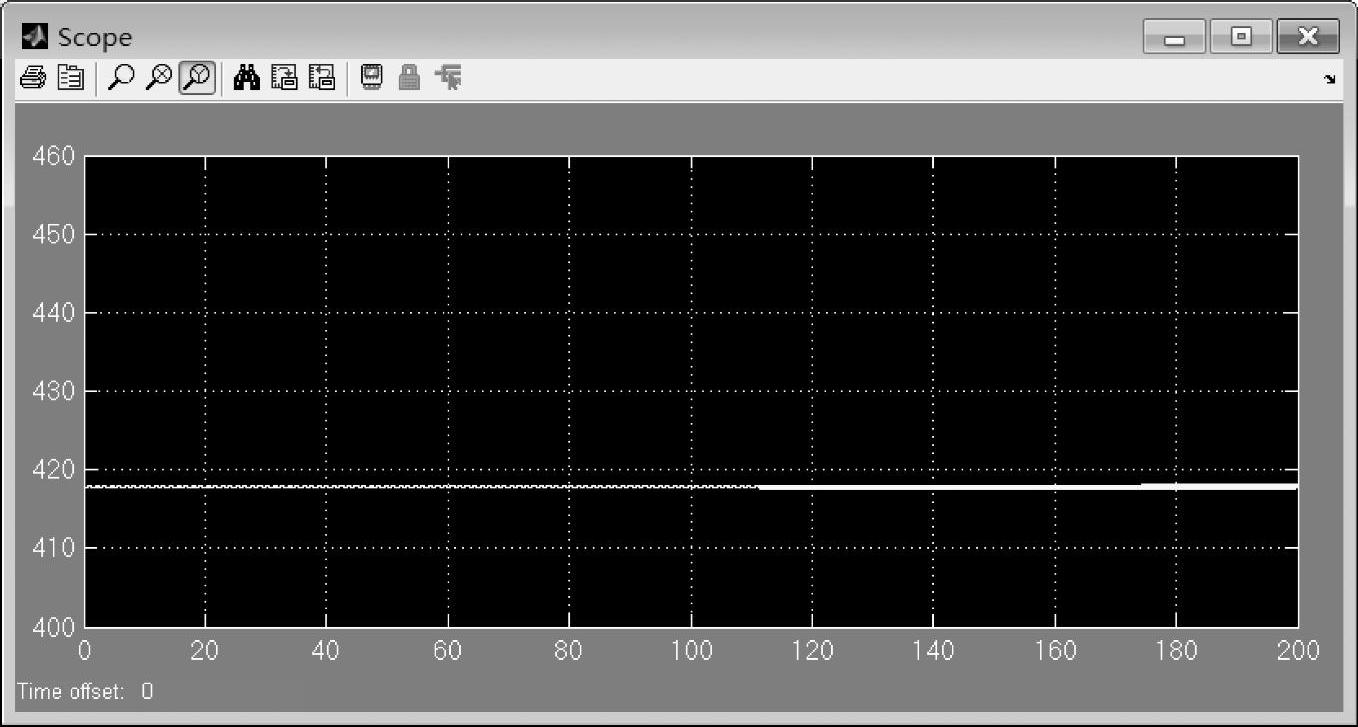
图7-19 转动惯量为1.2时的转速波形图

图7-20给出了转动惯量为1.2e-1时的转速波形图，仿真到120s后，可以看出它呈现出较为明显的发散状态。这说明转动惯量的减小，系统极点远离了虚轴。

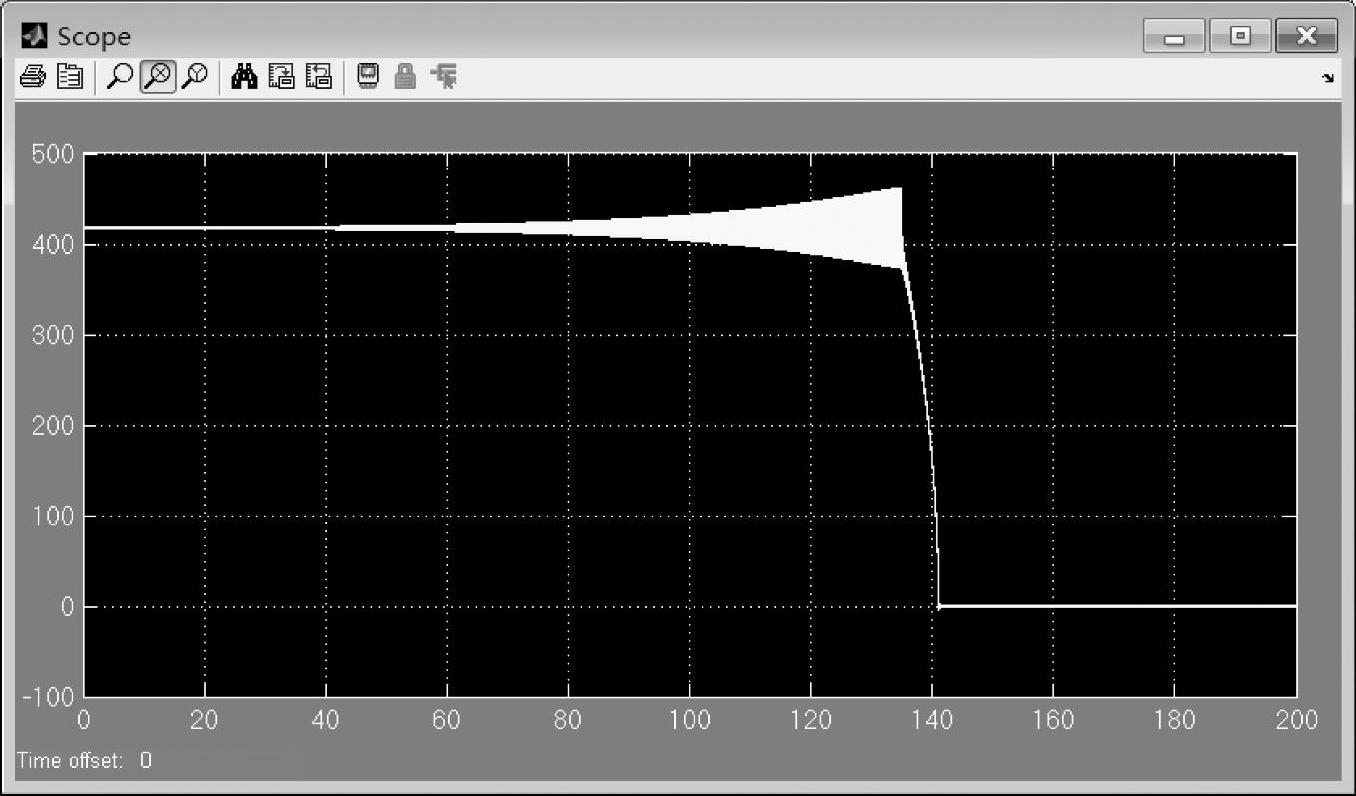
图7-20 空载下转动惯量为1.2e-1时的转速波形图

图7-21将图7-20的波形在14s附近进行放大，可以从局部看出，系统似乎处于等幅振荡中。另外，可以估算出振荡周期大约为0.07s，这与图7-15以及根轨迹计算的系统右半平面极点的虚部都是相吻合的。

图7-22给出了图7-20在120s附近的放大波形图，此时可以估算出转速波形的振荡周期约为0.08s，与前面的分析出现了偏离，这是因为此时转速偏离前面的稳态工作点已经较大，所以前面的计算公式就会出现较大偏差。

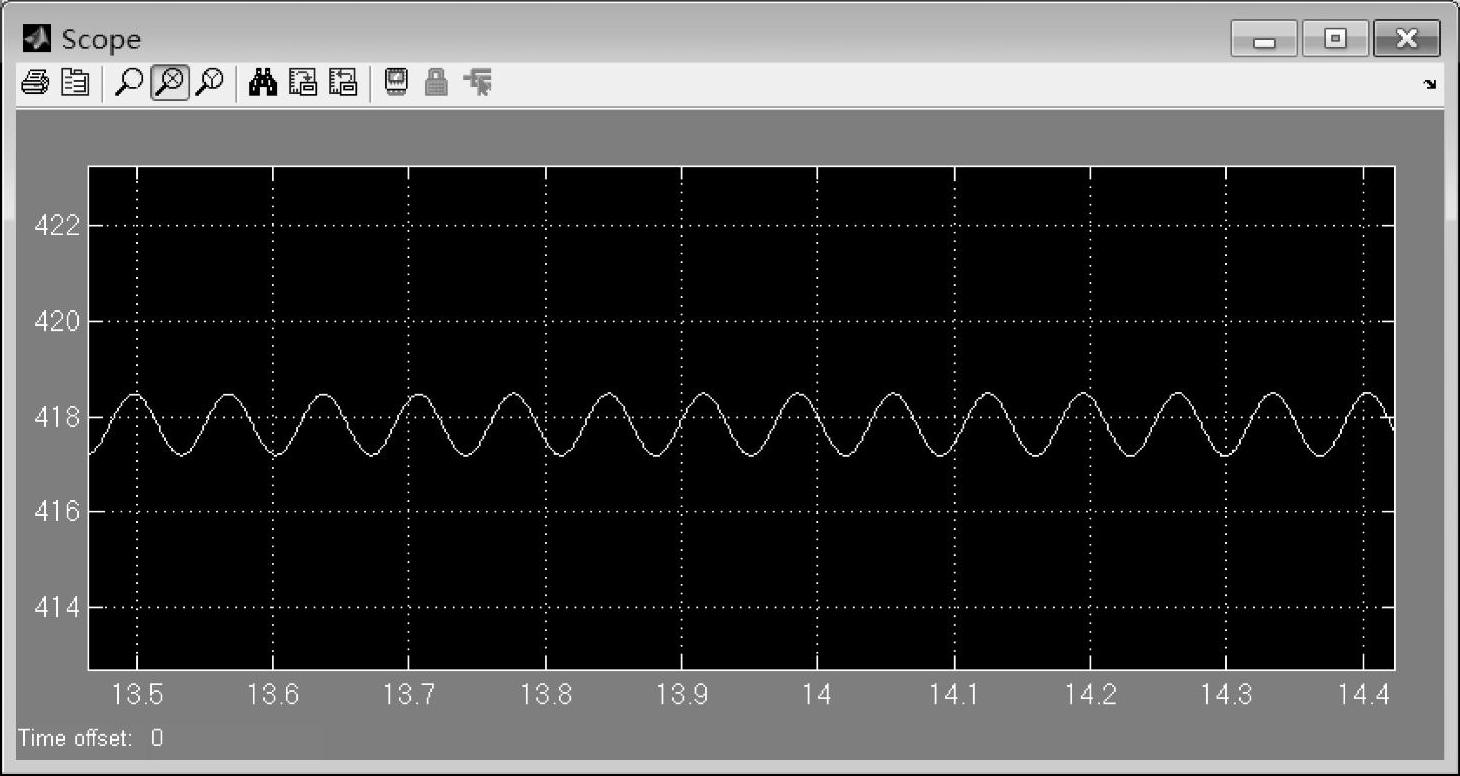
图7-21 转动惯量为1.2e-1时的转速波形放大图（小幅度振荡时）

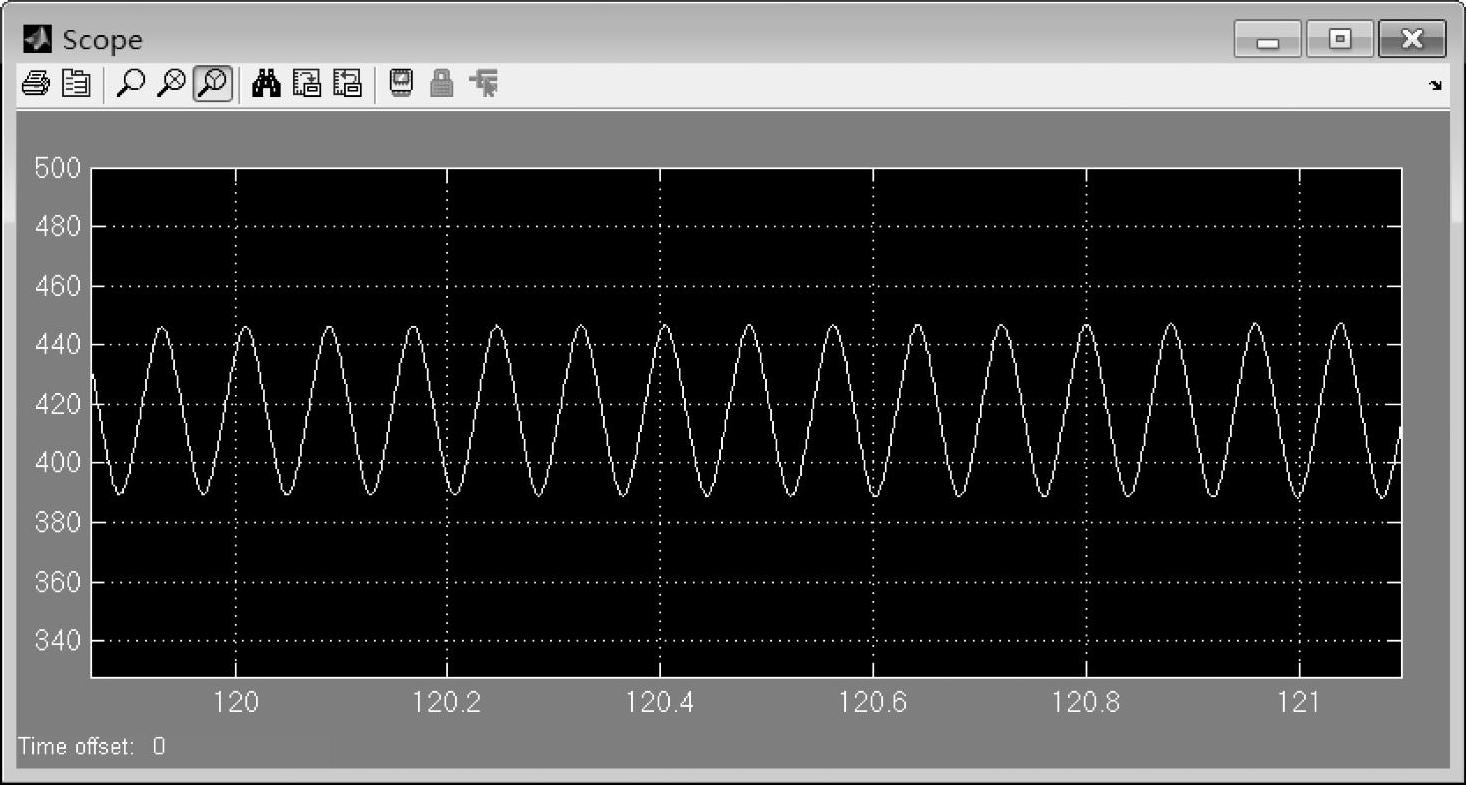
图7-22 转动惯量为1.2e-1时的转速波形放大图（大幅度振荡时）

图7-23给出了加入100Nm负载以后、转动惯量为1.2e-1时的转速波形图。由于电动机转矩的实际输出能力下降较快，其均值约为0，无法与负载平衡。所以在负载转矩的作用下，电动机转速迅速减少。

图7-24给出了转动惯量为1.2e-2时的转速波形图，图7-25给出了对应的电动机转矩波形图。可以看出转速的发散状态继续加强。由于电动机转矩的振荡，无法保证0转矩的输出，所以仿真到15s后，电动机速度开始下降。最后电动机的转矩围绕0上下波动，电动机的转速也就在0附近。

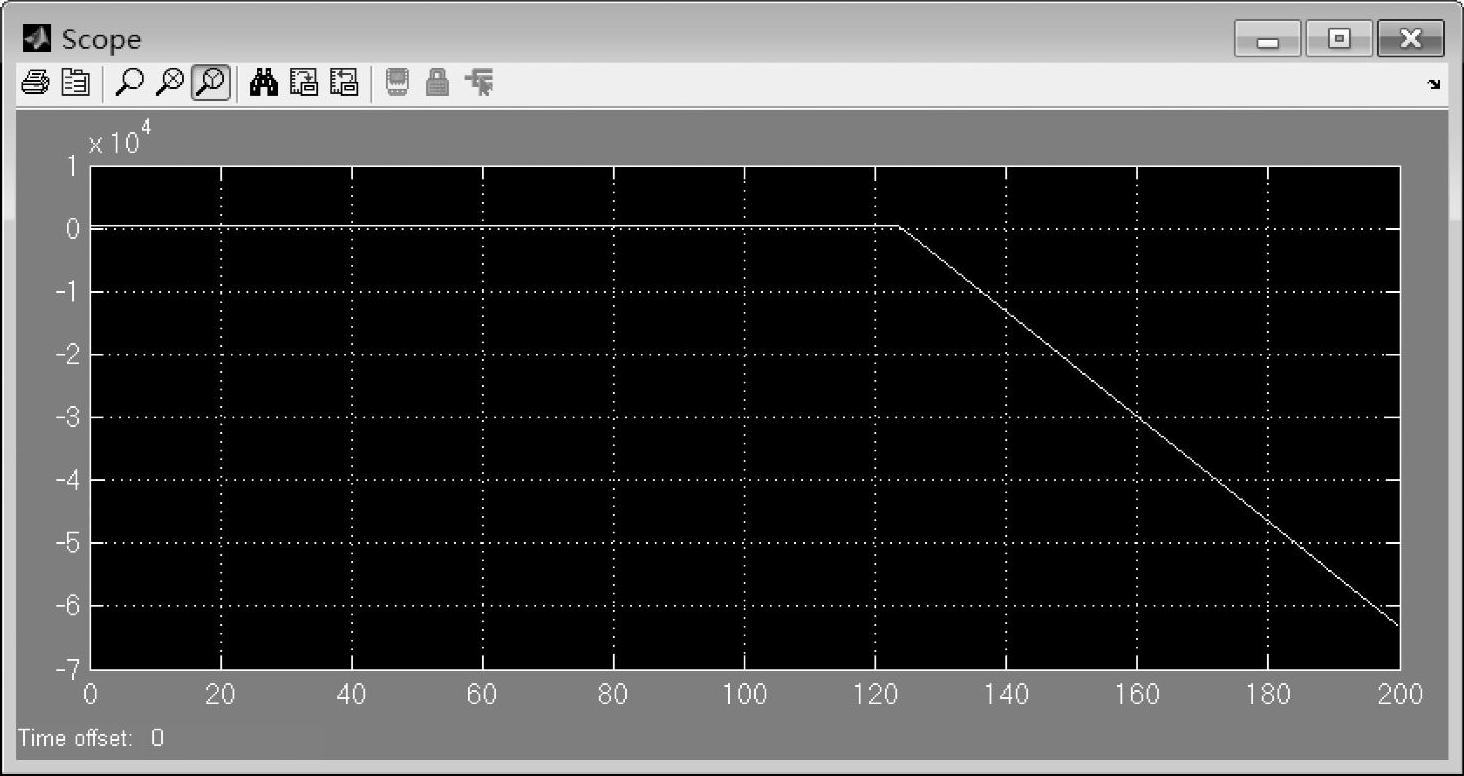
图7-23 负载100Nm下转动惯量为1.2e-1时的转速波形图

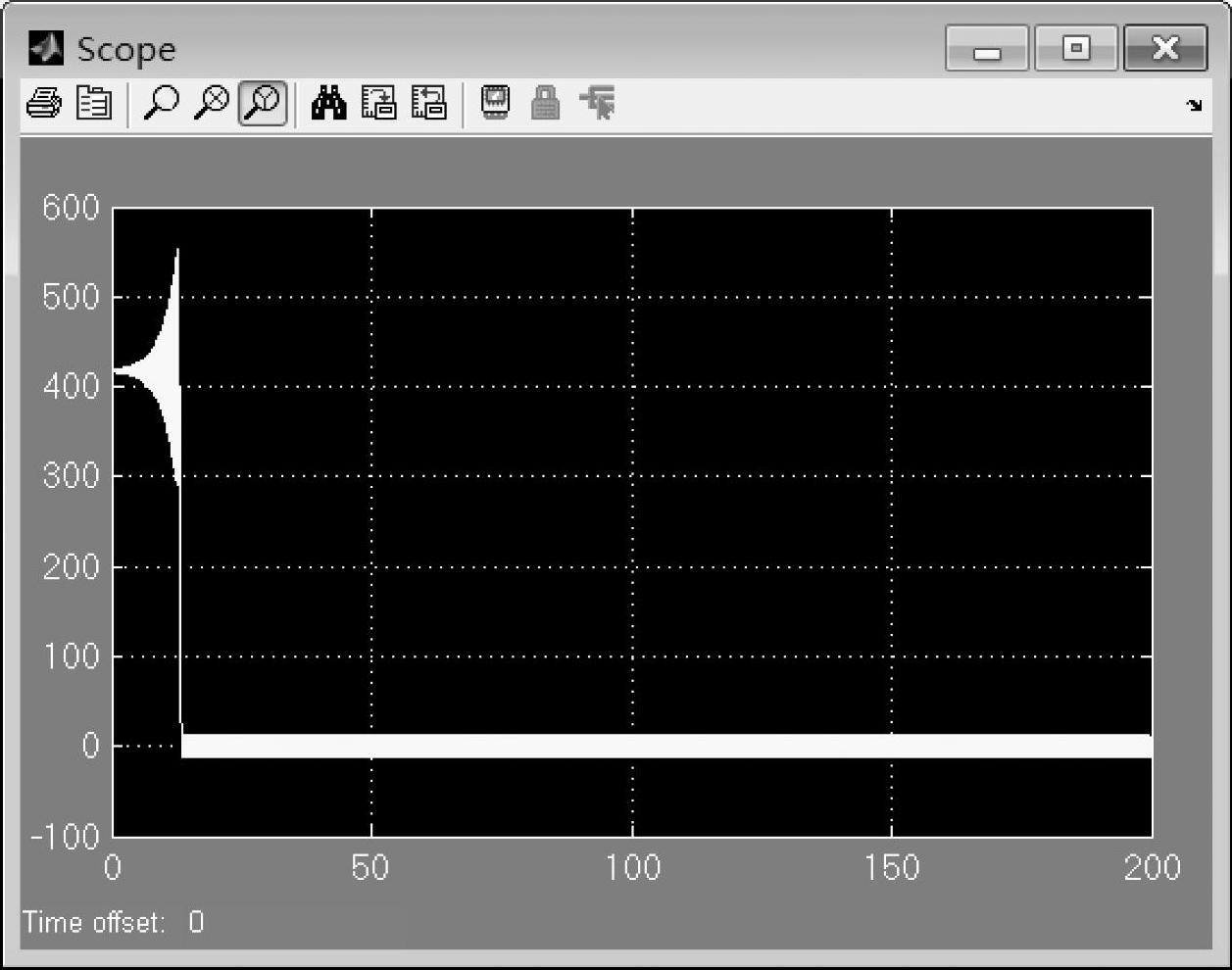
图7-24 空载下转动惯量为1.2e-2时的转速波形图

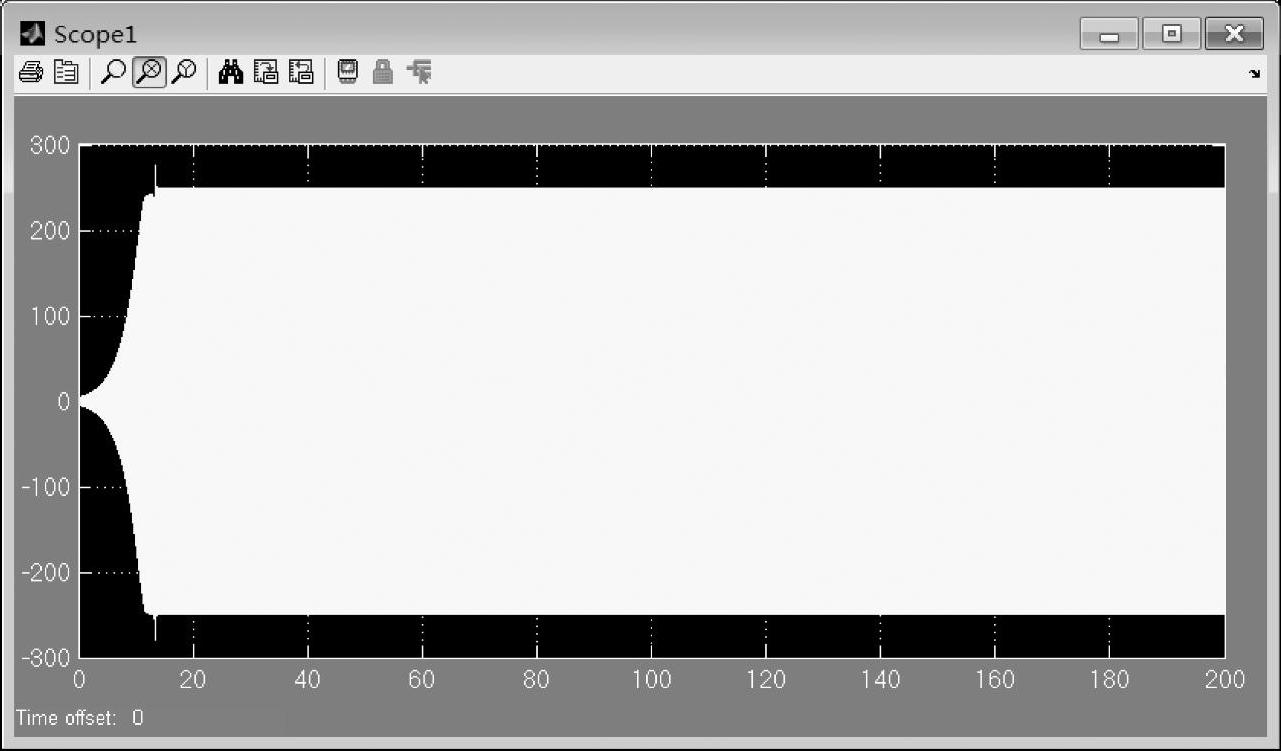
图7-25 空载下转动惯量为1.2e-2时的转矩波形图

图7-26给出了转动惯量为1.2e-4时的转速波形图，图7-27是加入负载100Nm的转速仿真波形。可以看出，加入扰动以后，电动机转速出现振荡，但随即开始明显衰减。这是由于系统的极点位于左半平面，并且距离虚轴较远——从前面计算的系统极点可以知道。

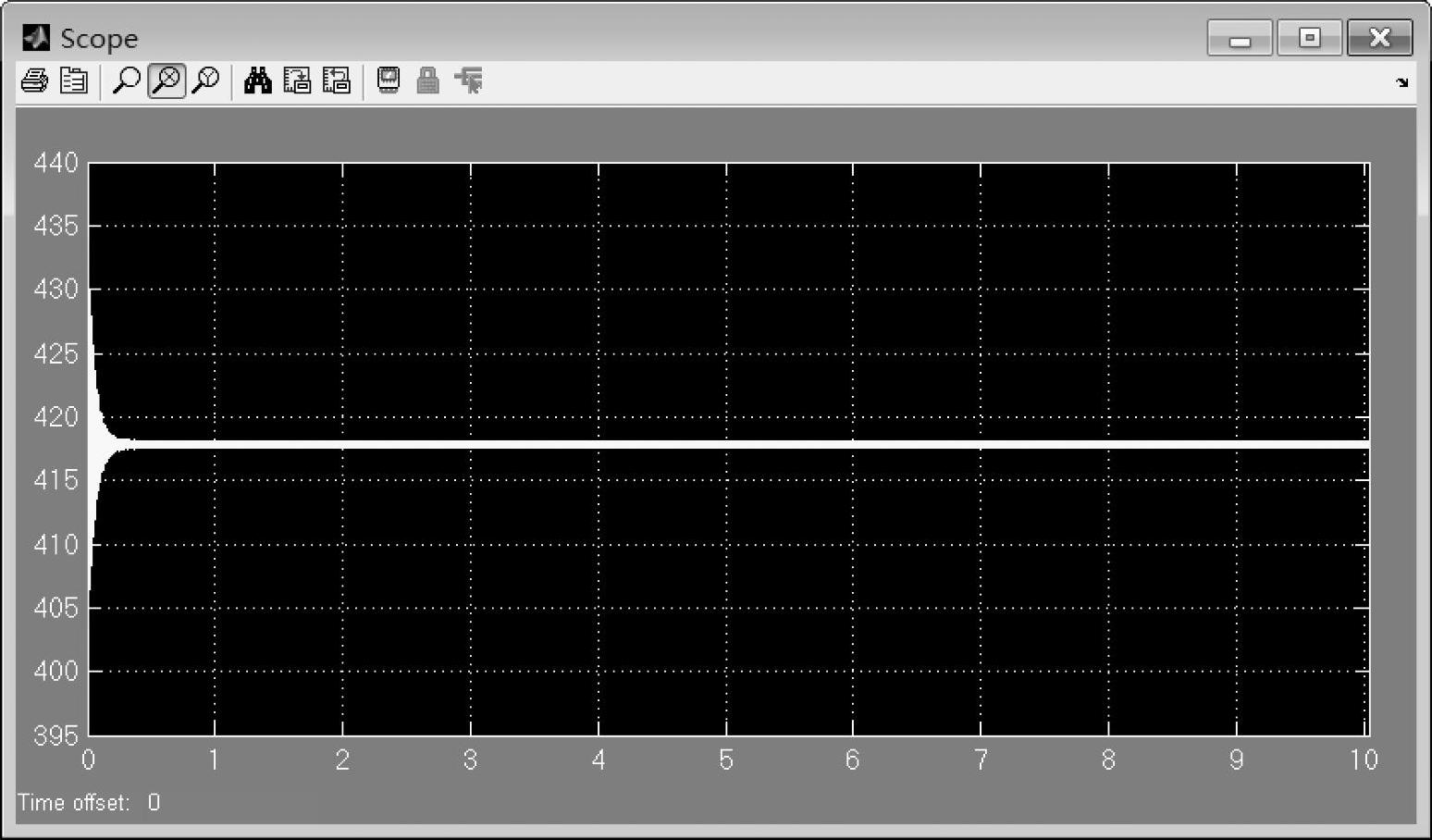
图7-26 空载下转动惯量为1.2e-4时的转速波形图

细心的读者可能会发现一个问题，系统进入稳态后为何转速以及转矩还是在振荡，怎么没有衰减了？这与仿真环境有关系。因为前面是需要仿真200s，时间较长，所以系统的最大步长设置为1e-3。为了弄清楚电动机最后是否还会有振荡存在，可以设置仿真最大步长为1e-5，重新仿真的结果如图7-28所示，仿真步长设置如图7-29所示。结果很明显地表明系统是稳定的。

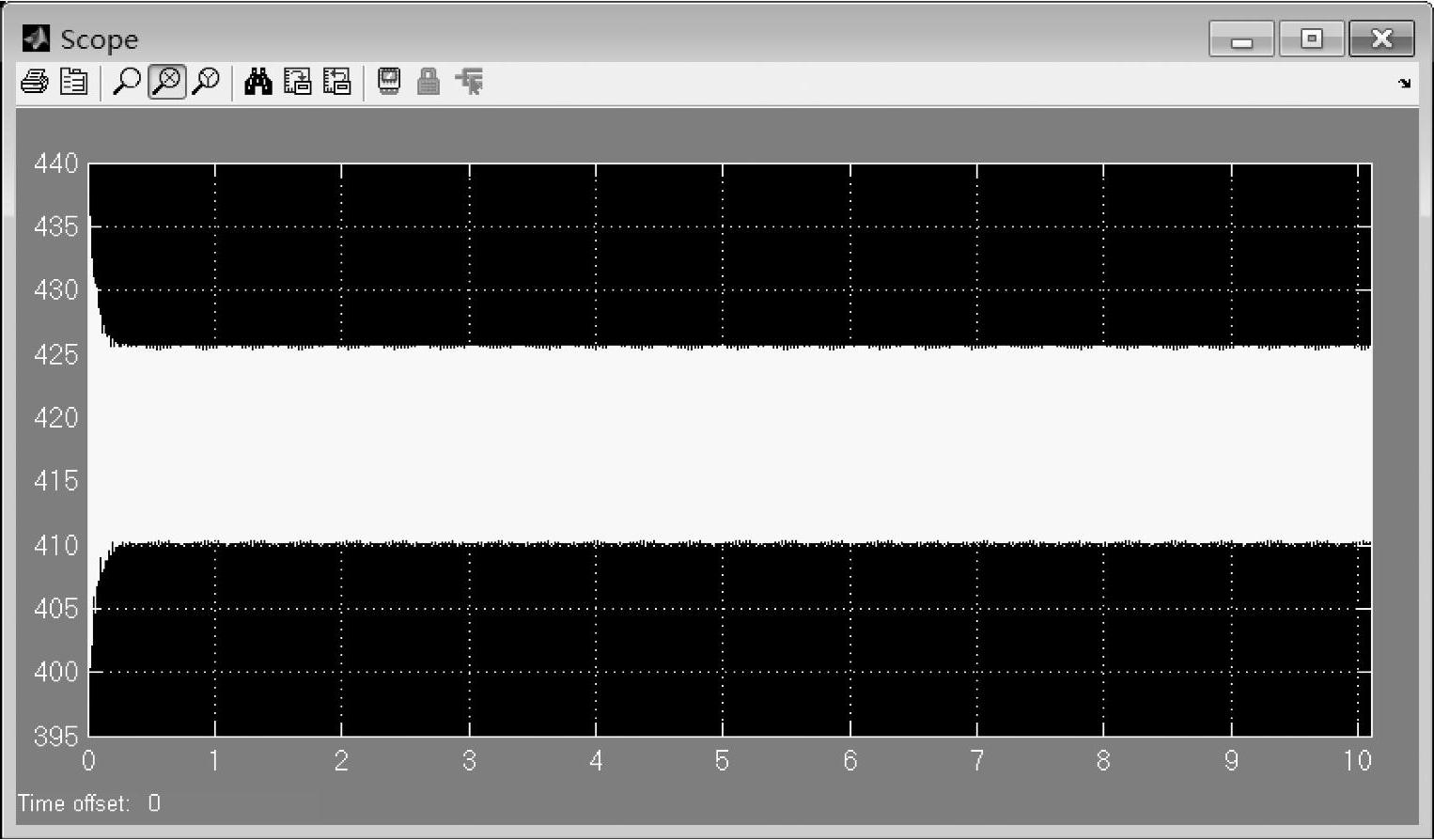
图7-27 100Nm负载下转动惯量为1.2e-4时的转速波形图

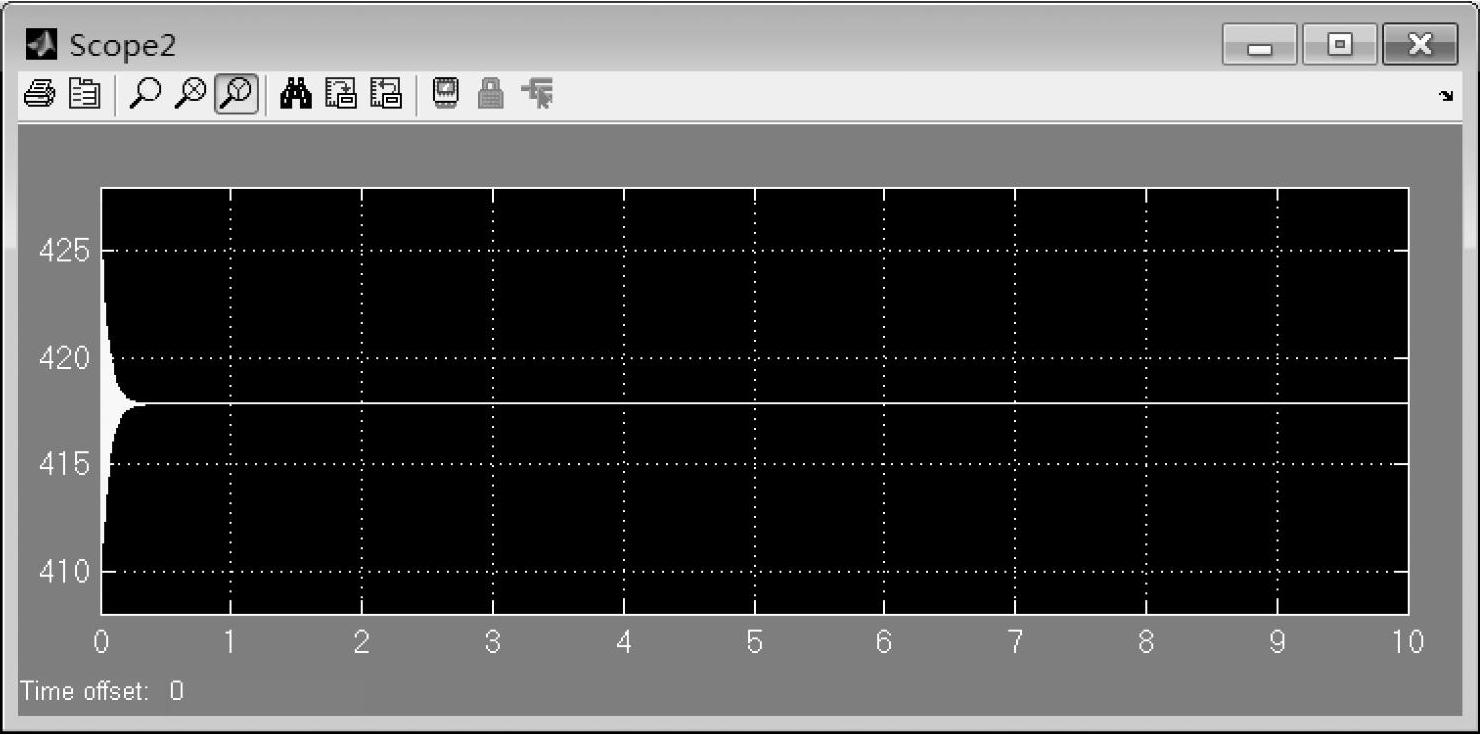
图7-28 空载下转动惯量为1.2e-4时的转速波形图（减小最大步长后的仿真）

这里再对转速波形的衰减过程进行定量的分析。根据前面提供的转动惯量为1.2e-4时的系统极点可以看到，此时系统的极点全部在左半平面，其中一对为（-18.7+j2852）和（-18.7-j2852），另一对为（-17.6+j1671）和（-17.6-j1671）。

放大仿真波形后，从中可以估算出，振荡开始时的最高转速约为427.2rad/s，在0.2s时的转速约为417.5rad/s，稳态转速为417.8rad/s。假定系统只有第一对极点，按照指数规律进行衰减，那么时间为t时的转速增量应为

Δω=ke^σt （7-27）

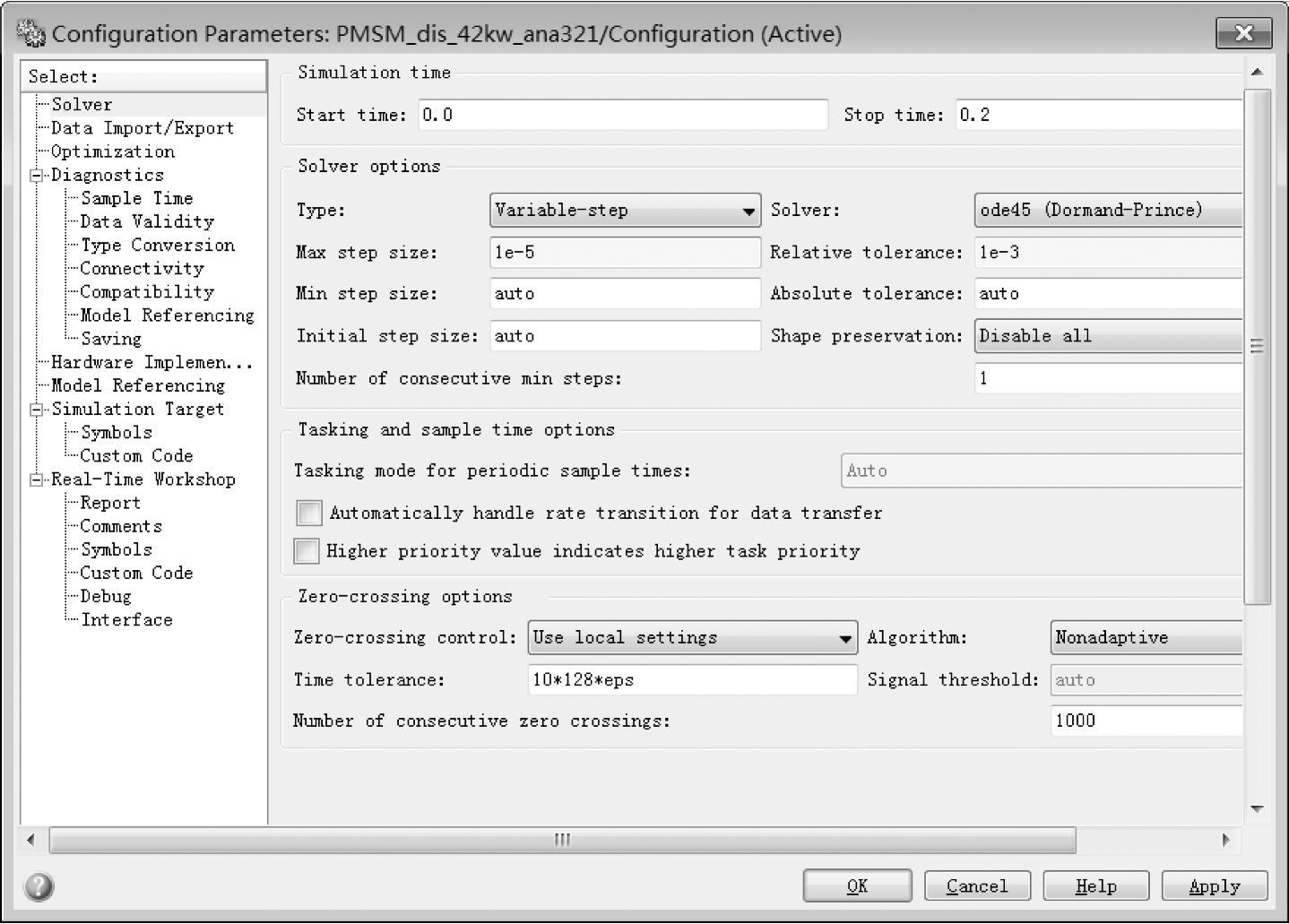
图7-29 修改仿真步长参数设置的对话框

式7-27中的k=427.2-417.8=9.4，σ=-18.7。令t=0.2，那么在MATLAB命令窗口中键入下述指令为

9.4*exp（-18.7*0.2）

可以得到转速增量约为0.22。这与417.5-417.8=-0.3的绝对值是比较接近的。

有几点需要说明：

从对根轨迹的分析中可以发现，电动机在不同负载下工作点的稳定性是不同的。当负载加大时，右半平面极点的实部与虚部都会略微减小。

总的说来，电压型电源供电的同步电动机稳定性较差。如果采用自控式的电流闭环控制，则会大大提高其稳定性能。

本节是将转动惯量作为研究对象，进行了稳态工作点的稳定性分析。同样也可以针对其他的变量，进行稳定性分析。

本节中分析的情况是恒压恒频（Constant Voltage Constant Frequency，CVCF）的电压源，下面两节将分别对变压变频与恒压变频电压源供电下的电动机工作特性逐一分析。