PMSM起动过程分析：探析7.1.2

在第4章中对PMSM进行MATLAB仿真建模中已经对正弦电压供电的小功率PMSM直接起动进行了仿真，其波形如图4-17所示。可以发现，电动机的转矩T_e以及i_q呈现振荡，电动机的转速也呈现振荡，这种起动过程并不理想。

如果针对7.1.1中的大功率隐极式PMSM进行仿真，当负载折算到电动机轴的总转动惯量分别为0.000001、0.0001、0.1三种情况下，前述恒定频率、恒定电压（136V、266Hz）的正弦波供电时，电动机的仿真波形分别如图7-5、图7-6和图7-7所示。三个图中的波形自上而下分别为：电动机转速、电动机转矩、i_d与i_q。

图7-5 转动惯量为0.000001时仿真波形

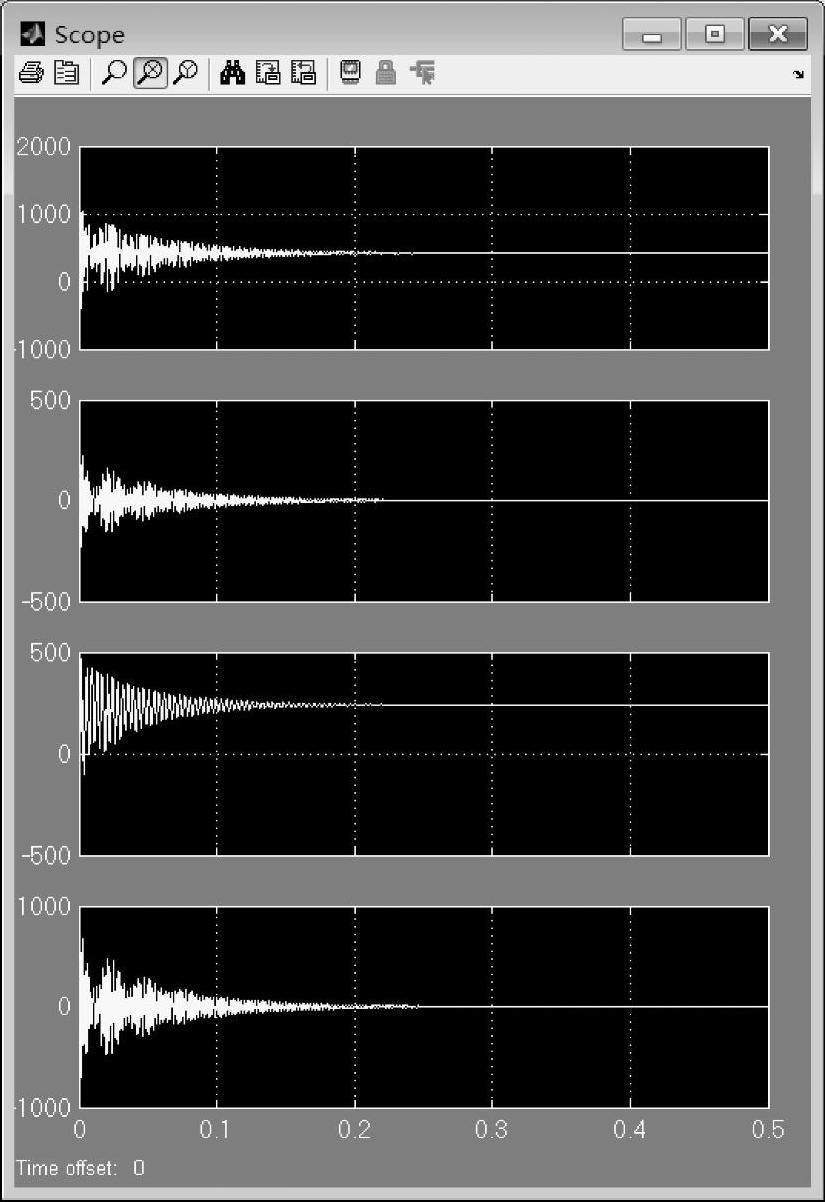
图7-6 转动惯量为0.0001时仿真波形

当电动机转动惯量太小时，电动机转速可以增大到同步速度，但是电动机振荡异常明显，电动机呈现不稳定的振荡，无法稳定运行，如图7-5所示。当电动机转动惯量太大时，电动机速度根本无法加速到同步速度，一直保持在低速振荡，也无法稳定运行，如图7-7所示。只有当电动机转动惯量比较合适时，电动机既能够较快地进入同步状态，又能够稳定的运行，如图7-6所示。

上述分析只是简单的定性分析，下面将定量分析较大转动惯量下电动机的起动电流与转矩。

在较大转动惯量下，电动机的速度来不及在短时间内迅速增加，基本维持在0附近。电动机的起动电流可以按照下式近似计算（这里仍对隐极式电动机进行分析）。

式7-1中的ω₁为电源的电角频率。根据前面的参数可以计算出电动机起动电流大约为740A。这与图7-7中的结果近似。另外，进一步增大转动惯量以保证电动机的转速接近0，得到的仿真波形如图7-8所示。从上到下的四个波形分别是u_d、u_q、i_d和i_q。可以看出在最右侧的i_d与i_q基本上与7-1式计算值接近。

但是在图7-8中还可以看出实际的i_d与i_q的起动过程中的过渡值会大于式7-1的计算值。假定电动机速度ω恒定为0，并且转子位置为0，那么根据两相静止坐标系中电动机的数学模型（见附录A）可以由下式分别计算出i_d与i_q。

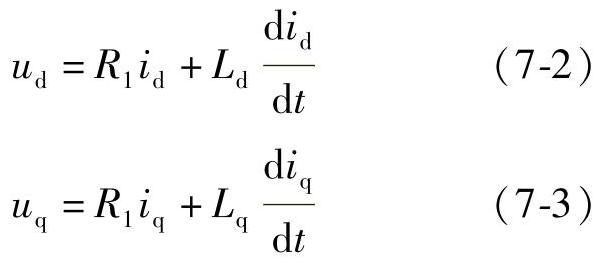
图7-7 转动惯量为0.1时仿真波形(www.xing528.com)

由于R₁很小，忽略R₁的压降，并且将上式改变为积分形式得到

从上式中明显看出，暂态中的定子电流与电压的积分密切相关。如图7-8所示，由于电压矢量的初始相位角是90°，因而t=0时，u_d=0，u_q=u_1m为最大值。根据式7-5分析，可以知道i_q基本上从起动时就进入稳态，这与仿真结果对应。从式7-4和u_d波形可以知道，i_d会经历一个达到最大暂态电流的过渡过程。在0到1/2供电周期内进行式7-4的积分，可以估算出最大暂态电流大约为稳态值的2倍，即接近1480A。图7-8中的仿真数据约为1430A，它们是比较接近的，其差距是由于忽略定子电阻产生的。这里的过渡过程与变压器空载合闸的过渡过程是类似的。

如果需要快速起动隐极式同步电动机，那么需要尽可能快速地增加i_q。从图7-8的图形以及式7-5中可以看出，这就需要对u_q进行适当的控制。如果是电网供电，那么就需要提供一个合适的电压初始相位角。否则，有可能会有负的i_q出现，可能会出现电动机的反转。

下面将定量分析电动机的起动转矩。在第6章推导过电动机的转矩公式6-41，对于隐极式电动机，忽略定子电阻R₁，电动机电流进入了稳态（即不考虑式7-4、7-5的电流暂态），那么可以知道当电动机的转速为ω时，电动机的转矩公式为7-6，式中的相角γ为电压矢量超前转子d轴的电角度。

图7-8 大惯量（J=100）电动机的起动仿真波形

注意：由于惯量大的电动机转速来不及增加很多，所以在dq坐标系中，电压矢量是一个高速旋转的电压矢量。所以γ也在快速、周期性变化而不能稳定下来，这就表明电动机的转矩也是一个高速振荡的变量，其频率主要由电压频率决定，另外还包含了电动机转速的低频振荡。从图7-9中容易看出振荡情况，图中自上而下4个波形分别是电动机转速、电动机转矩、i_d和i_q。

图7-9 转动惯量J=0.1、电压矢量初始相角为0时的仿真波形

从式7-6中可以看出，电动机的起动转矩近似按照电压角频率高速振荡。如果在转矩为正值的半个周期内电动机的速度有明显的增加，那么经过几个周期，电动机就有可能进入同步速度运行。这类似于图7-6的起动过程。

不过在实际系统中，与大功率电动机相对应的机械系统的转动惯量也是比较大的，所以实际系统是难以直接起动的。这就是同步电动机调速系统的起动难题。传统的解决方法是在转子中加入阻尼绕组，电动机可以按照等效异步电动机起动，最后转入同步电动机方式运行于同步速度。另一种解决方法是采用一台原动机拖动同步电动机，将其转速提高至接近同步速度，然后投入工频交流电再进行起动。此时根据式7-6可知，只要两个速度较为接近，以及电压相位角控制比较合适，那么电动机可以达到同步速度。

顺便说说转子阻尼绕组的作用，它除了在起动中发挥作用，还可以提高同步电动机在同步速度下的运行稳定性，力图使电动机保持在同步速度而不偏离。而一旦进入同步速度运行后，阻尼绕组就没有基波感应电流和相应的转矩了。