PMSM稳态工作特性分析

为简化公式的推导，分析中假定L_d=L_q=L，即暂不考虑电动机的凸极效应。首先分析当恒定电压与恒定频率的正弦交流电压源供电下PMSM的稳态工作特性，MATLAB程序如下：

MATLAB程序运行后得到如图7-1所示的图形。其中横坐标是电动机的输出转矩，其范围从0到220Nm。红色曲线1是定子电流的相位角，蓝色曲线2是定子电流幅值，蓝色曲线3是电压矢量的相位角，绿色曲线4是功率因数波形，其纵坐标见图形右侧。

由于电动机的定子电阻非常小，这里忽略，所以电压的公式会简化一些。另外，由于不考虑凸极效应，电动机的转矩仅包含了永磁转矩，转矩公式也大为化简。

图7-1 恒定电压与恒定频率下正弦交流电压源供电环境下PMSM的稳态特性

从图7-1中可以看出，在较小的转矩输出下，电动机电流工作在第一象限，即定子电流励磁分量产生了增磁的效果，实际上这是不需要的。另外，电动机的功率因数很低。所以图7-1表明当输出转矩较小时，采用恒定电压模式并不适合。换句话说，电动机并不需要如此高的电压，否则电动机的工作特性并不理想。

从图7-1中可以看出，在较大的输出转矩下，例如接近180Nm时，电动机的电流矢量逐步进入第二象限（δ＞90°），电动机的功率因数普遍较高，但是电动机的电流幅值增加非常明显。因为转矩的输出需要有相应大小的i_q，从而要求了较大的定子电流幅值。

图7-2给出了上述分析中电动机在电流相平面中的工作点。恒定电压和恒定频率下，图中的电压圆是固定不变的。电动机的恒转矩曲线是与横轴平行的，所以当电动机转矩逐步增加时，电动机的工作点从图中的A₁逐步移动到A₂、A₃等等，最大转矩对应了工作点A₆。电动机的工作点从第一象限逐步移动到第二象限。

(www.xing528.com)

图7-2 电流相平面中的电动机工作点

上述分析的PMSM与传统的隐极式电励磁同步电动机特性是相同的，它们的唯一区别就在于磁场是永磁体产生的还是直流励磁绕组产生的。

如果考虑到PMSM的凸极效应，电动机参数同42kW电动机，此时电动机的磁阻转矩明显较大，因而与上述的隐极式电动机的特性大不相同。由于转矩公式比较复杂，可以借助半角正切公式进行MATLAB分析，得到图7-3的曲线。图7-3中的虚线与实线分别对应了隐极式与凸极式PMSM的特性曲线。蓝色曲线1、2对应了电流幅值（取530A为基值进行了标幺化处理），黑色曲线3、4对应了电压矢量的相位角（按照180°进行标幺化处理），紫色曲线5、6对应了功率因数，红色曲线7、8对应了电流矢量的相位角（按照180°进行标幺化处理）。可以看出，对于输出相同的转矩，凸极式电动机由于多了磁阻转矩分量，定子电流需求较少，并且功率因数相对较高。这样，电动机定子铜耗减少，功率因数提高，降低了电源容量的需求。

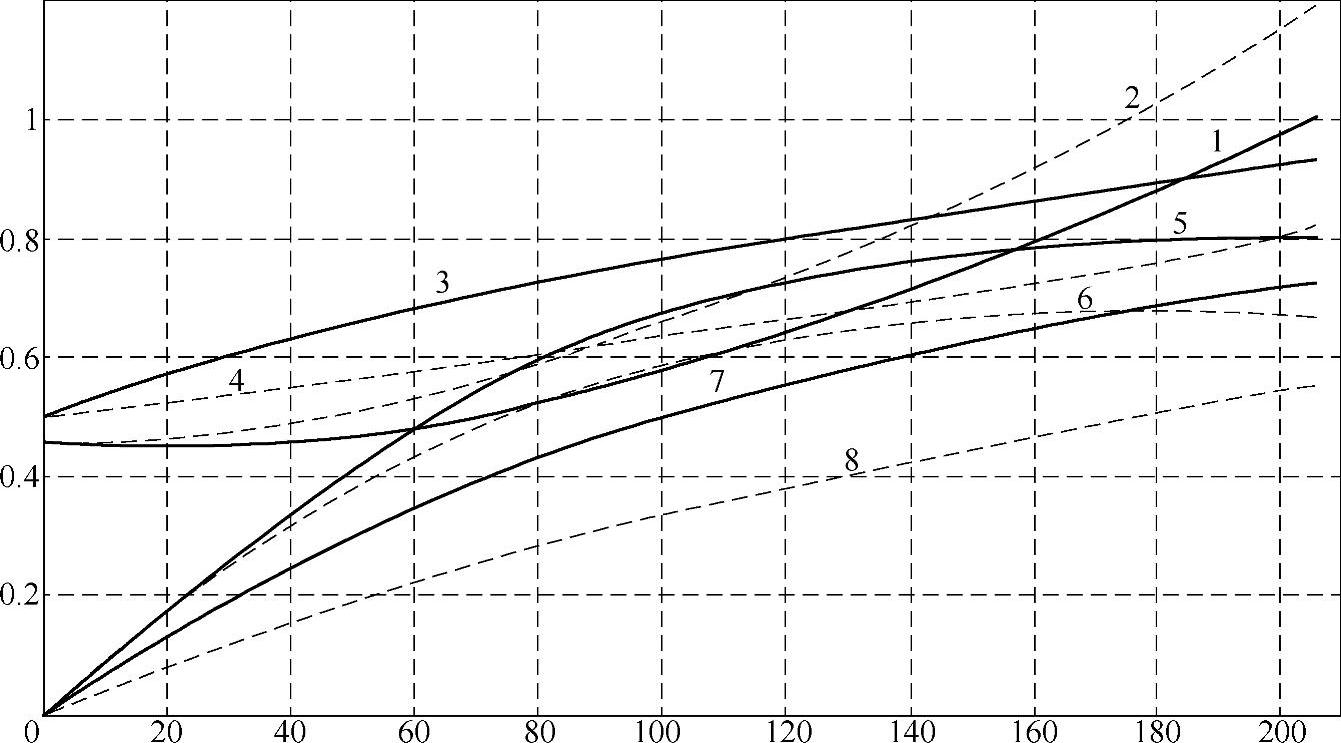
图7-3 恒定电压与恒定频率下正弦交流电压源供电凸极PMSM的稳态特性

从图7-4的电动机电流工作点可以看出隐极式电动机与凸极式电动机工作点的不同，图中的虚线与实线分别对应了隐极式与凸极式PMSM电动机。图中电压圆变成了电压椭圆，水平的恒转矩曲线变成了实线的双曲线（这里只绘出了其中的一簇），它们的一些列交点对应了不同输出转矩下的电动机工作点。例如，A₁点是电动机空载时的工作点，实线与虚线是重合的。随着转矩的不断提升，虚线的工作点明显成比例提高，电流需求较大；实线的工作点在上升的同时向左移动，因为有较高的磁阻转矩，故而对i_q的需求降低了。总的说来，在同一个转矩输出下，凸极电动机的定子电流幅值降低了。

此外，图7-2中工作点A₆移动到电压圆的最高点，这对应了i_q的最大点，即最大输出转矩点。但是在图7-4中，电压椭圆的最高点同样是i_q最大点，但并不是最大转矩输出点。

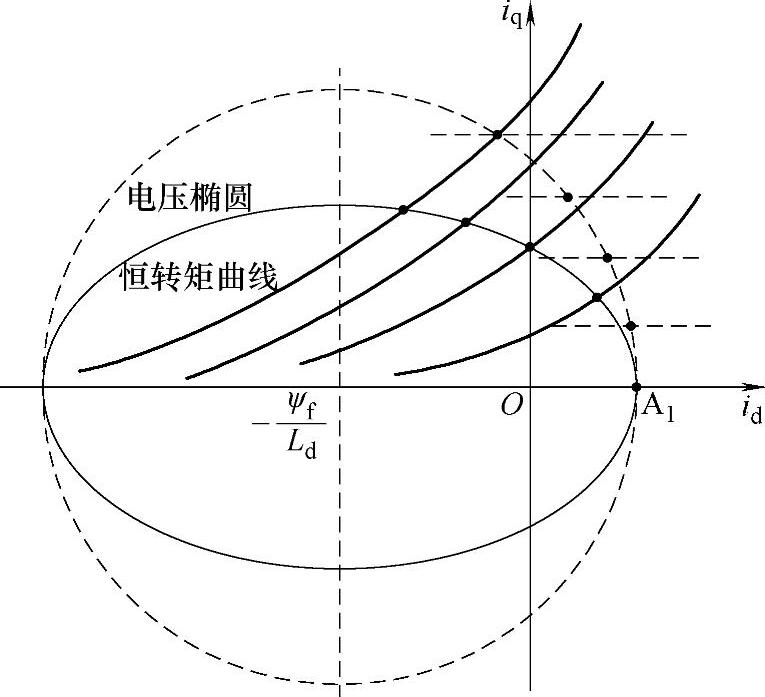
图7-4 电流相平面中的隐极式与凸极式电动机工作点对比