电动机功率因数的计算与控制中的id及iq的关系分析

以图6-14为例，电动机的功率因数可以用下式计算为

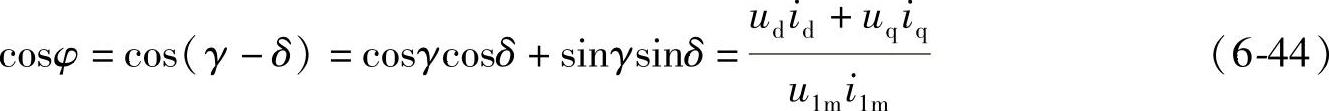
当忽略定子电阻时，式6-44可以描述为式6-45。

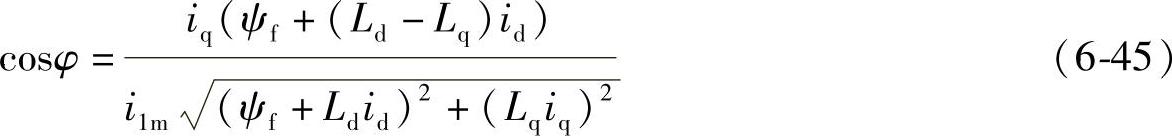
从式6-45中可以容易看出，电动机的功率因数与电动机控制中的i_d及i_q密切相关。为了控制电动机的转矩，在采用不同的电流工作点（i_d，i_q）时，对应的电动机功率因数都不相同。

例如，当采用i_d=0时，式6-45可以改写为

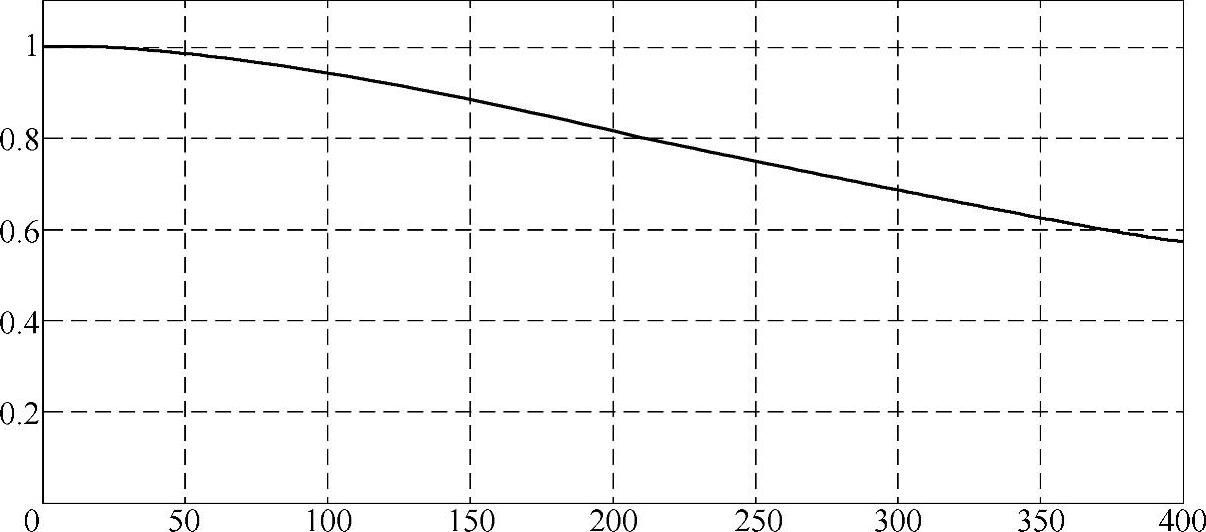
将式6-46绘制成图形，如图6-19所示，可以看到在i_d=0的控制中，随着转矩（或者说i_q）逐渐增加的过程中，电动机的功率因数会有明显的下降。在一定的功率下，功率因数的下降会提高电动机对定子电压的需求，即要求电源能够提供更高的电压，所以对电源装置提出了更高的要求。

(www.xing528.com)

图6-19 功率因数随i_q变化曲线

当电动机运行于电压受限的恒压情况时，根据式6-11、式6-12来计算式6-46中的i_d、i_q以及电流峰值i_1m。此时对于电压相位角在90°～180°范围内变化时的功率因数变化情况绘制成曲线，如图6-20所示。图中绘制了不同转子速度下的功率因数曲线，转速范围是4000～12000r/min。可以看出，在靠近左侧的范围内，电动机弱磁程度较小，此时的功率因数也较小。随着电压相位角的增加，电动机弱磁程度增加，功率因数增大。另外在图中较低速度时，可以进一步加大弱磁程度，此时电动机的电压未必达到限制，故而其功率因数可以大大高于图中的相应曲线。

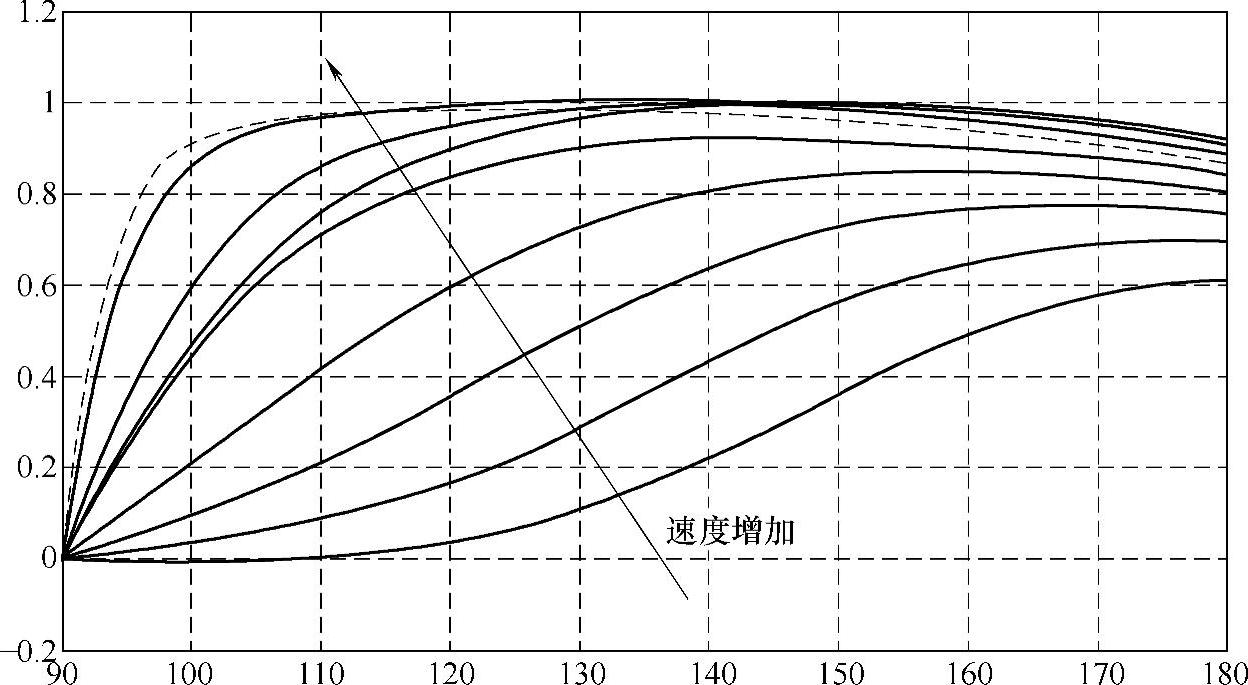
图6-20 功率因数随电压相位角的变化情况

上述分析中的MATLAB程序如下：

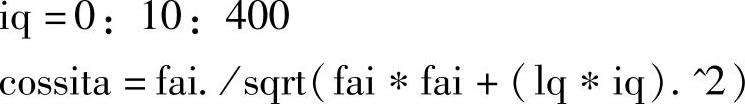
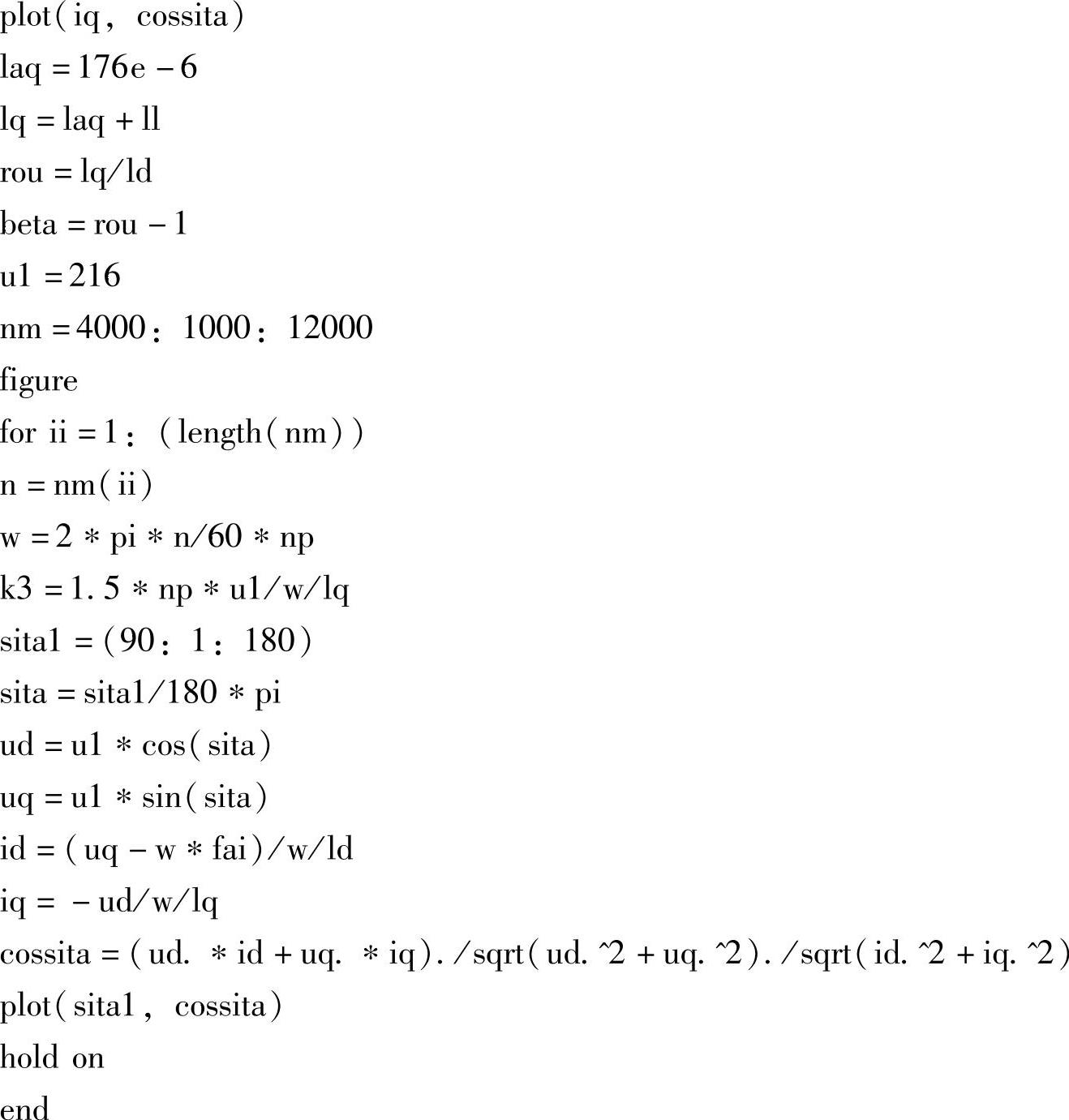
在上述分析中，可以看出电动机的功率因数与控制策略关系甚大。