PMSM的电磁转矩是我们最为关心的一个物理量,参考公式3-42,可以得到转矩公式如下
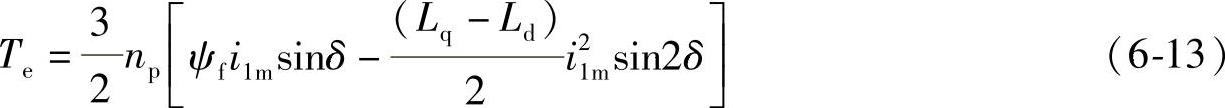
式中的δ是定子电流矢量超前d轴的角度,该角度称为转矩角,又称负载角。一般情况下,电动机控制中常用的电流矢量是在q轴上和第二象限内的。
公式6-13内的电动机转矩包含了两项,前者为永磁转矩——永磁体与定子电流作用的结果,这一部分定子电流仅仅是指iq。后者为磁阻转矩——由于dq轴的磁路不对称产生的电磁转矩,它与iq及id都成正比例。图6-4中给出了典型的PMSM转矩与转矩角关系曲线,称为矩角特性曲线。图6-4中1为永磁转矩,显然其最大值出现在90°。图6-4中曲线2为磁阻转矩。由于PMSM中的Ld<Lq,使得在δ>90°时,磁阻转矩才出现正值。对于传统的电励磁同步电动机来说,磁阻转矩的情况刚好相反。图6-4中曲线3给出了总的转矩,其特点是δ>90°时出现转矩的最大值。为了得到较大的转矩并运行在较高速度下,PMSM的转矩角一般控制在δ≥90°的范围内。
从图6-4可以看出由于δ的不同,PMSM可以产生不同的转矩。那么可以设想,为了得到相同的转矩,完全可以由不同幅值的定子电流来产生。为此,针对第3章42kW的PMSM进行分析,MATLAB程序如下:

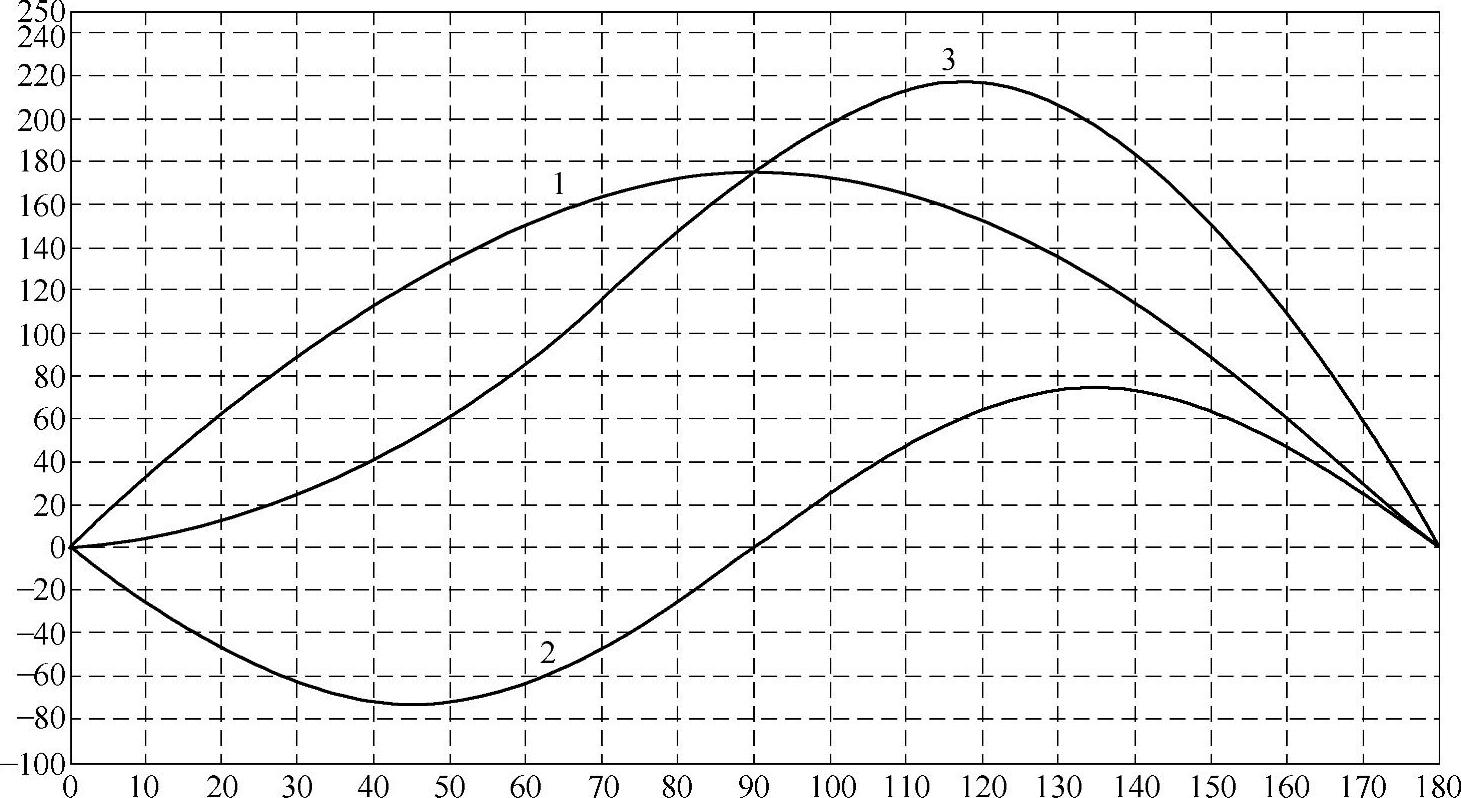
图6-4 典型矩角特性图
运行上述程序后,可以得到图6-5所示的不同电流幅值对应下的PMSM矩角特性曲线。显然,随着电流的增加,产生最大转矩的负载角也略微发生变化。为了产生同一个转矩,确实存在不同的电流幅值及负载角。
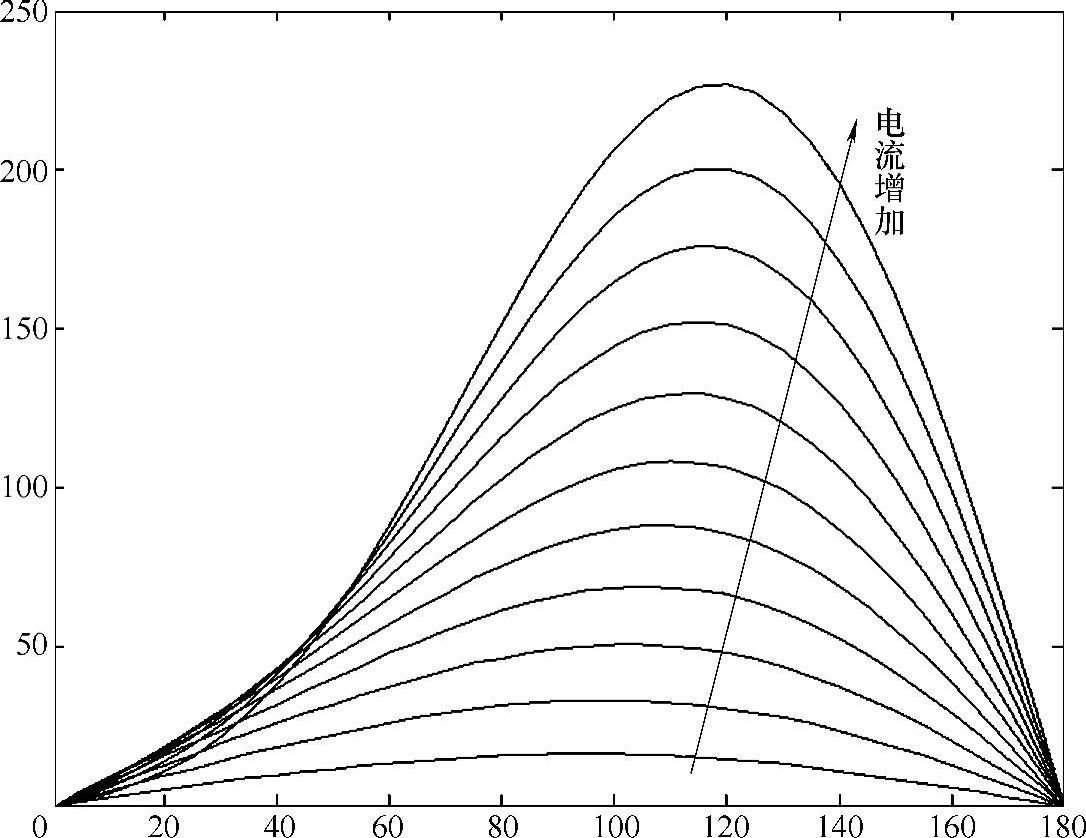
图6-5 不同电流下的矩角特性曲线图
下面针对某定子电流幅值下的最大转矩值进行分析。此时式6-13中的电流i1m不变,转矩仅仅随δ变化,为求Te极值,令其导数为0,如6-14式

从而可以得到式6-15
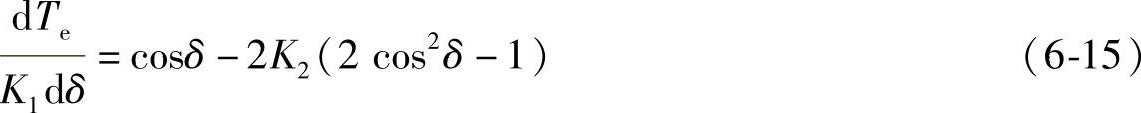
上式中的相关系数分别见式6-16和式6-17。

式6-17中的变量ρ为电动机的凸极率,见式6-18所示,对于PMSM,存在ρ≥1。

设置新变量β见式6-19,
β=ρ-1 (6-19)
这样,式6-17可以改写为式6-20。

令式6-15为0,那么可以得到式6-21,
4K2cos2δ-cosδ-2K2=0 (6-21)(https://www.xing528.com)
进而,可以求得

根据前述的分析,式6-22所示的余弦值应该为非正,因此最终得到式6-23。

相应地,有
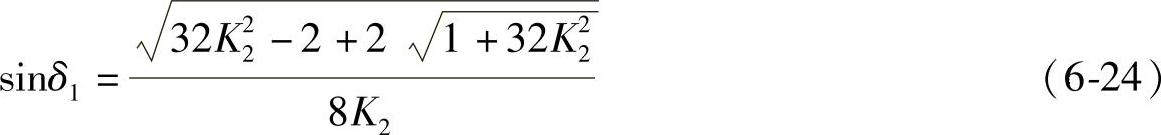
将式6-23与6-24代入式6-13,可以得到最大转矩为
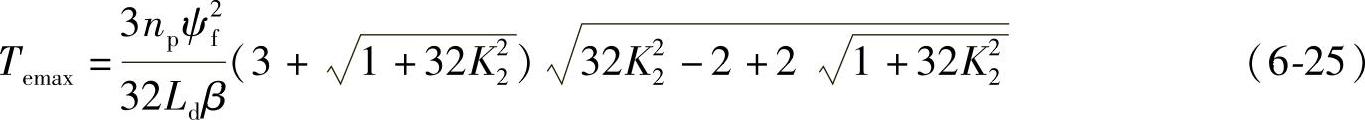
设置新变量Kf如下

那么K2可以表示为

首先,可以分析凸极率ρ趋近于1的情况,那么此时β趋近于0。由式6-23可以得出δ1趋于90°,由式6-25化简可以得到式6-28。该式即为表面贴装式PMSM的转矩公式,因为该电动机中,id不产生转矩,所以6-28的结论是显而易见的。

针对凸极PMSM(ρ>1,亦即β>0),下面进一步分析最大转矩的特征。对PMSM而言,永磁磁链与Ld一般不会明显变化,因而从式6-25中可以看出,最大转矩与β以及Kf关系密切。
图6-6给出了最大转矩与Kf关系,其中β为参变量。图6-6中四条曲线从下到上分别对应了β=0、β=1、β=2和β=3的情况。当β=0时,转矩与Kf是一种线性关系。
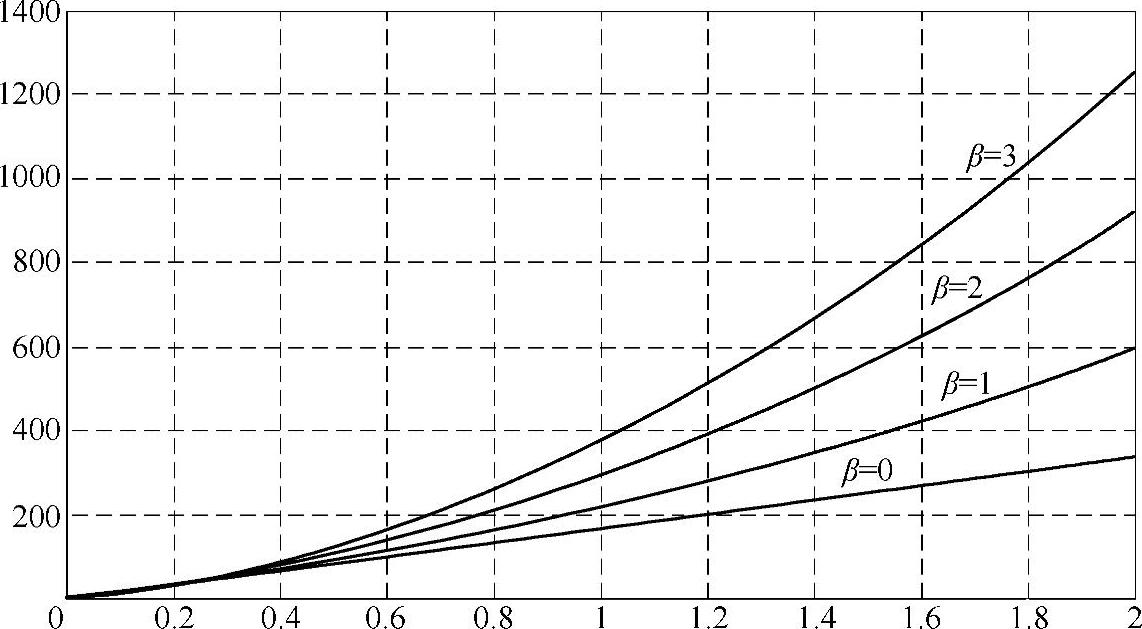
图6-6 最大转矩与Kf关系(β为参变量)
图6-7给出了最大转矩与β关系,其中Kf为参变量。图中7条曲线从下到上分别对应了Kf=0、Kf=0.2、Kf=0.4、Kf=0.6、Kf=0.8、Kf=1.0、Kf=1.2的情况。可以看出,在电动机相电流峰值不变的情况下(即Kf恒定),最大转矩会随着β的增加而增大。这就是说,如果电动机的相电流有限制的话,那么增加电动机的凸极率,可以提高电动机的最大转矩输出能力。另外,图6-7便于对比分析一定幅值、不同相角时的定子电流矢量产生的电动机转矩。由于电流相角不同,那么id、iq均不同,此时电动机的相电感也会随着电流发生变化。利用图6-7则可以非常方便地分析转矩输出能力与β的关系,因为此时的参变量Kf不变。
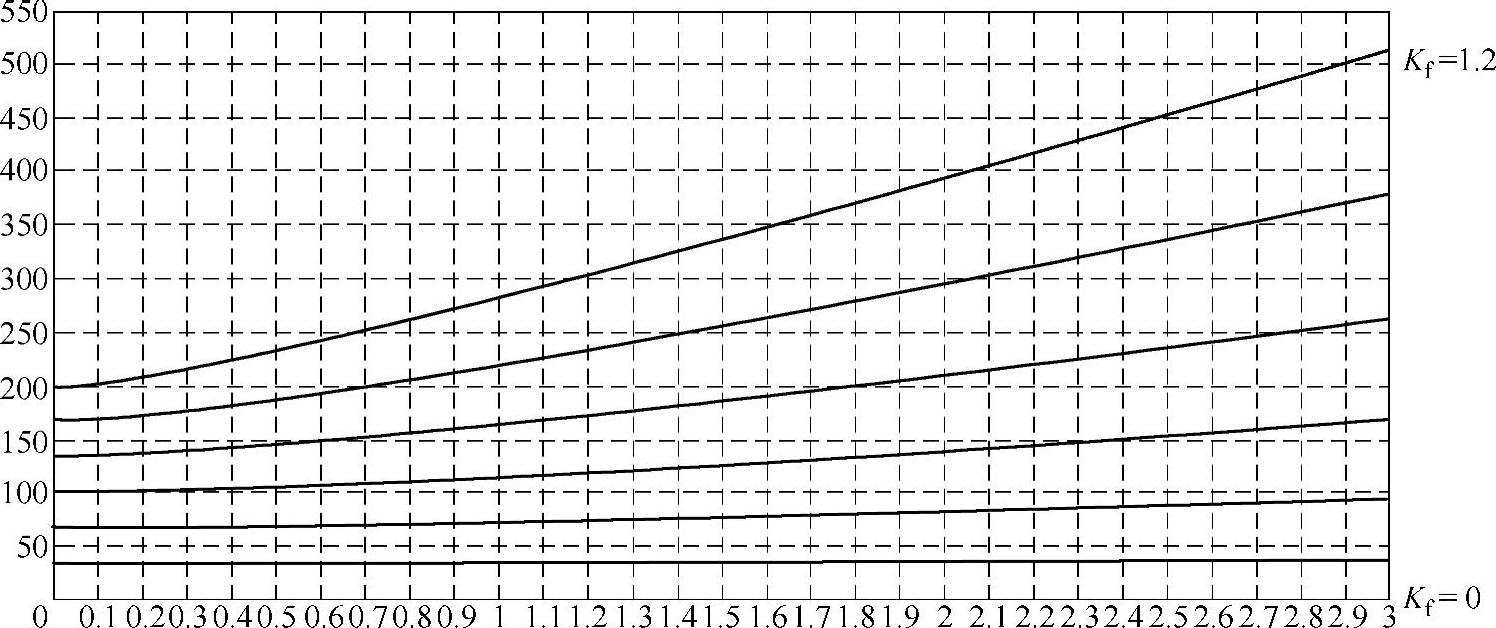
图6-7 最大转矩与β关系(Kf为参变量)
上述分析中的MATLAB部分程序如下:
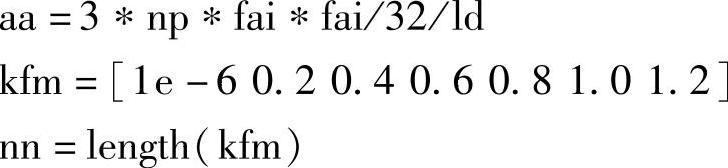
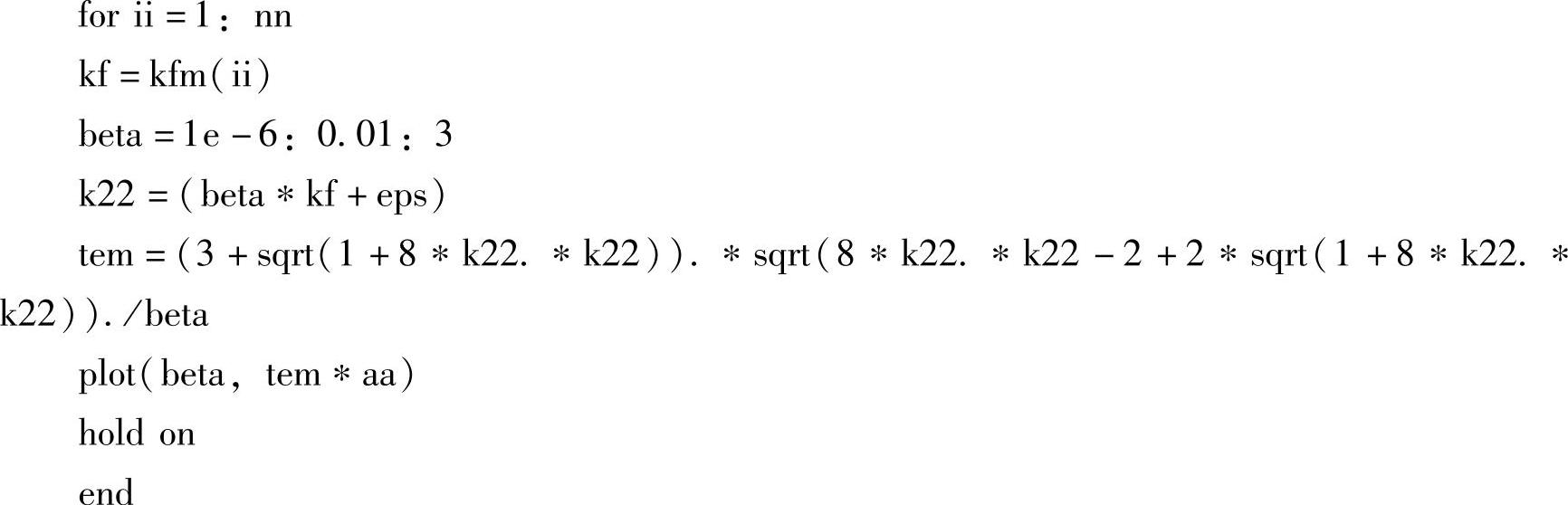
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




