电压极限椭圆优化：电压极限椭圆分析方法简述

稳态工况下，PMSM定子电压为

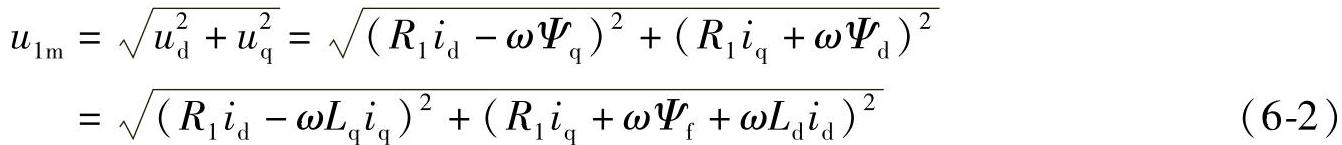
讨论电动机在高速运行时，定子电阻压降较小，与感抗上的压降相比可以忽略。所以近似有

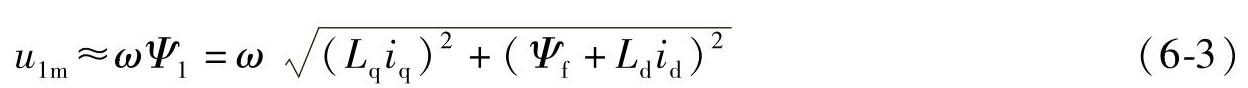
这就是电动机运行于较高速度下的定子电压幅值公式，可以看出在保证定子电流分量（i_d，i_q）不变的情况下，随着电动机运行速度的提高，定子电压会随之上升，那么最终将会达到电压极限（逆变器输出能力以及电动机绝缘能力等的限制）。

根据式6-3可以推出电动机定子电压一定时，电动机直轴电流与交轴电流所满足的规律如下：

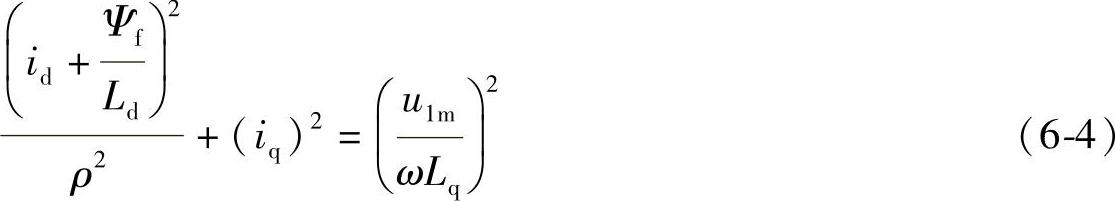
上式中，当方程右边为一个常数时，定子电流的两个分量在相平面上的图形是一个椭圆，如图6-2所示。由于凸极率ρ=L_q/L_d＞1，椭圆在d轴上两个焦点间的距离比q轴上的大。当ρ为1时，椭圆变成了圆。

实际PMSM调速系统的主电路中采用电压型逆变器向永磁同步电动机供电，所以电动机的运行性能受到逆变器输出能力的限制。在逆变器直流侧电压为U_d时，定子线电压基波峰值最大为U_d，所以逆变器输出给电动机定子相电压峰值可以达到U_lim。

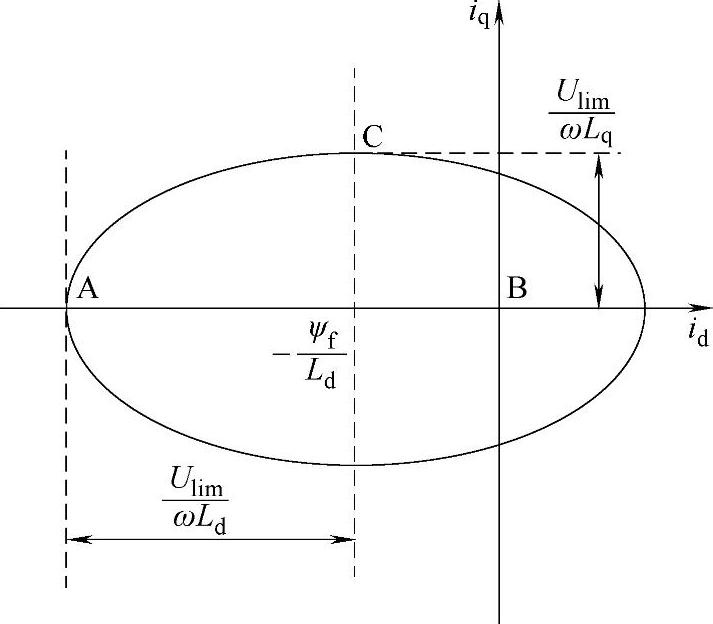
图6-2 定子电压极限椭圆

下面考虑当电动机转速上升到较高（ω_r1）时，式6-4右边的定子电压u_1m达到了U_lim而不能继续增加时的情况。此时定子电压保持为一个常数，所以随着转速的增加，方程右边的值慢慢减小，这样就对应着一系列不同的电压椭圆曲线，如图6-3所示。

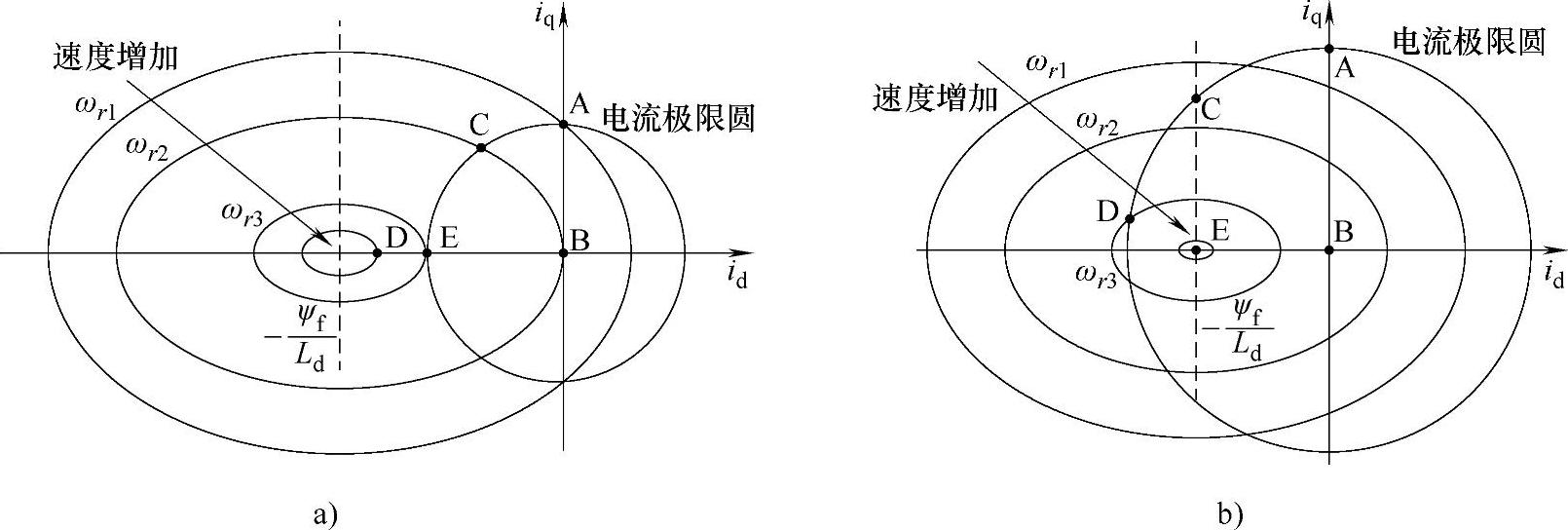
图6-3 不同速度下的定子电压极限椭圆(www.xing528.com)

a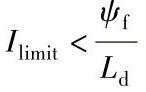） b）

受到电压限制的电动机的工作点可以设置在电压极限椭圆的边界和其内部。从图6-3中可以看出，如果按照i_d=0进行控制，那么在定子电压极限下，随着转速的增加，图中的工作点只能从A到B，最后工作点在原点，达到此时的最高转速ω_r2。令i_d=0，从式6-4可以推出

在原点处的ω_r2为

需要说明的是，式6-7给出的是理想空载运行工况下的最高速度，如果带负载运行，那么电流i_q不能为0，所以实际运行最高转速将会比ω_r2小。

在直流电动机中可以通过磁场削弱来进行转速的提升。对于交流永磁电动机，由于励磁采用永久磁体励磁不能像电励磁那样可以方便地调节励磁磁动势，但是可以通过控制定子电流的励磁分量i_d，使其产生削弱气隙磁场的效果。

根据式6-4知道：当i_d为负值进行弱磁控制时，在同一个i_q与转速情况下，公式左边的数要更小，所以右侧的定子电压需求u_1m会更小。这即是说，进行弱磁控制时公式右侧更小，所以定子电压维持恒定情况下的电动机转速可以进一步提升。

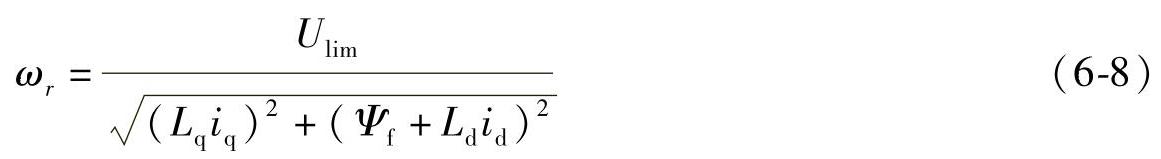
对应图6-3，定子电压达到极限后采用弱磁控制时，工作点将会从A到C进而到D。但是如果考虑到逆变器输出的电流极限，那么最终能够达到的速度将根据电流极限与电压极限共同确定为E点。对于理想空载情况下i_q=0，那么可以求得最高转速ω_r3为

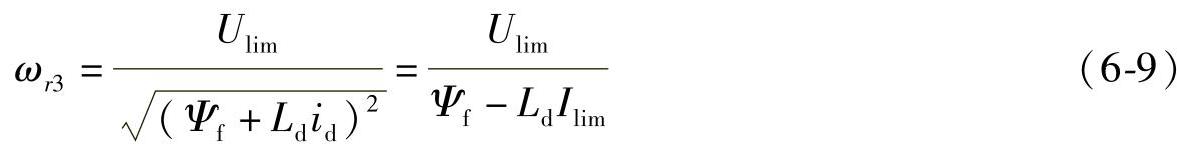
但是对于电动机负载运行的工况来说，运行的最高转速比ω_r3要小一些。

从式6-9看出：如果逆变器输出电压和电动机定子允许电压可以增加的话，那么极限速度ω_r3可以增加；另外如果直轴电感增加的话，那么ω_r3也可以增加。所以在运行中，为了得到更高的电动机转速，有时在定子回路串接电感来增加等效L_d，目的是可以进一步提速。

从图6-3中还可以看出，如果定子电流允许值较大，那么会出现电压极限椭圆的中心会在电流极限圆的内部。这即是说，存在这样的情况，定子电流弱磁分量足够大，理论上可以完全抵消永磁磁场。从式6-9可以看出，在空载情况下，转子速度理论值可以是无穷大。当然在实际调速系统中，一般不会出现这种情况，为了保证电动机永磁体的正常工作，弱磁的程度是需要控制的。