定子磁链方程的计算方法

三相定子绕组的全磁链（ψ₁（θ，i））可以表示为

（ψ₁（θ，i））=（ψ₁₁（θ，i））+（ψ₁₂（θ）） （3-2）

其中（ψ₁₂（θ））矩阵是永磁体磁场匝链到定子绕组的永磁磁链矩阵。

ψ_fA（θ）、ψ_fB（θ）、ψ_fC（θ）分别为永磁体磁场交链A、B、C三相定子绕组的永磁磁链分量（Wb），与定子电流无关。对于一台确定的电动机，永磁磁链仅与转子位置θ有关。

式3-2中的（ψ₁₁（θ，i））是定子绕组电流产生的磁场匝链到定子绕组自身的磁链分量：

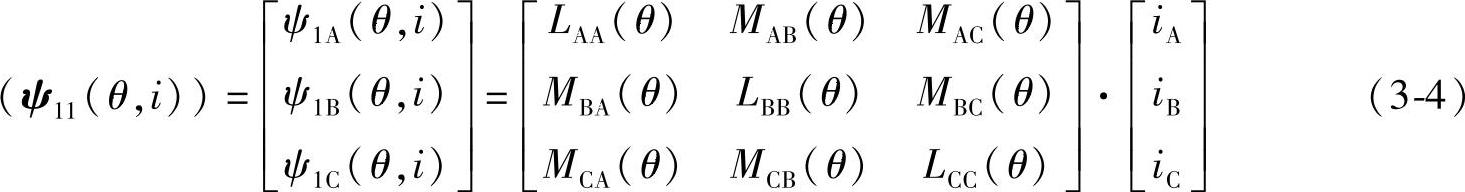
式中 L_AA、L_BB、L_CC——三相定子绕组的自感（H）；

M_AB、M_AC、M_BA、M_BC、M_CA、M_CB——三相定子绕组之间的互感（H）。

下面对式3-4中的电感系数分别进行分析。

1.定子绕组的漏自感和自感

永磁同步电动机定子绕组中通入三相电流后，由电流产生的磁通分为两部分：一部分为漏磁通，与漏磁通相对应的电感与转子位置无关，为一个恒定值；另一部分为主磁通，该磁通穿过气隙且与其他两相定子绕组交链，当电动机转子转动时，凸极效应会引起主磁通路径的磁阻变化，对应的电感系数也相应发生变化。在距离d轴角度为θ的点Q处，单位面积的气隙磁导λ_δ（θ）可以足够精确地表示为

λ_δ（θ）=λ_δ0-λ_δ2cos2θ （3-5）

式中 λ_δ0——气隙磁导的平均值；

λ_δ2——气隙磁导的二次谐波幅值。

公式3-5描述的气隙磁导与转子位置角θ之间的关系描绘在图3-3中。当θ=0°时，d轴方向气隙磁导为

λ_δd=λ_δ0-λ_δ2 （3-6）

当θ=90°时，q轴方向气隙磁导为

λ_δq=λ_δ0+λ_δ2 （3-7）

注意，式3-5、3-6、3-7与电励磁同步电动机的公式略有不同，因为两类电动机中d、q轴的气隙磁导规律不同（永磁同步电动机中，d轴电感小于或者近似等于q轴电感，电励磁同步电动机则反之）。为了更加符合PMSM情况，将公式略作修改，但并不影响最终推导的d、q轴电感以及磁链和转矩方程的表达式。

所以可以得到

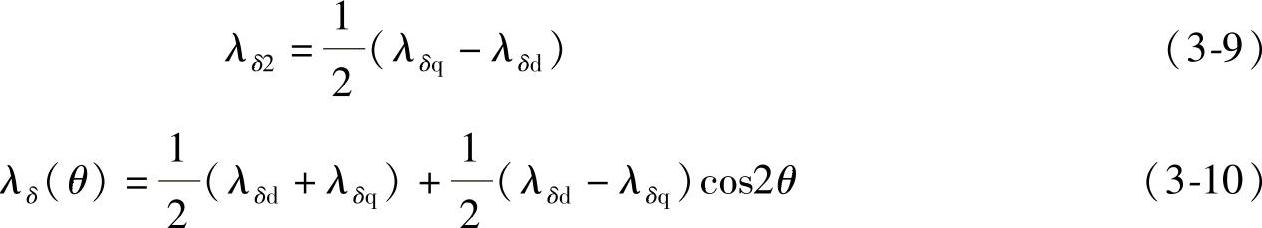
为了对比的更加清楚，图3-3中还绘制了定子绕组三相电流的示意图。这三相电流在转子位置从0°到360°的变化过程中都呈现一个周期的变化，在此过程中，因而气隙磁导出现了两个周期。

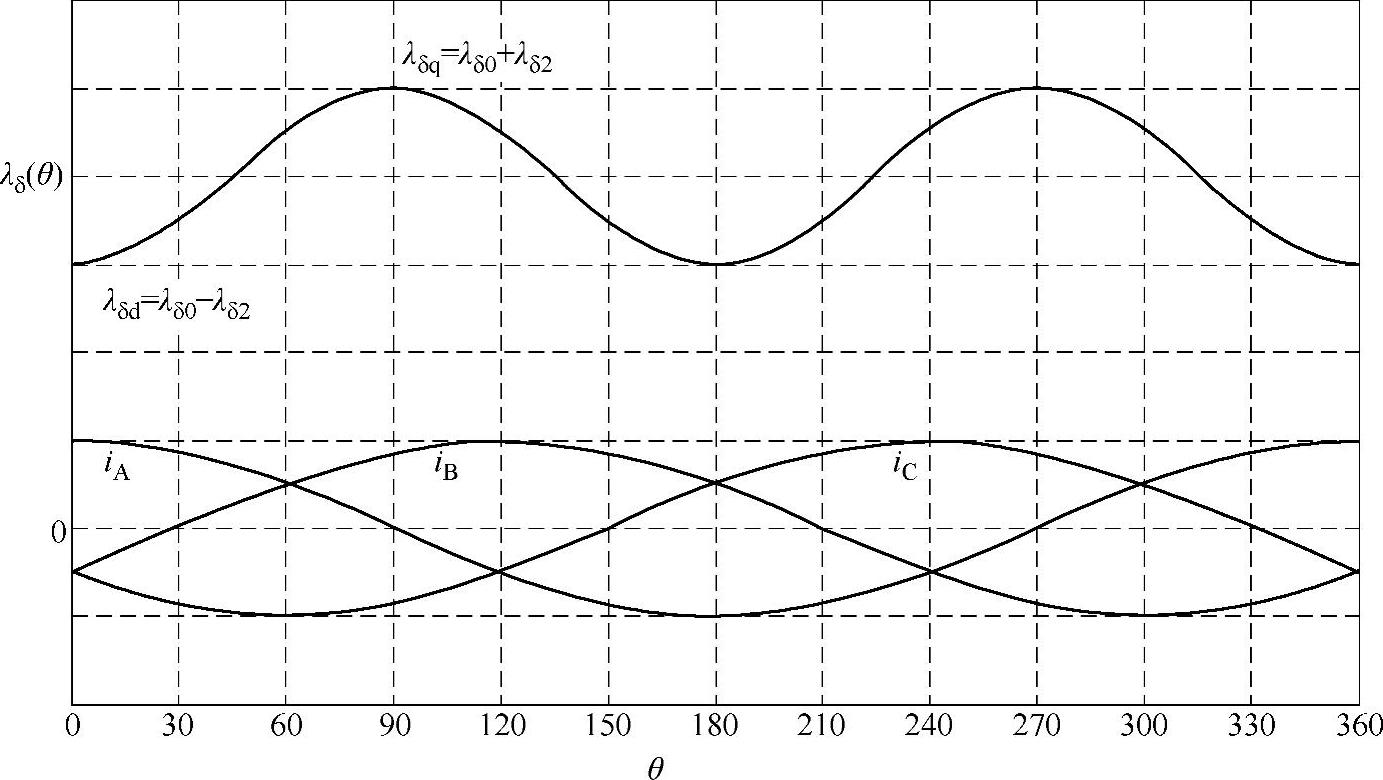
图3-3 气隙磁导波形图

另外，图3-3中所示的三相定子电流中仅含有励磁分量（d轴分量），不含有转矩分量（q轴分量）。若希望电动机能够输出非零转矩，那么图中的电流相位必须发生改变。结合后面的转矩公式可以更好地理解这一点。

以A相定子绕组为例，当通入电流i_A时，在A相定子绕组轴线方向的磁动势F_A与Q点处单位面积的气隙磁导λ_δ（θ）对应的A相定子绕组气隙磁链ψ_Aδ（θ）满足如下关系：

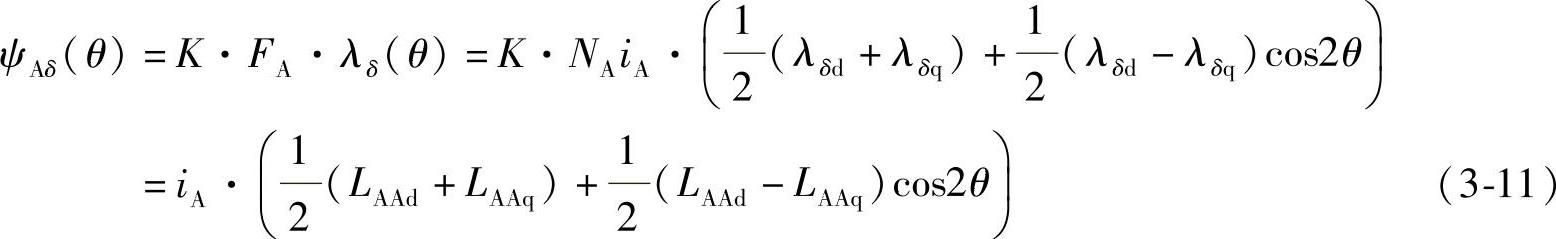
式中 K——气隙磁链和磁动势、气隙磁导的比例系数；

N_A——A相绕组的匝数。且L_AAd=K·N_A·λ_δd，L_AAq=K·N_A·λ_δq。

根据漏自感和自感的定义，A相定子绕组的漏自感L_Aσ和自感L_AA分别表示为

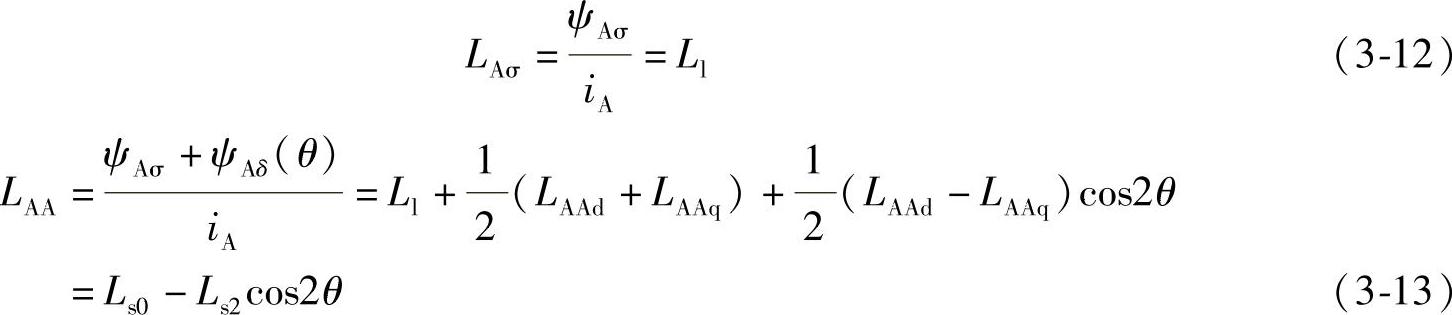
两式中，L_l为漏自感的平均值，与A相定子绕组漏磁链ψ_Aσ有关，与转子位置无关；L_s0为A相定子绕组自感的平均值，L_s2为A相定子绕组自感二次谐波的幅值。可以看出，有以下关系式成立

L_s0=L₁+（L_AAd+L_AAq）/2 （3-14）

L_s2=（L_AAq-L_AAd）/2 （3-15）

由于B相定子绕组和C相定子绕组与A相定子绕组在空间互差120°，可以认为A、B、C三相定子绕组各自的漏电感相等，即有

L_Aσ=L_Bσ=L_Cσ=L_l （3-16）

因而将式3-13中θ分别用（θ-120°）和（θ+120°）替代，可以求得A、B、C三相定子绕组的自感为(www.xing528.com)

L_AA=L_s0-L_s2cos2θ

L_BB=L_s0-L_s2cos2（θ-120°）

L_CC=L_s0-L_s2cos2（θ+120°） （3-17）

2.定子绕组的互感

当A相定子绕组通入电流i_A时，在A相定子绕组轴线方向的磁动势F_A可以分解为d轴方向的直轴磁动势分量F_Ad和q轴方向的交轴磁动势分量F_Aq。

F_Ad=N_A·i_Acosθ

F_Aq=N_A·i_Asinθ （3-18）

直轴磁动势分量F_Ad和交轴磁动势分量F_Aq分别产生各自的磁链分量ψ_Ad（θ）和ψ_Aq（θ）为

ψ_Ad（θ）=K·F_Ad·λ_δd=K·N_Aλ_δd·i_Acosθ

ψ_Aq（θ）=K·F_Aq·λ_δq=K·N_Aλ_δq·i_Asinθ （3-19）

由于d轴与B相定子绕组轴线相差（θ-120°），ψ_Ad（θ）与B相定子绕组交链的部分为ψ_Ad（θ）cos（θ-120°）；ψ_Aq（θ）与B相定子绕组交链的部分为ψ_Aq（θ）sin（θ-120°）；因此，A相定子绕组电流i_A经过气隙与B相定子绕组交链的磁链ψ_BAδ（θ）表示为

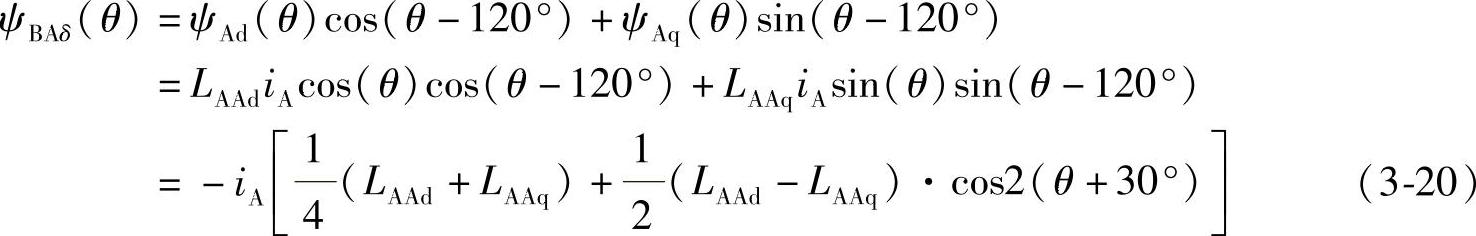
A相定子绕组与B相定子绕组的互感M_BA可以表示为

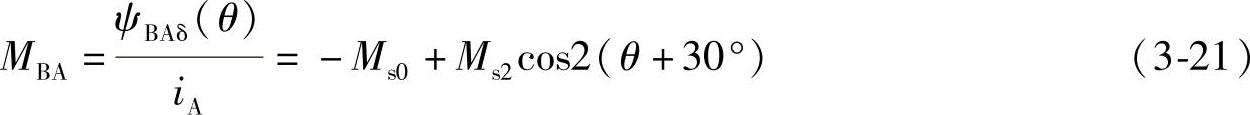
式中 M_s0——A相、B相定子绕组互感平均值的绝对值；

M_s2——A相、B相互感的二次谐波的幅值。

它们满足

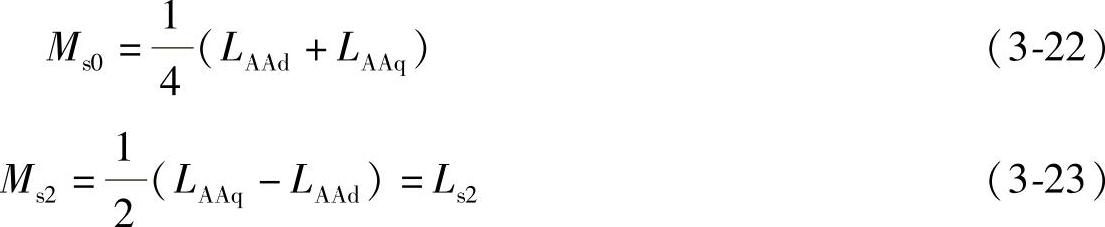
由于空间的对称性，当B相定子绕组通入电流i_B时，B相定子绕组与A相定子绕组的互感可表示为

M_AB=-M_s0+M_s2cos2（θ+30°） （3-24）

因而将式3-20和3-21中的θ分别用（θ-120°）和（θ+120°）替代，可以得到A、B、C三相定子绕组的互感为

M_AB=M_BA=-M_s0+M_s2cos2（θ+30°）

M_BC=M_CB=-M_s0+M_s2cos2（θ-90°）

M_AC=M_CA=-M_s0+M_s2cos2（θ+150°） （3-25）

将式3-17、式3-25代入式3-4定子磁链分量的矩阵方程可得：

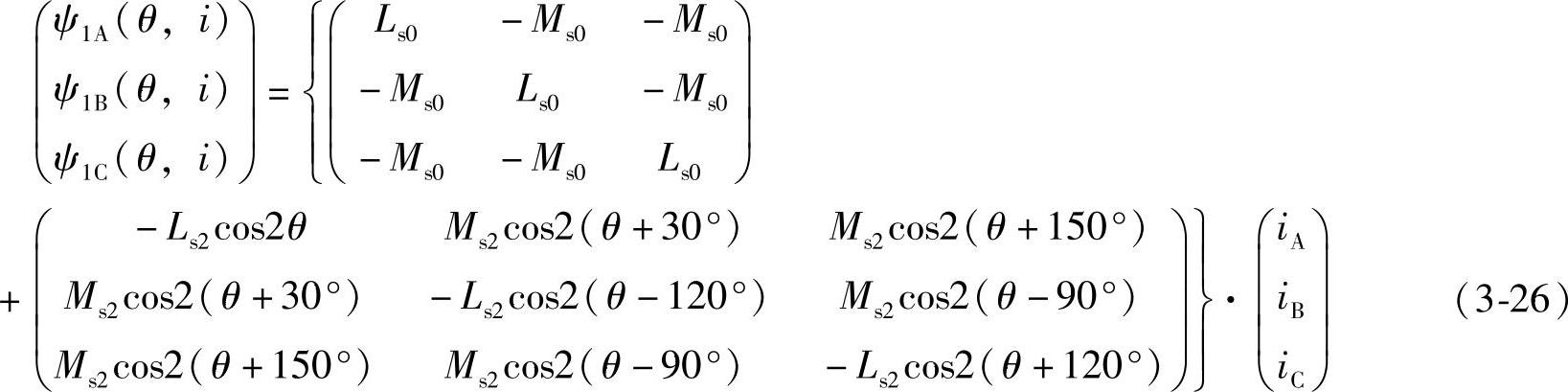
图3-4给出了PMSM各定子绕组的自感和互感与转子位置的关系示意图。

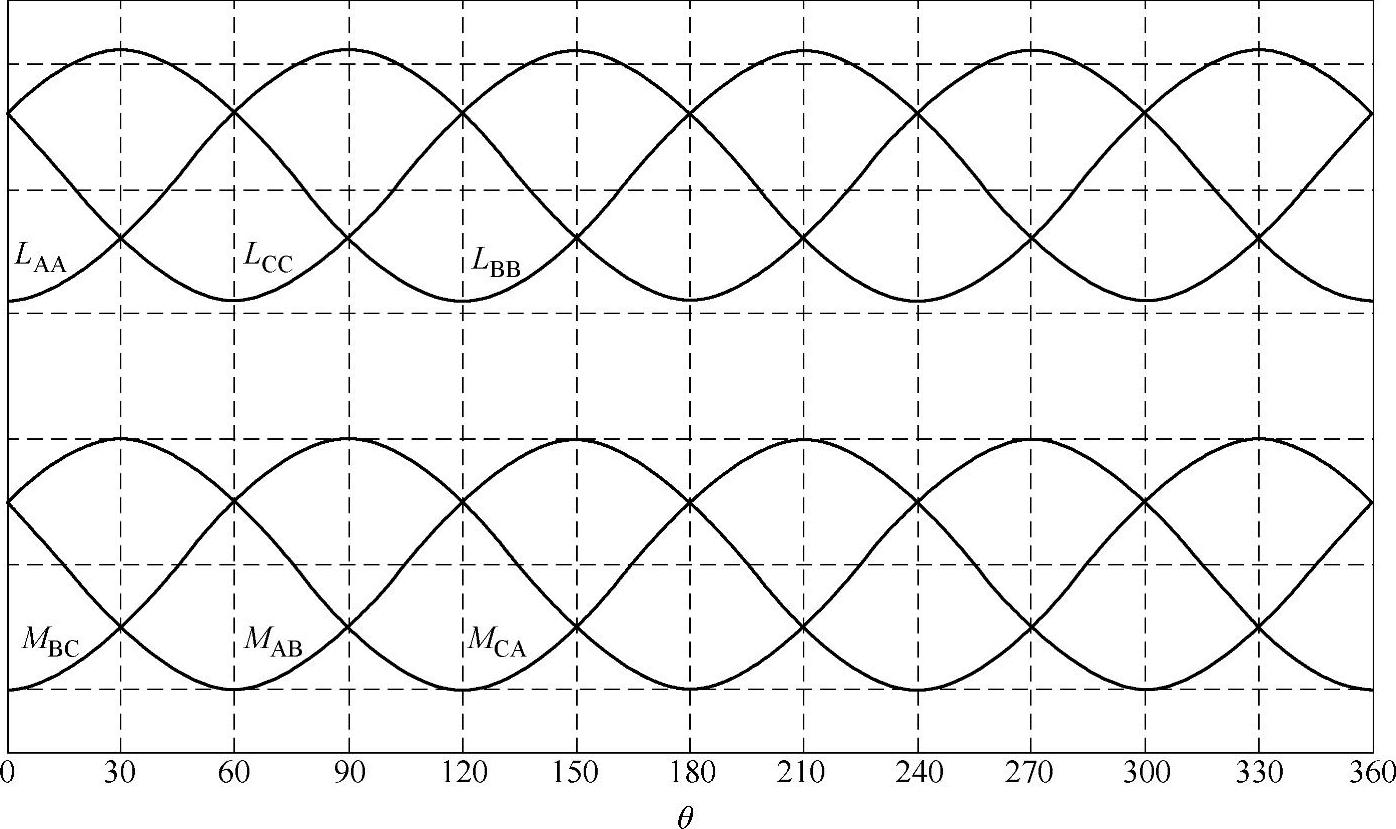
图3-4 PMSM定子绕组电感与转子位置关系示意图

3.定、转子绕组的互感计算

为了便于推导电动机的电磁转矩公式，我们将转子永磁体等效为具有电流i_f的转子励磁绕组f（对于正弦波磁场分布的PMSM来说，i_f是一个恒定值），仅在本部分推导转矩公式时使用。

转子绕组f与定子三相绕组之间的互感矩阵[M_sf]为

（M_fs）=（M_sf）^T （3-28）

需要指出的是，不管永磁体产生的是何种分布的气隙磁场，式3-3都可以用来表示永磁磁链，即下式成立

4.转子绕组的自感

虽然存在转子的凸极效应，但是这并不影响到转子励磁绕组自感L_ff，因为它不随转子位置而变化。这里引入L_ff也仅仅是为了推导电动机转矩的方便。