泵站的优化运行方法简介

泵站经济运行的程序设计是根据泵站的具体条件（泵站是否有水泵叶片调节机构或调速设备）和受益区的流量要求拟定泵站运行的程序框图，然后根据框图编写电算程序。有了好的运行方案才能设计出好的优化运行程序。优化运行程序和计算机及其相应的传感器和执行元件相结合，就可以使水泵机组按照预先设定的优化方案自动或半自动地实现优化运行。这里受本书篇幅限制，尚未写入电算程序设计部分的具体内容，而仅说明程序设计需要考虑的泵站优化运行方案。

在运筹学中，常见的优化方法有线性规划、非线性规划、整数规划和动态规划等。

（一）线性规划法

图9-18　泵站与灌区位置图

线性规划中，目标函数和所有约束方程（等式或不等式）必须是线性方程，即其中的决策变量的指数为1。例如，某河流上下游相距10km处已建成A、B两座灌溉泵站，灌溉甲、乙、丙三个灌区，如图9-18所示。各灌区所需供水量的下限分别为400万m3、800万m3和600万m3。A、B两座泵站最大供水能力分别为1200万m3、800万m3，每万m3水量的供水费用见表9-5所示。问A、B两座泵站对各灌区的供水量为多少时才能使供水费用最少。

表9-5　供水费用表　单位：元/万m3

为了解决上述问题，可以设泵站A对灌区甲、乙和丙的灌水量分别为：x1，x2，x3，泵站B对灌区甲、乙和丙的灌水量分别为：x4，x5，x6，上述问题可以用以下数学表达式来描述，在满足式（9-24）的条件下，使式（9-25）达到最小值。

以上各式中的x1～x6称为决策变量，又称未知变量，它们的任意一组定值，都代表一个具体的运行方案。式（9-24）中每个不等式均表示一个限制条件，称为约束条件。各决策变量均应满足非负数的条件。式（9-25）为目标函数，式中Z表示任意一种供水方案的供水费用，在所有的运行方案中，必须满足Z值最小或最大的要求（本例为求最小值，即最小化问题）。因为以上各式的决策变量均为一次方，即为线性方程，因此，以上问题可以用线性规划的方法来求解。计算方法有高斯法、单纯形法、二步法等，具体求解方法可参考运筹学或系统分析等有关资料。

上述线性规划问题可以归纳为两种类型：其一是在资源数量有限的情况下，寻求最有效利用的问题；其二是在任务一定的情况下，寻求完成任务而且资源耗费最小的问题。泵站还有很多类似问题都可以采用线性规划方法建立数学模型，列出约束条件和目标函数方程式并采用合适的计算方法求出各决策变量。

（二）非线性规划法

在求解一定约束条件下目标函数的极值问题时，如果约束条件或目标函数的方程式中有一个或多个非线性函数，则该类问题属于非线性规划问题。在泵站优化运行中，各种变量中存在大量的非线性函数关系，因此，非线性规划在泵站优化运行中的应用非常广泛。

现以多台全调节机组的泵站为例，以能耗最小为准则，确定最优的水泵叶片角度。设泵站安装4台28CJ56型轴流泵机组，每台机组轴功率不得超过1600kW，泵站的总流量不得小于50m3/s，需要确定的是在净扬程4m时各台水泵的叶片角度x1，x2，x3，x4为多少时才能使泵站总能耗最少。

为了解决上述问题，首先通过计算或现场测试绘制出如图9-14所示的水泵装置通用特性曲线图。然后确定水泵的装置效率与叶片角度之间，以及流量与叶片角度之间的关系式。由此可知，在4m净扬程下，装置效率和流量与叶片角度之间的关系式分别为：ηst=-0.027x2-0.539x+64；Q=-0.012x2+0.905x+22。根据不同角度的流量和装置效率，也可以确定在净扬程为4m时的机组功率与叶片角度之间的关系式为P=2.04x2+81.71x+1328.12。由此可以根据机组不得超载和泵站总流量等约束条件列出约束方程式9-26：

根据能耗最小的要求，可以列出目标函数方程式（9-27）：

由此可见，上述约束条件和目标函数方程均为非线性方程，因此求解上述问题的方法为非线性规划方法。其实，在泵站运行中，如按泵站效率最高，水费成本最低等都可以列出相应的约束条件和目标函数方程式。因此，非线性规划方法在泵站经济运行中的运用也是相当广泛的。

（三）动态规划法

动态规划法是一种解决多阶段决策过程的最优化为题的数学优化方法。首先将问题分为若干个阶段。每个阶段又有若干个状态。每个状态有其相应的状态变量，其中选择任意一种状态变量（即运行方案）就是一种决策。根据前一阶段最优决策和本阶段的决策，又可以有多种运行方案，也可以从中选择出最优方案。由此继续下去，这样直到最后阶段，就可以求出最优方案。因此，动态规划实际上就是多阶段决策的优化方法。例如，某泵站在一天24h的扬程Hsy是变化的，用动态规划法确定总耗电量最少的水泵叶片角度最优调节方案。现将一天分成3个阶段，每个阶段为8h。每个阶段的扬程Hsy分别为2m，4m，6m。设该站水泵型号为ZL30-7型全调节大型轴流泵，为了简化计算起见，假定水泵角度在-6°，0°，+6°三个角度变化。根据该泵性能、配套电机的效率曲线和流道阻力曲线，可以求出不同时段不同角度对应的流量、站效率、耗电量、提水量等参数，如表9-6所示。

表9-6　泵装置运行参数(www.xing528.com)

根据题意，可将3个阶段（n=3）和3叶片角度的运行方案组合绘成图9-19所示的网络图。在最末阶段（即时段）叶片角度只有3种可行状态C1，C2，C3（代表+6°、0°、-6°），用S3=｛C1，C2，C3｝。因此，最末阶段是无决策阶段。用上述3种角度运行的耗电量25054kW·h、20285kW·h、14897kW·h。

于是，n=3时

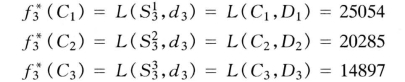
式中的“*”表示该阶段的最优决策。因此，阶段3的择优表达式为：

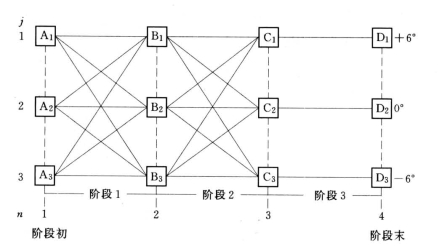
图9-19　水泵运行方案图

n=2时

故，阶段2的择优表达式为：

同样，在阶段1（即n=1）时，

由此可见，在阶段性1的中，总耗电量分别为43653kW·h，39881kW·h，36384kW·h。三个阶段的最优组合为A3-B3-C3-D3，即水泵叶片角度按（-6°）-（-6°）-（-6°）运行时，为耗电量最少。由上述各式可以归纳为以下择优表达式：

上式反映了动态规划递推关系的基本方程，故称为递推方程。

以上的优化过程实际上是无约束的动态规划方法。但在实际问题中，大量的是有约束的问题。例如，上述问题中，三阶段的最大提水量为344.1万m3，最小提水量为224.5万m3，如果要求提水量不得小于300.0万m3，则在计算时必须满足以下约束条件：

式中：gc为要求的总提水量（从阶段1到阶段N）；Qmax，k为第k阶段所提供的最大流量；α为松弛系数，可取为0≤α≤0.1。

上例仅为一个简单例子，实际工程可能更加复杂。如可供选择的水泵叶片角度不只是+6°，0°，-6°三个，而可能是+6°，+4°，+2°，0°，-2°，-4°，-6°，甚至更多。需要计算的运行时间不只是24h，而可能是更长的时间，可能划分的时段可能更多。这些将会使优化计算的工作量大大增加，但计算的基本原理和递推方程是相同的，如果能用计算机计算，也可以很快求得最优解。

另外，对于有约束的动态规划和前者的无约束问题的求解方法有所不同，在此不作详细介绍。

动态规划的优化方法在泵站经济运行中应用广泛，例如：对于多台泵的泵站，确定不同时段各台泵的叶片角度（或水泵转速）；对于同一水利枢纽中的多座泵站、水闸和调蓄容积（水库或湖泊等）的优化调度；对于多级泵站各台水泵的运行调度等都可以采用动态规划的方法进行计算，然后通过微机控制系统进行控制和调度。有些复杂的系统可以采用多层次多阶段的动态规划，具体计算方法另有专著介绍。