流速仪测流方法与稳流装置的选择与比测

流速仪测流法是用流速仪测得过流断面上的点流速，并根据点流速求断面平均流速，再乘以过流断面的面积，即得体积流量。

（一）一般要求

1.在测流时段内流速稳定

在水泵开机或工况变化（如阀门开度、叶片角度、水泵转速、进出水池的水位、电网频率或电压变化等）的过程中管道或渠道内的流量是变化的，流速也是变化的。另外，水面波动会引起水深和断面面积的测量误差。因此，在开机运行工况稳定后才能进行测试，同时，记录流速仪信号的连续测流时间不应少于2min，以便减小水流紊动或波动所引起的测量误差。

2.被测水流应满足水质和水温的要求

被测水流中的悬浮物（如柴草、泥沙等）或不溶解质含量的容许值的确定应以不影响测量精度为原则。水温不宜超过30°。

3.流速测量范围

被测水流的速度范围为0.2～5.0m/s。

4.流速仪的选用

流速仪有旋桨型和旋杯型两种。因旋杯型流速仪仅适用于比较小的流速，且易被杂草缠住，故在国际标准（ISO）中已明文规定，只能采用旋桨型流速仪测流。另外，要求流速仪的精度应满足要求，均方差σ≤1.0%。

5.流速仪的标定

流速仪工作一段时间后，由于轴承等机械磨损等原因，流速计算公式中系数将会发生变化。因此，流速仪需要在一定时段内重新进行标定。标定周期应按有关部门规定，根据清水或浑水等不同水质有所不同。当发现流速仪可能产生测量误差时，测试前要求对流速仪进行比测。比测应在专设的水槽中进行。如条件不允许，也可以在现场进行，但水流必须稳定（流速脉动小），比测位置宜在测流断面的中间区域，在同一测点上进行。比测所得的两台流速仪的流速差值不得超过流速仪本身均方差之代数和。符合要求的可以继续使用，否则应进行重新标定。

6.断面多点流速的同时性问题

对于较大的过水断面，一般需要测出多点流速后，再求出断面平均流速。然后用断面面积乘以平均流速求得流量。这时，可以用同时测量法（即用多台流速仪同时测出各点流速），也可以用不同时测量法（即用较少的流速仪在不同时间内测出断面各点的流速）。后者应该用参考流速仪修正各点流速。修正公式如下：

式中：vi0为修正后的任意点流速；vit为修正前t时刻的任意点流速；vr0为参考点在测量时段内的平均流速；vrt为参考点在t时刻的流速。

7.流速仪安装方向问题

流速仪轴线应与水流方向一致。这点在断面形状尺寸不变的直线管道和渠道测量时容易做到。但在大型泵站断面渐变进、出水流道测量时则难以满足要求。为了提高测量精度，要求在断面渐变进、出水流道测量流速时，流速仪轴线与水流方向的夹角应不超过5°。

（二）用流速仪测定明渠流量

1.用流速仪测定点流速

流速仪的旋桨，在水流推动下旋转，旋桨的转速n与水流流速v之间存在着一定的函数关系v=f（n）。每台流速仪通过在检定水槽中率定，给出在允许测速范围内的线性关系式（即检定公式）为：

式中：v为水流测点流速，m/s；n为流速仪旋桨转速，r/s，n=N/T，其中N为测速时段内旋桨的总转数，T为测速时段历时，s；k为流速仪的倍常数，m/r；C为流速仪的摩阻系数，m/s。

常数k和C值与旋桨的螺距及支承系统的摩阻力等因素有关，故每台流速仪的k和C值是不同的，要对每台流速仪进行单独检定，并通过回归计算，给出相应的检定公式。

用流速仪测定点流速，即把表示旋桨转数的电脉冲信号记录下来，代入式（3-17）即可。

流速仪的信号记录，在小型泵站中一般采用铃响或蜂鸣器，在大型泵站中则采用计数器自动记录。在记录时必须注意，要在水泵运行稳定后才能开始记录，记录历时不少于2min，并选取一段脉冲均匀出现的时段，作为计算转速的依据。

2.用流速仪测定明渠流量

用流速仪在明渠中测流，要求渠道是人工渠道，具有足够长度的平直规则断面，断面形状可以是矩形或梯形。如果不具备这样的条件，可以在原有渠道上加工一段长度为水面宽30倍左右的平直等截面人工渠道，如果是土渠也可以用砖或混凝土局部衬砌。

（1）测流断面的选择。测流断面应选在具有均匀流或渐变流的过流断面处，以保证过流断面为平面，在测流断面前后要分别具有大于水面宽度20倍和5倍的等截面平直段，以保证在测流断面附近不出现漩涡。

测流断面的形状要求是矩形或梯形，便于丈量。在测流前，要对测流断面进行检查，如果由于长期失修，断面附近长了青苔或残缺不全，必须清洗和整修；如果断面附近有淤泥等沉积或堆积物，也要清理干净以免影响测流断面附近的流速分布。

如果在测流断面附近流速分布不规则或水流不稳定，则可在离开测流断面3m以远的地方，加设稳流装置，如图3-13所示，以改善水流条件。稳流装置包括稳流栅、稳流筏、稳流板等，可根据需要选择其中的一种或两种。

图3-13　明渠中的稳流装置示意图

1—稳流栅；2—稳流筏；3—稳流板；4—流速仪支架；5—工作桥

（2）测线与测点的布置。测点数目应根据测流断面的尺寸来确定。当渠宽和水深大于或等于0.8m时，为了更好地控制流速分布，不应少于25个测点，分别布置在五根水平测线与五根垂直测线的交点上。如果断面尺寸较大时，则可按式（3-18）进行计算：

式中：A为测流断面面积，m2；n为测点总数。

当渠宽小于0.8m时，测线可减少为3根；当渠深小于0.8m时，每根测线上的测点可减少为3点、2点或1点。渠宽的限值，对于梯形渠道，应以渠底为准；梯形渠道的边坡较缓、边壁测线不能控制测流断面的横向流速分布时，可在边坡上增加测线。

测线是指几个测点连成的平行或垂直于水面的测速线，可根据渠道的宽度和水深选用。如果是宽浅型渠道，可以用垂直测线。如果是窄深型渠道，则可用水平测线。测线或测点的布置，均应根据流速分布来确定。一般在靠近明渠边壁、底部或水面附近，流速变化大，测线或测点应布置得密些，而在水流中部可布置得稀些，以控制两相邻测点间的流速差值不超过这两个流速中大者的20%为限。流速仪轴线至渠壁或底的距离，应控制在0.75d至200mm之间。流速仪轴线离水面应大于d，流速仪轴线间的距离应大于d+30mm，其中d为流速仪旋桨直径。

垂直测线的数目，根据断面的横向流速分布均匀程度而定，一般不少于5根。除两根靠渠壁的外，其他几根测线的位置则以能控制流速分布为原则。每根测线上的测点数目，按精度要求和水深，可采用多点法（即流速分布法）、五点法（水面附近、0.2H，0.6H，0.8H处及渠底附近）、三点法（0.2H，0.6H，0.8H处）、二点法（0.2H，0.8H处）及一点法（0.6H处），如图3-14所示。

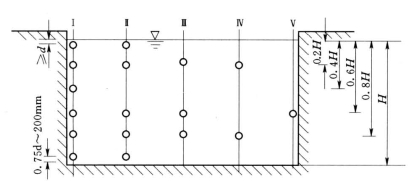
图3-14　明渠中测线与测点布置图

根据有关实测资料，五线三点法与五线五点法比较，偏差小于0.5%；五线一点法与五线五点法相比，偏差可控制在1%以内，泵站现场测试可推荐使用。而三线一点法的误差高达4%，这表明横向流速分布的规律性较差。因此用流速仪在渠道中测流，如果条件不允许或仪器不够，可适当减少测点而不宜减少测线。但目前有些泵站采用一线一点法（即测流断面中线0.6H处）测定流量，误差太大，不能作为泵站实测流量的依据。

（3）流速的测定。当测流断面确定后，应根据测线与测点的数目及位置设置流速仪支架。明渠中的流速仪支架一般有三种，如图3-15所示。当渠道的宽度和水深都比较小时，可采用水平移动的垂直测杆，在工作桥上定出测线的位置，如图3-15（a）所示。这种方法比较简单易行，但必须保证测杆上的流速仪方向一致，并与水流流向的偏角不超过5°；当断面水深比较大时，可采用水平测杆垂直移动，如图3-15（b）所示。这种装置需要测架和滑槽，以保证测点在同一过流断面上，并使断面垂直于水流方向。这种测架施测方便，便于人工操作。在大型渠道中，用移动支架难以保证精度，一般宜用固定支架，如图3-15（c），这种支架比较复杂，目前我国很少采用。

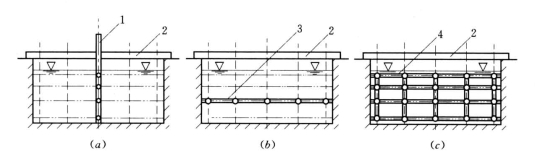
图3-15　渠道中的测速仪支架

（a）垂直测杆水平移动支架；（b）水平测杆垂直移动支架；（c）固定支架
1—竖杆支架；2—工作桥；3—横杆支架；4—固定支架；○—流速仪；虚线—垂直测线；二点画线—水平测线

在同一测流断面上，所有测点流速可不同时测量（图3-15a、b），也可同时测量（图3-15c）。不同时测量是将一排流速仪沿水平方向或沿垂直方向顺次施测，每次记录各台流速仪的信号，不少于2min。这种方法经常用在仪器不足，或避免阻塞影响过大的情况下，采用这种方法，必须保证整个测流时段内水流基本上是稳定的。为避免测流时段内因水流不稳定而产生的流速差异，应当在固定位置设置参考流速仪，并据此进行修正。在测流时段内要测出连续的参考点流速。如果参考点流速变化大，则说明测流时段内的流量不稳定，应该重测；如果参考点流速变化小，可按公式（3-16）修正任意点所测得的流速。

用流速仪在明渠中测流，由于流速仪在布置上受到限制，不可能直接测出边壁流速，只能借助于最靠近边壁的测点流速向外推算。在明渠中，常用的方法有两种：

1）由外推公式计算边壁流速。在国际标准（ISO）中推荐使用外推公式计算。

式中：vx为x处的流速，m/s；va为a处的流速，m/s；x为测点距边壁的距离，m；a为最靠近边壁的测点距边壁的距离，m；m为与雷诺数有关的指数，取值区间为4～10，一般取7。

（3-19）式是根据尼古拉兹在光滑管内对达到完全充分发展的紊流进行实验，整理出来的幂函数流速分布规律的经验公式。利用这个公式来外推边壁流速，就是假定边壁流速符合幂函数流速分布规律。由式（3-19）计算vx，将求得的一组x-vx值，点绘边壁流速曲线。

2）边壁流速系数法确定边壁流速。用边壁流速系数α乘以最靠近边壁的流速仪测量值va，即为边壁流速vx，vx=αva，边壁流速系数α，可根据边壁情况取值。斜坡边壁为0.83～0.91；陡峭粗糙边壁为0.85；陡峭光滑边壁为0.90。

这种方法简单方便，但由于边壁流速值在边壁上只有一个点，与流速曲线相连时，有一定的任意性。因此精确度比较低，一般在小型渠道中可以采用。

3.流量计算

在测点流速确定之后，计算测流断面的流量，可由下列步骤进行：①将同一测速垂线上的点流速值，按一定的比例点绘在测杆基线右侧相应的位置，在推算边壁流速的同时，用光滑曲线连接成流速分布图，如图3-16（b）所示。②用图解积分法^[5]计算各流速分布图上的曲线和基线所包围的面积，即为单宽流量qi。③在相应于测杆垂线的位置上，作单宽流量qi在渠宽上的分布图，并推算边壁流量值，如图3-16（c）所示。④用图解积分法计算qi分布曲线所包围的面积，即为断面流量。

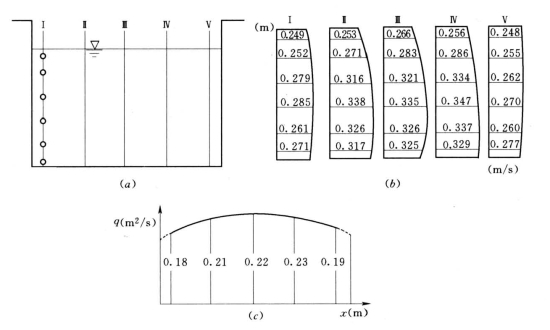
图3-16　用图解积分法计算明渠流量

在流量计算过程中要注意作图时所用的比例尺及相应的单位。

梯形断面的流量计算，可按虚拟矩形断面计算，虚拟的矩形断面，其宽度为水面宽，高度为水深。边壁流速曲线则以虚拟断面的边壁流速为零与单宽流量曲线连接，在梯形断面的那部分曲线，即为梯形断面的单宽流量曲线，量其所包围的面积，并乘以梯形断面面积，即为断面流量。

【例3-2】某排灌泵站安装12HBC2—40型水泵，采用流速仪法在明渠中测流。渠道断面为0.72m×1.15m的矩形。拟采用七台LS10型流速仪进行不同时测量。其中六台用于测流，一台用做参考流速仪。在测流断面上沿渠道宽度设置五根测线，对称均匀布置，每根测线上设六个测点，分别布置在水面附近0.2H，0.4H，0.6H，0.8H处及渠底附近；参考流速仪布置在测线Ⅲ的0.4H处。所测流速值如表3-1中第（3）、（4）栏所列。

表3-1　测点流速计算表

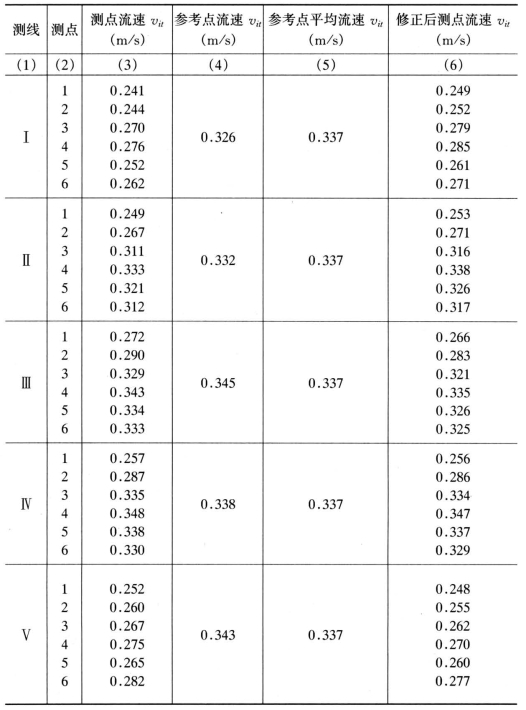
【解】1.用图解积分法计算单宽流量

用表3-1中的测点流速值绘制各测线的流速分布图［见图3-16（b）］，水深采用1∶20的比例，即1mm代表0.02m；流速采用的比例为1mm代表0.03m/s。并用图解积分法求单宽流量q，如表3-2所列。

表3-2　图解积分法求单宽流量

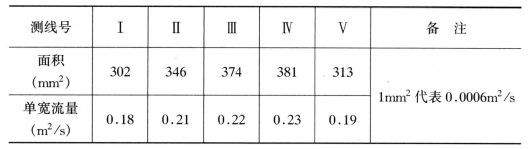
2.用图解积分法计算流量

用表3-2中的各测线单宽流量值，在测线相对应的位置上，绘制单宽流量分布图（见图3-15c），渠宽采用1∶20的比例，即1mm代表0.02m；单宽流量采用比例为1mm代表0.008 m2/s，再用图解积分法求其流量值。因面积为1484mm2，而1mm2代表0.00016m3/s，故流量Q=1484×0.00016=0.237m3/s。

3.绘制流速及单宽流量分布图

此时，渠道的边壁、水面、底部流速（或单宽流量），由于测点离边缘很近，采用了曲线光滑延长的方法。

4.误差分析

用流速仪测量渠道流量的精确度主要取决于水流流速分布的规律性、水流周期性的脉动、测速垂线、测点的数目及其分布、流速仪测速和断面丈量的工作状态、计算流量的方法及流速仪、量具本身的精度。测量误差分为随机误差和系统误差。

（1）随机误差。由于测流断面上的测速垂线为有限多，不能完全控制横向流速分布，必然会产生随机误差σm；误差值与每根垂线的断面宽度有关。参考ISO748，可采用相对均方差σm=0.5%。

在测量断面宽度时，存在着操作、读数等误差，误差具有随机性，可以根据多次同精度测量，用贝塞尔公式计算相对随机误差σb，见表3-3。

表3-3　渠道断面宽度测量值　单位：cm

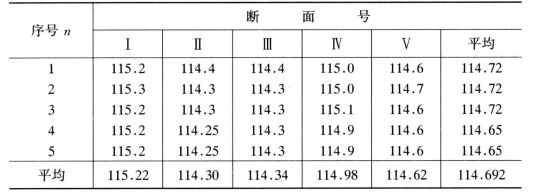
表3-4　渠道断面深度测量值　单位：cm(www.xing528.com)

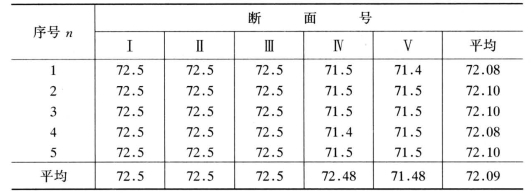
在测量断面水深时产生的随机误差，见表3-4。

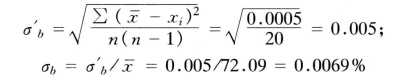
在垂线上的测点有限多，不能完全控制纵向流速分布，形成垂线上平均流速的随机误差，其数值与点数有关。本实验采用流速分布确定平均流速，则采用相对均方差σp=0.5%。

流速仪在测流过程中，由于水流的流态、测速与记录装置以及操作人员的熟练程度，都会产生随机误差σc，本试验采用相对随机误差σc=1.0%。

由于水流的波动、所测定的流速具有随机误差，其误差值随测量时间的增加而减小。本实验采用一条垂线上六个测点同时用示波仪记录2min，采用随机误差σe=0.5%。

所以，根据以上分析，按ISO5168及ISO748可用下式计算流量测量的随机误差σQ：

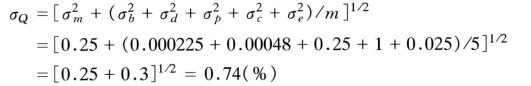
（2）系统误差。流速仪的标定误差：该误差已由厂家给出，LS10型流速仪的极限误差（δc）s=±3.0%。

断面测量误差：测量断面宽度和深度用的尺子，本身具有系统误差（δb）s和（δd）s，要求所采用的量具其系统误差不得大于1%，则（δb）s=±1.0%和（δd）s=±1.0%。故流量的系统误差（δQ）s可按下式计算：

（3）综合误差。流量的综合误差是系统误差和随机误差用方和根法合成：

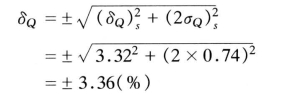
从流量的误差分析可以看出，影响测量精度的主要因素是流速仪的率定误差，国际标准（ISO）要求仪器的误差控制在±1%左右，如果流速仪的率定极限相对误差为±1.5%，则上例中的综合误差将下降到±2.54%。因此，为了进一步提高测试精度，要求尽量提高标定流速仪的精度或采用高精度的流速仪。

（三）用流速仪测定管道流量

1.大口径管道

（1）圆形管道直径应大于9倍的流速仪旋桨直径，矩形断面的短边应大于8倍的流速仪旋桨直径。

（2）测试断面的上游应有20倍管径长度的直管段，下游直管段长度应大于5倍管径。若管中发现有旋涡或流速分布不均匀，可在测流断面上游20倍管径处设置整流器。

（3）用流速仪测定半径为R的圆形压力管道中的流速时，测点数目n可由下式确定：

对圆形压力管道的测点布置，断面上总测点数不得少于13个点，至少有2根横穿测流断面的测杆，每根测杆半径上不少于3个测点。为了校核流速分布图形，在断面中心还应布置一个测点。一般测点总数不要超过37个。在断面测点数目相同的情况下，增加测杆数目比在测杆上增加测点的效果为好。在压力管中布置流速仪时，必须保证流速仪轴线与管壁间的最小距离为0.75d，流速仪轴线间距不小于d+30mm，其中d为旋桨直径。

（4）圆形管道中测点布置的方法有多种，现仅介绍圆环等面积法和圆环等流量法。

1）圆环等面积法。圆环等面积法的测点布置是按各圆环面积相等的原则进行的，即将管截面分成若干个同心圆环，使各圆环（最外侧圆环和内圆除外）的截面积相等。测点就在这些圆环的中心圆周线与通过圆心的直径测杆的交点上，各测点的位置可由下式确定：

式中：ri为半径测杆上第i个测点距圆心的距离，m；R为圆管的半径，m；i为半径测杆上测点序号（自圆心向管壁）；n为每根半径测杆上测点的数目（不括圆心处的测点）。

2）圆环等流量法。圆环等流量法是基于使测点所代表的各圆环的流量大致相等的原则来确定测点位置的，测点的布置规律由下式确定：

式中：rn=R-0.75d（d为流速仪旋桨直径）；其余符号同式（3-21）。

四根半径测杆的测点布置形式如图3-17所示。但应注意：两种方法各测点相应的ri含义是不同的。当n=3～8时，由式（3-22）计算测点位置。

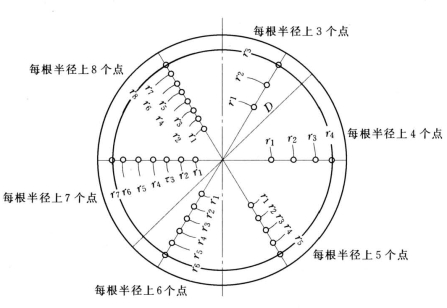
图3-17　圆形管道测点布置

（5）流量计算。计算流量的方法，与测点布置方案有关，圆环等面积或圆环等流量布置测点可用图解积分法确定流量。即设v为极坐标系r和θ上的某点流速，R是测流断面平均半径，则由二重积分可得断面流量Q，即

若v沿圆周不变，则上式为：

用图解积分法求解这个积分式有以下三种形式：

1）绘制各测杆的流速分布曲线，如图3-18（a）中r轴上方所示。将流速vi与所对应的半径ri的乘积viri标在r轴下方，并计算r-vr曲线所包围的面积，以一定的比例尺和2π乘该面积值，即得式（3-24）所表示的流量值。

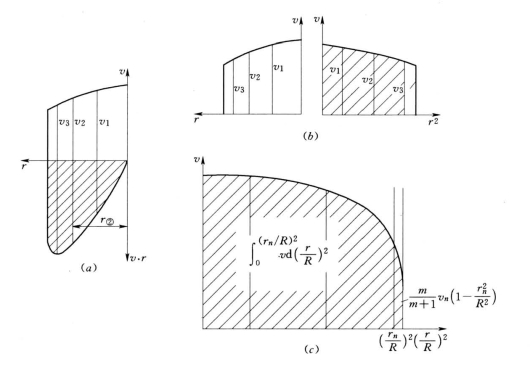
图3-18　由图解积分法计算圆管流速

2）由公式（3-25）通过定积分变换，可得另一种积分表达式：

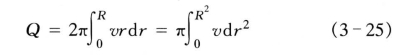
绘制以r2为横坐标的流速分布曲线，如图2-18（b）所示，求出图中阴影部分的面积，乘上相应的比例尺、π值即得流量Q。

3）由公式（3-25）经定积分变换，还可得另一种积分表达式：

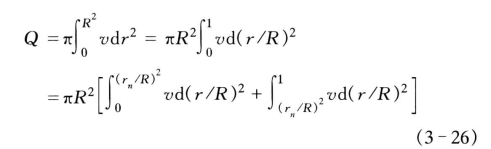
绘制以（r/R）2为横坐标的流速分布曲线，如图3-18（c）所示，求出图中阴影部分的面积，乘上相应的比例尺和圆面积，即得流量Q。

上述方法，均可用来确定圆管中的流量。应用时可根据具体情况任意选择，或用几种方法比较，用任意两种方法所计算的流量值，其偏差应不超过平均值的1%。若测量精度要求较高，则应将每根测杆上的测点流速都用图解积分法计算出流量后，再取平均值。如果测量精度要求不很高，则可取各测杆上测点流速的平均值，再用图解积分法计算流量。

【例3-3】某泵站压力管道的直径为1.2m，用13台LS10旋桨型流速仪测速，按圆环等面积法布置测点。测得四条半径上的流速如表3-5第（3）栏，试计算其流量值。

【解】（1）已知压力管道半径R=600mm。根据式（3-21），每根半径上的测点数为n=3。按圆环等面积法布置测点，则分别将i=1、2、3代入式（3-22），得r1=244.9mm；r2=424.3mm；r3=547.7mm，但因安装中有误差，实际量得各测点的r值，如表3-5中第（4）栏所列。

（2）计算vr及r2的值，列入表中第（5）、（7）栏；并绘出r-vr及r2-v关系曲线。

（3）用外推公式绘出边界流速曲线。

（4）计算出各图形的面积，即为各半径上的流量Q'及Q"，列入表3-5中的第（6）、（8）栏。

（5）将各半径测杆计算得的Q'，或Q"取算术平均值。

Q'=（1.066+1.068+1.067+1.065）/4=1.0665（m3/s）；Q'=（1.063+1.061+1.061+1.059）/4=1.061（m3/s）Q'与Q"的差值小于1%，则其断面流量取其平均值为：Q=（Q'+Q"）/2=（1.0665+1.061）/2=1.064（m3/s）。

表3-5　圆管图解积分法流量计算表

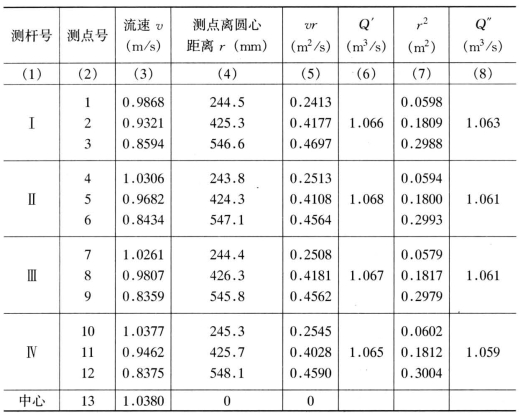
注　表中的中心点（13号）流速，只作流速图形的校核用，不作流量计算的依据。

（6）误差分析：在压力管道中，用流速仪测流的误差源，与使用的仪器、测试的方法、计算公式以及人为的因素等都有关系。针对本例中所采用的流速仪测流的误差源作如下分析：

1）系统误差：①流速仪本身的误差。按照检定公式所给出的均方σ≤1.5%进行计算，这里采用极限相对误差为±3.0%；②流速仪安装按照ISO3354的规定，流速仪的旋桨轴应与水流流速方向相平行，最大偏角不得超过5°。在该情况下，其极限相对误差为±0.5%；③流速仪的安装位置不可能完全固定在要求的点上，其极限相对误差参照ISO取值为±0.1%；④由于流速仪灵敏度限制，当水流存在高频波动或紊动时，流速仪的有限反应来不及改变转速而引起示波器记录流速的极限相对误差估计为±1%；⑤测杆对断面的堵塞所引起的流速误差：经计算，测流杆前缘断面面积（圆杆直径与长度之积）占管道断面积的2.5%。由此项引起的流速相对极限误差为±［（2/3）×0.125×2.5%］=±0.21%；⑥测点数不足而引起的极限相对误差，参照ISO取值为±0.1%。

2）随机误差：①流速仪转速n的计数和计时误差。本次测量记录持续时间为120s，时差估计值为0.2s，再加上测量时间的不足引起的误差为0.1%，故误差为：（0.2/120+0.1）%=0.27%；②流速缓慢波动所产生的误差。在测量时间较短的情况下来不及修正在流速中缓慢波动的积分误差，参照ISO定为0.1%；③图解积分作图的误差，它的大小可由曲线v=f（r2/R2）总图形面积的百分数来表示。根据作图情况取值为±1.0%；④计算流量曲线所包围的面积可能产生的误差。其大小取决于作图的比例尺。比例越大，精度越高。计算规定二次（或两人）数格差值控制在±1%以内；⑤图解确定系数m值产生的误差。由决定边壁流速，其中m值是由距管壁较近的曲线斜率来确定。参照ISO取为±0.05%；⑥断面测量的误差。10次量得测流断面平均直径的相对均方差为0.2%；量具用千分尺，其刻度误差为±0.1%，作为系统极限误差考虑。

3）误差估算。总误差可用方和根法合成，即：

其中系统误差项，由于各单项的误差符号不能完全确定，应作未定系统误差看待，因此亦采用方和根方法合成；随机误差的合成，在95%置信度情况下，各误差项又相互独立（不相关），则其总的极限误差为：

根据前述，流量测量误差为：

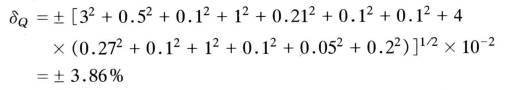
2.小口径管道

（1）管径小于或等于500mm，大于或等于250mm时，可用CBL—1型泵站流速仪测定流量。如图3-19所示。

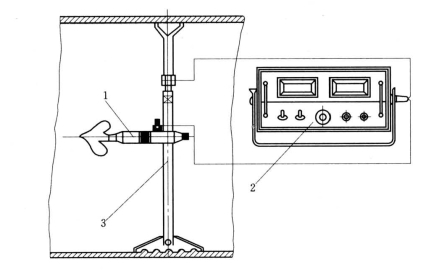
图3-19　泵站流速仪测速装置

1—流速仪；2—计数器；3—支架

（2）当测流断面选择在上游具有长度为15倍管径的直管段，下游具有长度为2倍管径的直管段时，可用一点法测流。即管道中心流速vc，乘以流速系数kp及断面面积A，则求得流量Q为：

流速系数kp与管道直径及测流断面上游直管段长度有关。当直管段长度大于或等于15倍管径时，可取kp=0.88。在良好的测量条件下，置信度为95%的极限误差可控制在±3%。

（3）测流断面上游直管段长度小于15倍管径，而大于10倍；或当直管段长度大于或等于15倍管径，而下游直管段长度小于2倍管径时，可采用三点法测流。在具有良好测量技术的条件下，置信度为95%的极限误差可控制在±3%。

三点法测流是在管直径的两端距管壁0.125D处分别设两个点，加上圆心共三个点，三个点的流量计算公式为：

式中：v2及v'2分别为距管壁0.125D处的流速。