Hy-Vo齿形链中心距变动量的计算方法优化

已知：链轮齿数z₁=z₂=35，模数m₁=3.0319mm，链轮压力角α₁=30°，量柱测量距M_R=105.881mm，量柱直径d_R=6.0mm，Hy-Vo齿形链基本节距p=9.525mm，链条节数L_p=84。4.11.1.1模型简化假设

1）在张紧测量力的作用下，链条上下两边都为紧边，该假设与实验条件相吻合。

2）滚销之间始终保持纯滚动。

3）暂不考虑节距公差对中心距变动量的影响。

由以上几个假设可以推出，对于奇数齿，当一个链轮轮齿朝上时，另一个链轮必然轮齿朝下。如果不满足这个相位关系，如两个链轮轮齿同时朝上，由已知条件可以看出，a边包含25个链板长，而b边则包含24个链板长，这与假设1矛盾。

4.11.1.2外啮合Hy-Vo齿形链中心距变动量的数学模型

为了使模型简单，应先选择一个适当的初始位置。经过分析，选择其中一个轮齿朝上，另一个轮齿朝下为初始位置建立模型，这样可简化模型的建立过程。由图4-37可以看出，销轴1和链板2始终存在间隙，这样就有可能避免啮入链板在初始啮合的过程中，出现链板上翘和滞后啮合。

1.外啮合的啮入状态

为验证外啮合Hy-Vo齿形链能否避免链板上翘，可以追踪啮入链板的运动轨迹。在图4-38中，链板的结构可以保证链板1、链板2、链板3全部处于水平位置。

图4-37 初始状态下各个坐标系的建立

1—销轴 2—链板

图4-38 外啮合Hy-Vo齿形链啮合状态

首先让链轮转动π/z，在链条张紧力的作用下，若无结构限制，链板1、2将始终保持水平，链板3则随链轮一起转动，运动状态轨迹如图4-39所示。由图可见这种外啮合Hy-Vo齿形链完全可以避免链板上翘。因而可以认为图4-37中轮齿朝上时与该轮齿啮合的链板a已经完全啮合就位并处于水平位置，b链板在运动到a链板现在所处位置之前始终保持水平。

2.外啮合的坐标变换关系

如图4-37所示，以该位置为初始位置建立坐标系。其中XOY是定坐标系，即以链轮中心为坐标原点，OX始终沿两个链轮中心线连线方向；O_a、O_b分别是圆弧C_a、C_b的圆心，x_aO_ay_a固连在链板a上，O_ax_a在O_aO_b的连线上，x_bO_by_b固连在链板b上，O_bx_b在O_aO_b的连线上。图4-37的坐标变换关系如图4-40所示。

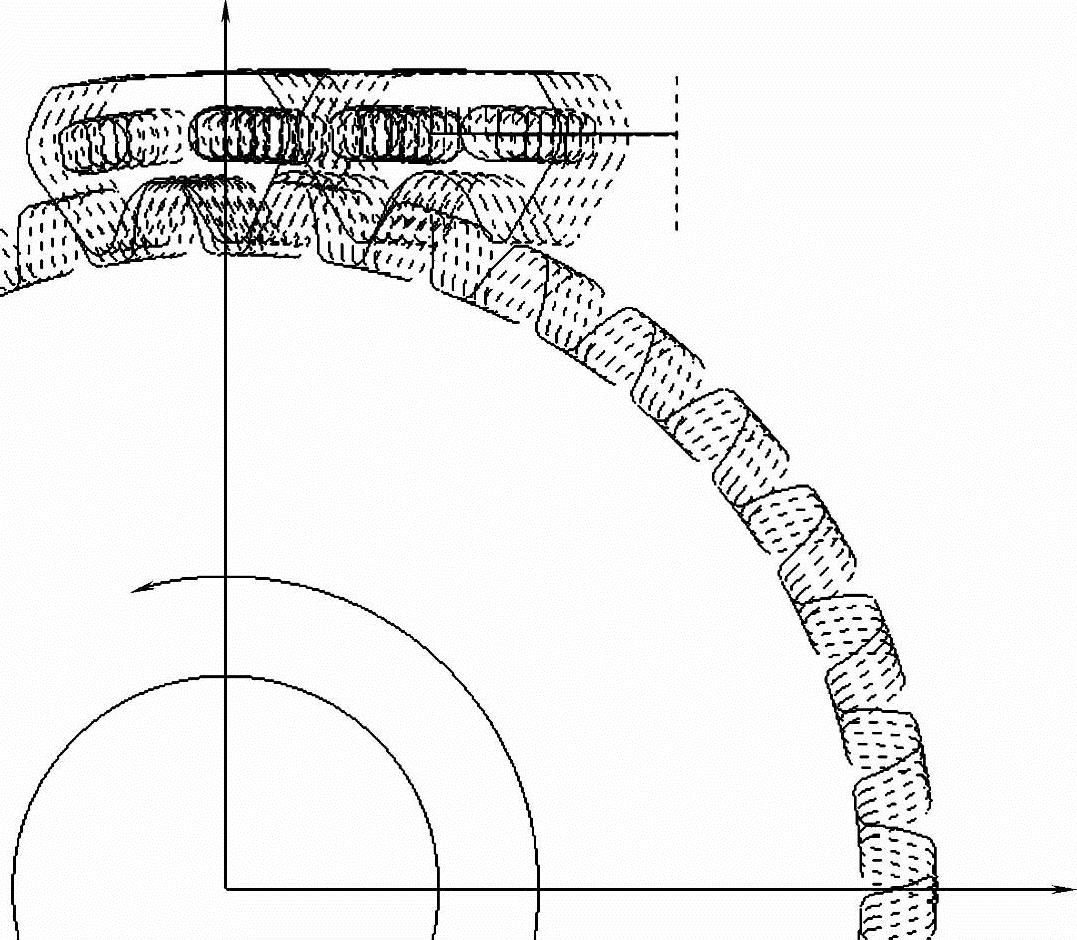
图4-39 外啮合Hy-Vo齿形链运动状态轨迹

图4-40 啮合点的运动过程

1）x_aO_ay_a→XOY的坐标变换过程如下。如图4-41所示，x_aO_ay_a→X′O′Y′的坐标变换如下：

其变换矩阵为MOa，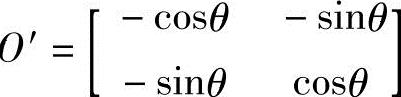

图4-41 x_aO_ay_a→XOY的坐标变换

则

X′O′Y′→XOY的坐标变换如下：

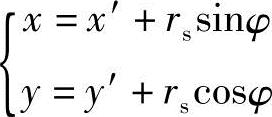
其变换矩阵为，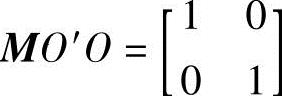

则

综合式（4-26）、式（4-27）两式，得X_aO_aY_a→XOY的变换矩阵为

2）x_bO_by_b→x_aO_ay_a的坐标变换过程如下。如图4-42所示，x_bO_by_b→x₁O₁y₁的坐标变换如下：

其变换矩阵为，则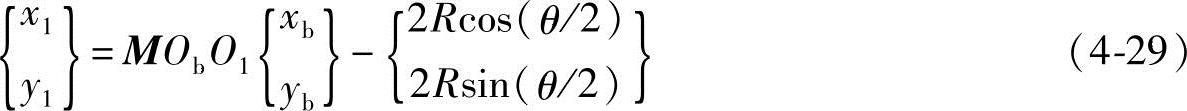

3）x₁O₁y₁→x_aO_ay_a的坐标变换如下：

图4-42 x_bO_by_b→x_aO_ay_a的坐标变换

其变换矩阵为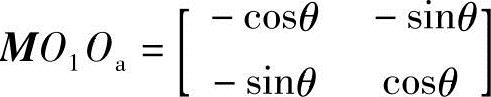

则

综合式（4-29）、式（4-30）两式，得x_bO_by_b→x_aO_ay_a的变换矩阵为

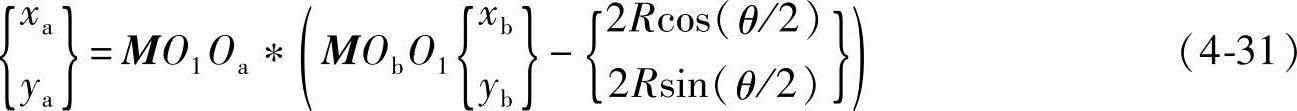
4）x_bO_by_b→XOY的坐标变换。综合式（4-28）、式（4-31）两式，得x_bO_by_b→XOY的坐标变换为(www.xing528.com)

4.11.1.3外啮合Hy-Vo齿形链中心距变动量的计算

首先考虑链轮从初始位置旋转π/z的过程中啮合点的轨迹图。其程序框图如图4-43所示。

用MATLB编程如下：

图4-43 程序框图

程序运行结果，即啮合点轨迹图如图4-44所示。外啮合Hy-Vo齿形链中心距波动量的建模图如图4-45所示。

图4-44 啮合点轨迹图

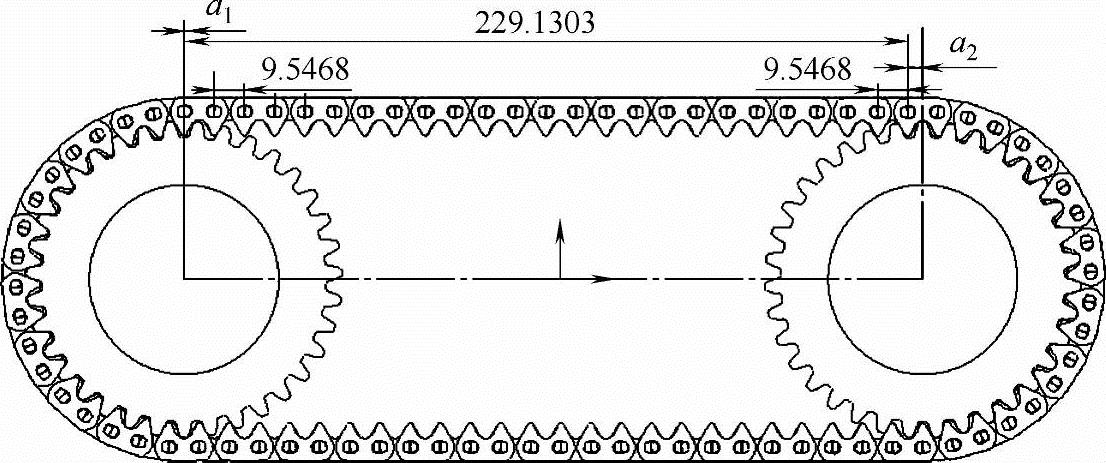
图4-45 外啮合Hy-Vo齿形链中心距波动量建模图

由图4-44啮合点轨迹图很容易通过编程求得d=a₁+a₂的波动图，用MATLB编程如下：

程序运行结果，即d值波动图如图4-46所示。可以算得，沿X方向的最大波动量：x_max=d_max-d_min=（4.7122-4.6969）mm=0.0153mm。

同样可得y方向的波动，程序如下：

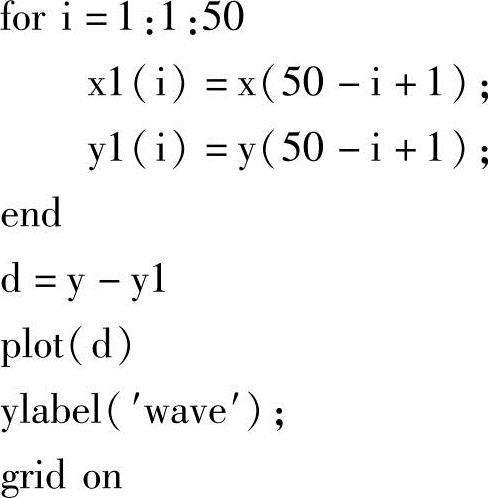
图4-46 d值波动图

程序运行结果，即y轴的波动图如图4-47所示。

当波动量取最大值y_max=0.5338mm时，该波动量引起的中心距变动量为：，远小于X方向的最大波动量0.0153mm，因此，可以忽略Y方向的波动量对中心距变动量的影响。由轮换对称性知，链轮转动一周时其中心距的最大变动量为0.0153mm。

图4-47 y轴波动图

4.11.1.4内-外复合啮合Hy-Vo齿形链中心距变动量的分析与估算

由于内外复合啮合Hy-Vo齿形链的啮合情况过于复杂，啮合过程中有销轴对滚珠、链板外侧与内侧的交替啮合，同时伴随链轮与链板之间的相对滑动，其数学模型的建立十分复杂，甚至是不可行的。但啮合过程中可能存在链板上翘甚至卡节等不可回避的问题。综合考虑以上因素，采取定性与定量结合的轨迹追踪法来探讨此问题。

如图4-48a所示，若在此位置保持链板3处于水平，由于结构限制，链板1将下倾11.9°。实际上，在链条张力F的作用下，链板1应处于水平状态。可见，图4-48a的状态在实际啮合过程中是不会出现的，且链板3一定存在上翘角。如图4-48b所示，保持链板1处于水平位置，则链板3将存在2.5°的上翘角。

图4-48 内-外复合啮合Hy-Vo齿形链的上翘角

a）保持链板3处于水平 b）保持链板1处于水平

设链板1、2之间的夹角为α，链板2、3之间的夹角为β，链板3的上翘角为γ，链板1中心位置与两个链轮中心连线的距离为h，与y轴的距离为s，以图4-48b为初始位置，逆时针转动链轮π/z，均匀追踪六个位置状态，如图4-49所示。可见，内外复合啮合Hy-Vo齿形链在啮入过程中，存在链板上翘现象，但不存在卡节现象。六个位置状态追踪结果见表4-1。

表4-1 六个位置状态追踪结果

图4-49 内-外复合啮合Hy-Vo齿形链运动轨迹图

由α值可以看出，链板2离开状态1后就开始上翘，并且上翘角逐渐增加。由β值可以看出，由于链板上翘角的影响，链板2、3之间的夹角并不是均匀变化的。由γ值可以看出，链板3的上翘角逐渐均匀减小，但在链轮转过π/z，仍然不能完全啮合就位。由h值可以看出，链条紧边中心线仍然存在小量的上下波动。

在表4-1中，s值对中心距的影响最大。若不存在链板上翘，在状态1，s应恰好对应2p。在状态2，s应恰好对应（2-1/5）p。每个状态依次减小1/5p。算出每个状态对应的伸长量见表4-2。

表4-2 各状态对应的中心距伸长量

考虑到传动是一对链轮，当其中一个链轮处于状态1时，另一个链轮必然处于状态6。因而，以上单个链轮的六个状态相当于一对链轮的三个状态。相应的中心距伸长量见表4_-3。

表4-3 实际中心距伸长量

链轮转动一周时，中心距变动量为最大伸长量与最小伸长量之差：ζ=0.0815-0.0625=0.019mm。