对于上面列举的两种计算方法可以用下述的实例来做进一步的分析对比。
例3-1 已知一链传动,节距p=50.8mm;齿数z1=6,z2=60;暂定中心距a0p=12。根据这些参数求得的链长节数X经圆整后取为64节。则按上述各种中心距的计算方法得到的a值分别列出,并汇总于表3-9。
表3-9 例3-1的中心距a计算值(单位:mm)

(1)按渐开线函数法计算中心距a
由于i≠1,根据表3-7利用插值法计算得到:f4=0.19950
那么,a=f4p[2X-(z1+z2)]=0.19950×50.8×[2×64-(6+60)]mm=628.3mm
(2)按Winklhofer法计算中心距αmin和αmax按图3-9a计算,已知: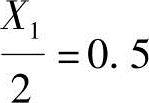 ;
;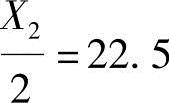 ;
;
 (https://www.xing528.com)
(https://www.xing528.com)
按图3-9b计算,已知: ;
;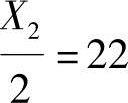 ;
;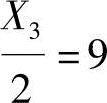


例3-2 已知一链传动,节距p=50.8mm;齿数z1=20,z2=60;暂定中心距a0p=40。根据这些参数求得的链长节数X经圆整后取为116节。则按上述各种中心距的计算方法得到的a值分别列出(计算步骤参见例3-1),并汇总于表3-10。
表3-10 例3-2的中心距a计算值(单位:mm)

由上述两个例子进行分析对比可知:两种计算方法即使在极端传动参数条件下一致性也很好。
应该指出,由图3-9可得到一个重要的概念,即当一条链条围在两个链轮上并且双边绷直时,在不同的链轮转角位置下,其中心距a是变动的,变动量Δa=amax-amin。对于普通的滚子链传动来说,一般由于链轮齿数z不会取的很少,中心距的变动还不太成问题。但是对于长节距的滚子输送链来说,却必须对此加以注意。这是因为滚子输送链的各链边是被约束在轨道上移动的,而且链轮直径不希望设计得很大,因而齿数取得较少,这样中心距的变化量就显得相当大。应当用弹簧等装置随动张紧。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




