中心距计算方法一：渐开线函数法

由图3-8可得链长的计算公式如下：

L=2[r₁θ+（r₂-r₁）tanθ+r₂（π-θ）]

=2[（r₂-r₁）（tanθ-θ）+πr₂]

=2[（r₂-r₁）invθ+πr₂]

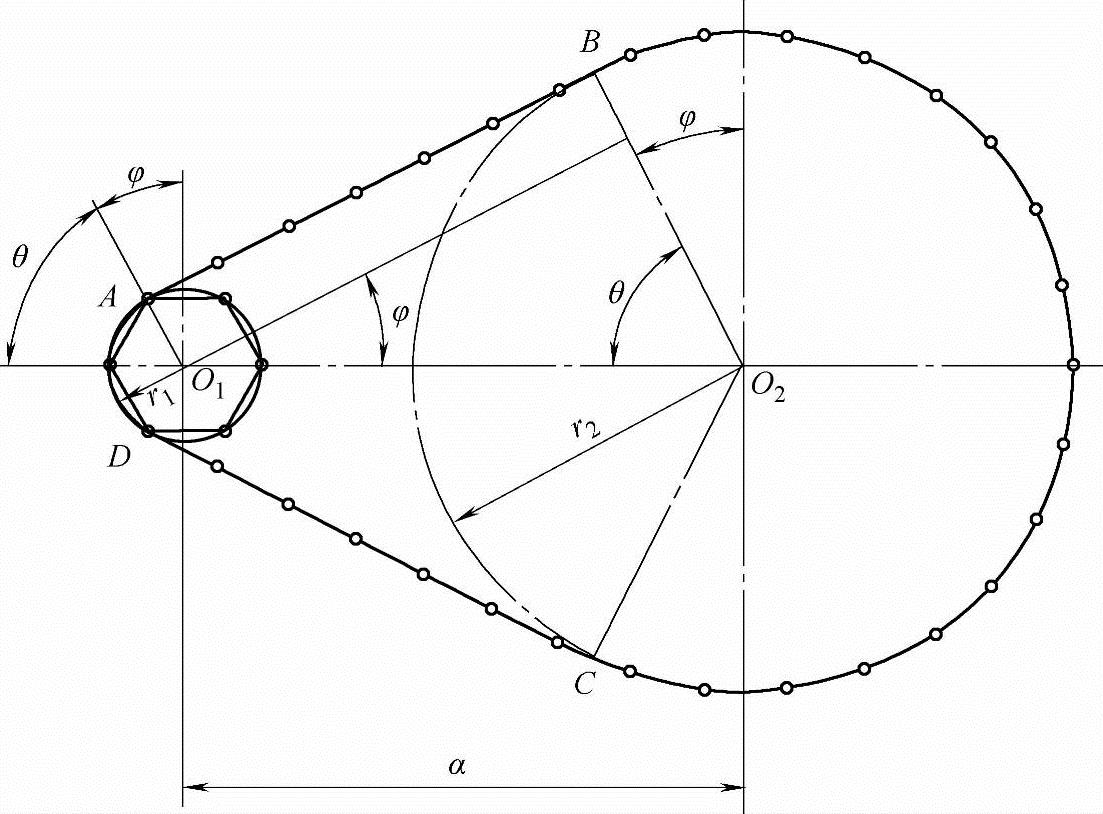
图3-8 链传动简图

由上式可求出θ为

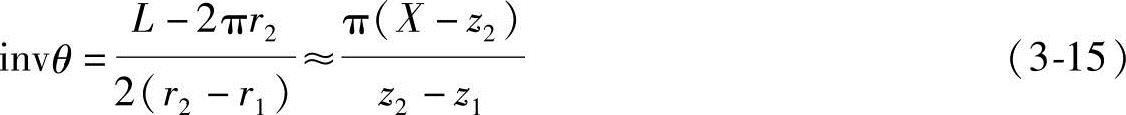
中心距a为

为了方便计算，将式（3-16）转化如下：

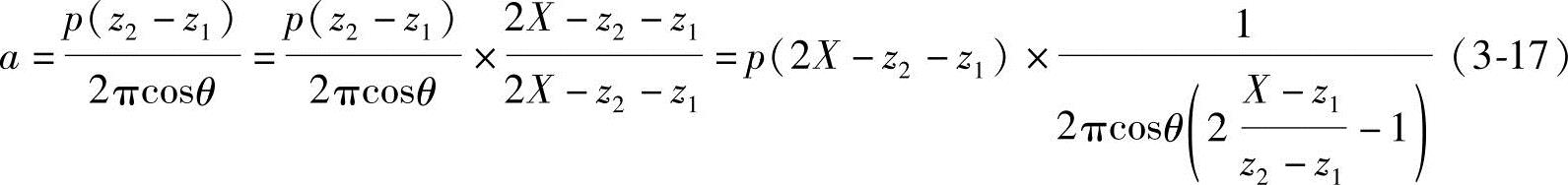(www.xing528.com)

设

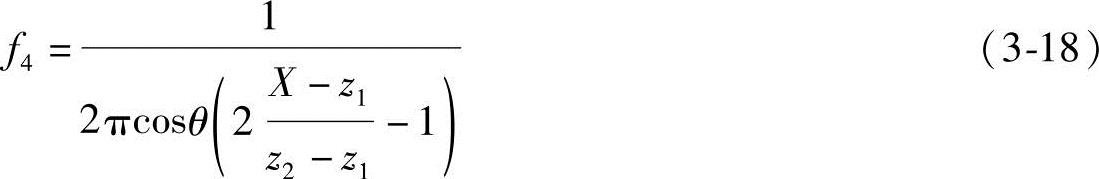
那么，式（3-17）可简写为式（3-8）：

a=p（2X-z₂-z₁）f₄=f₄p[2X-（z₁+z₂）]角θ由式（3-15）求出，即

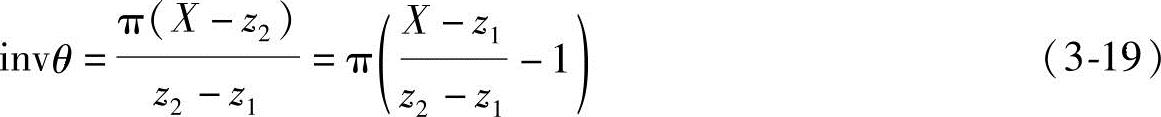
式中：L为链长（mm）；X为以节数表示的链长，即链长节数；a₀为按结构考虑暂定的中心距（mm）；a为链长圆整后重新计算的中心距（mm）；a_0p为以节数表示的暂定中心距；a_p为链长圆整后，以节数表示的重新计算的中心距；p为链条节距（mm）；r₂和r₁为大小链轮的分度圆直径（mm）；z₂和z₁为大小链轮的齿数。

由式（3-8）、式（3-18）、式（3-19）可知，只要给定一个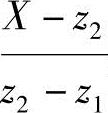的值，就可得到相应的f₄值。因此，可制定出如表3-7所示的系数f₄数值表。为了提高计算精度，当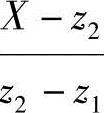的值位于表列两值之间时，f₄值应用插值法求取。

当传动比i=1时，即z=z₁=z₂，分式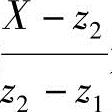无意义，此时就不必利用式（3-8）、式（3-18）、式（3-19）来计算，而应改用由图3-8所示的几何关系所推得的式（3-7）来计算中心距，即

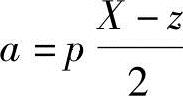
实践表明，用渐开线函数法计算链传动的中心距，其计算结果具有足够高的精度。