【知识目标】
1)理解纯电阻、纯电感、纯电容电路的概念。
2)掌握它们的电压、电流、功率的关系。
【技能目标】
1)学会函数信号发生器、示波器、毫伏表的使用方法。
2)掌握用示波器观测正弦交流电压的幅值与周期,并能正确读数。
3)掌握用毫伏表测量交流信号的有效值的操作方法。
【情感目标】
激发学生对信号测量器材的认识,提高动手能力。
正弦电路不同于直流电路,在交流电路中不仅要考虑耗能元件——电阻,而且要考虑储能元件——电感和电容的作用。
一、电阻元件的交流电路
观察与思考
问题:什么电路是纯电阻电路?
只含有电阻元件的交流电路叫做纯电阻电路。如含有白炽灯、电炉、电烙铁等的电路(如图4-21所示)。
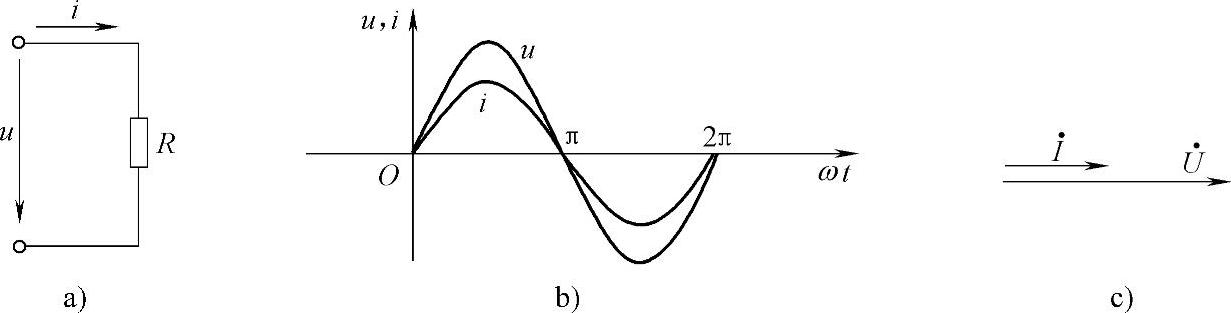
图4-21 纯电阻电路
1.电压电流关系
1)瞬时关系: u=iR (4-19)
2)相量关系: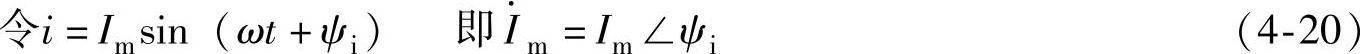
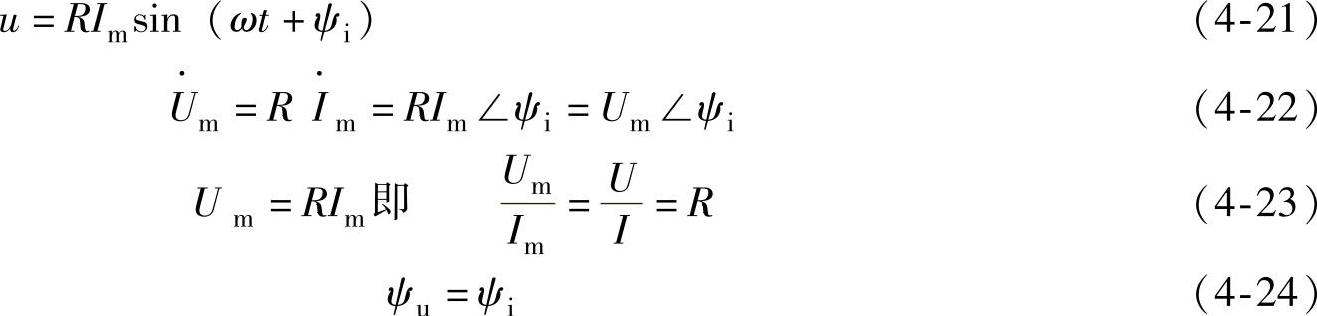
u、i波形与相量如图4-3-1b、c所示。
2.功率
1)瞬时功率p=ui=UmImsin2ωt=UI(1-cos2ωt) (4-25)
2)平均功率 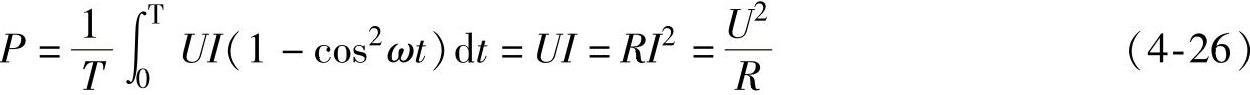
在电阻元件的交流电路中,电流和电压是同相的;电压的幅值(或有效值)与电流的幅值(或有效值)的比值,就是电阻R。
练一练
【例4.8】 已知某白炽灯的额定参数为220V/100W,其两端所加电压为U=2202sin(314t)V
试求:(1)交流电的频率。
(2)白炽灯的工作电阻。
(3)白炽灯的有功功率。
解:
(1)交流电的频率: 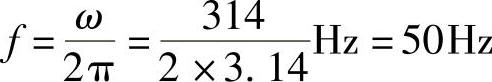
(2)白炽灯的工作电阻: 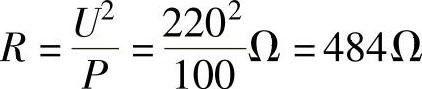
(3)白炽灯的有功功率: 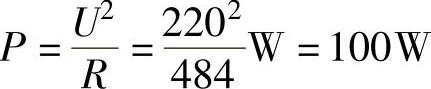
【例4.9】 将一个阻值为484Ω的白炽灯,接在u=2202sin(314t-60°)V的交流电源上,
试求:(1)通过白炽灯的电流为多少?写出电流的解析式。
(2)白炽灯消耗的功率是多少?
解:
(1)电压的有效值: 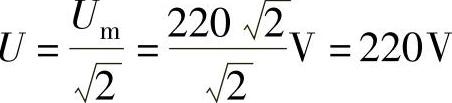
电流的有效值: 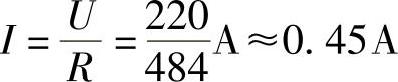
电流的解析式: 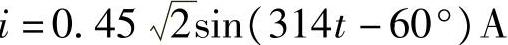
(2)白炽灯消耗的功率: P=UI=220×0.45W=99W
二、电感元件的交流电路
如图4-22和图4-23所示的两个电路图的实验效果为什么不同呢?
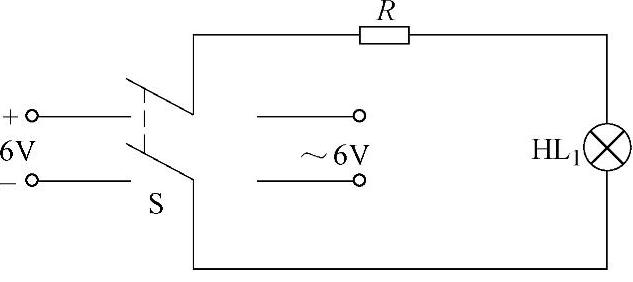
图4-22 电阻电路
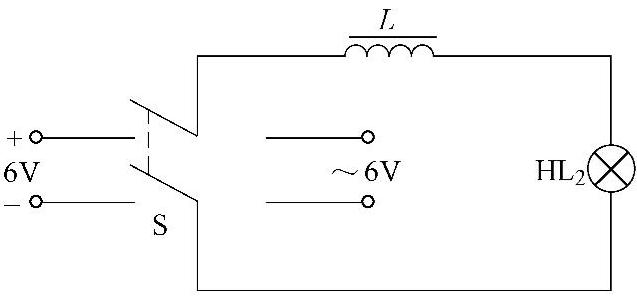
图4-23 电感电路
 接6V直流电源:白炽灯HL1和HL2亮度相同。
接6V直流电源:白炽灯HL1和HL2亮度相同。
 接6V交流电源:白炽灯HL2明显变暗。
接6V交流电源:白炽灯HL2明显变暗。
 电感线圈对直流电和交流电的阻碍作用是不同的。
电感线圈对直流电和交流电的阻碍作用是不同的。
1.电压电流关系
1)瞬时关系:

2)相量关系:令i=Imsin(ωt+ψi)即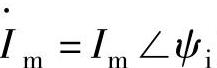 如图4-24c所示。
如图4-24c所示。
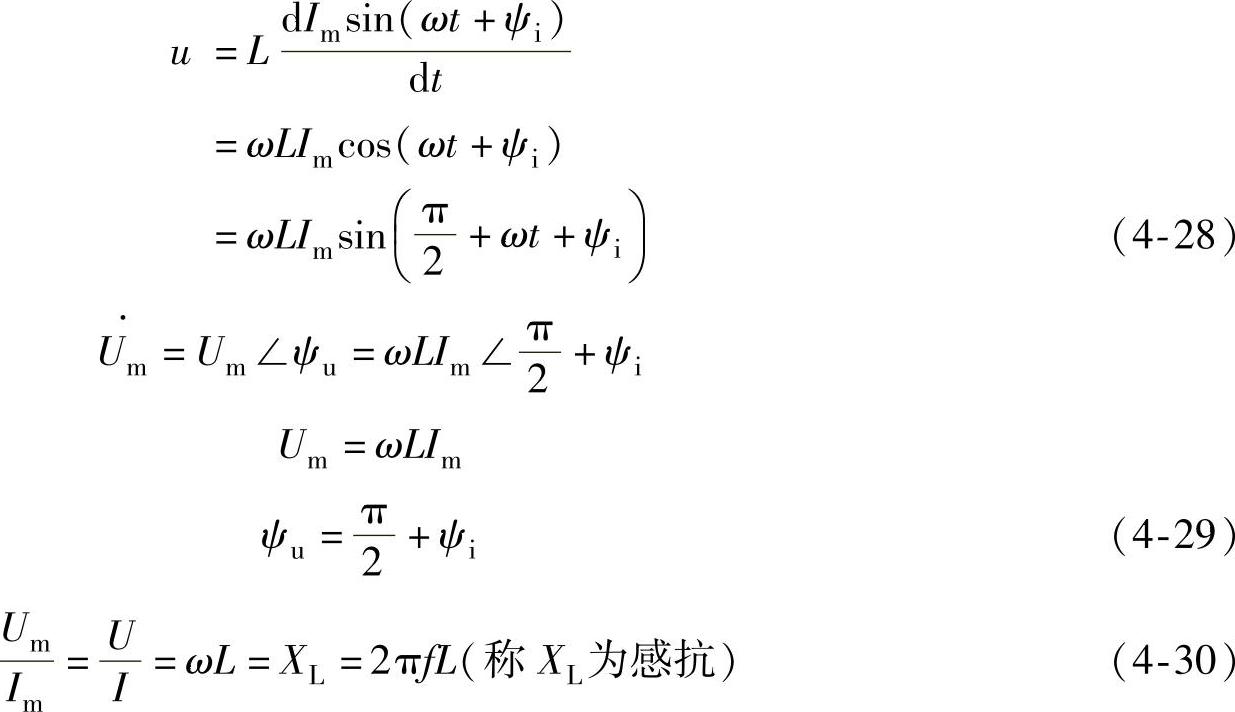
u、I的波形图与相量图,如图4-24b、c所示。
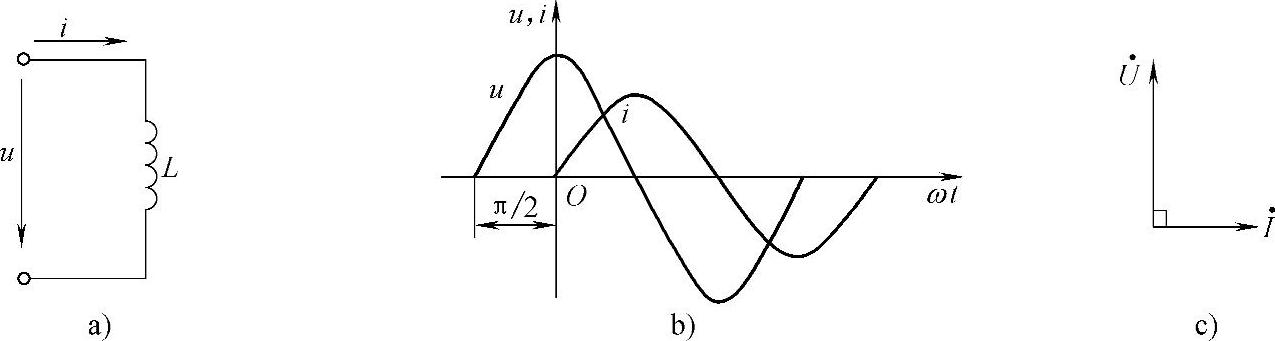
图4-24 纯电感电路
2.功率
瞬时功率:
1) 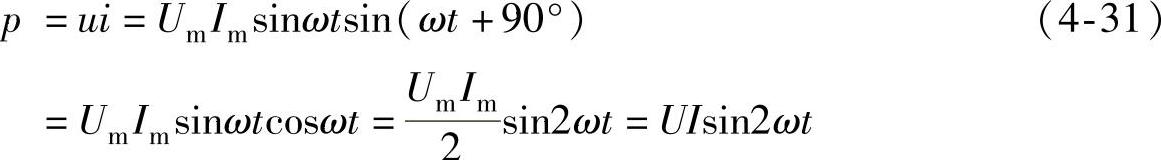
2)平均功率:
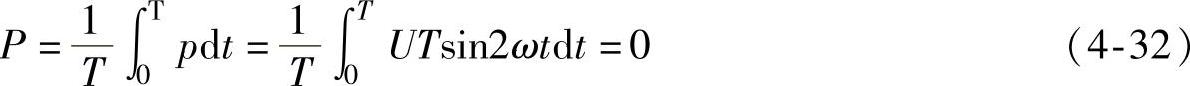
电感元件交流电路中,u比i超前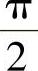 ;电压有效值等于电流有效值与感抗的乘积;平均功率为零,但存在着电源与电感元件之间的能量交换,所以瞬时功率不为零。为了衡量这种能量交换的规模,取瞬时功率的最大值,即电压和电流有效值的乘积,称为无功功率用大写字母Q表示,即
;电压有效值等于电流有效值与感抗的乘积;平均功率为零,但存在着电源与电感元件之间的能量交换,所以瞬时功率不为零。为了衡量这种能量交换的规模,取瞬时功率的最大值,即电压和电流有效值的乘积,称为无功功率用大写字母Q表示,即
Q=UI=I2XL=U2/XL (4-33)
电感对交流电的阻碍作用,可以简单概括为通直流,阻交流,通低频,阻高频。因此电感也被称为低通元件。
练一练
【例4.10】 已知一个自感系数为10mH的电感线圈,接在频率为50Hz的交流电中,其感抗为多少?接在频率为1MHz的交流电中。其感抗又为多少?
解:
交流电频率为50Hz时,电感的感抗为
XL=2πfL=2×3.14×50×10×10-3Ω=3.14Ω
交流电频率为1MHz时,电感的感抗为
XL=2πfL=2×3.14×1×106×10×10-3Ω=6.28×104Ω=62.8kΩ
接在直流电路中,其频率为0,故电感的感抗为
XL=2πfL=2×3.14×0×10×10-3Ω=0Ω
【例4.11】 一个10mH的电感器,接在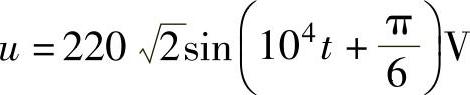 的交流电源上,
的交流电源上,
试求:(1)通过线圈的电流为多少?写出电流的解析式。
(2)电路的无功功率是多少?
解:
由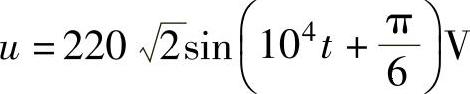 可知:
可知:
电源电压的有效值为U=220V,角频率ω=104rad/s,初相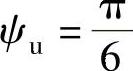 ,
,
线圈的感抗为 XL=ωL=104×10×10-3Ω=100Ω
电流的有效值为 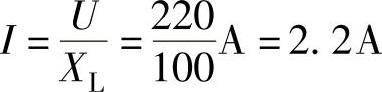
电流的初相为 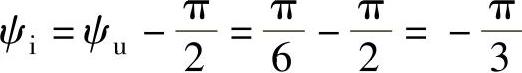
电流的解析式为 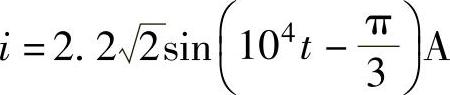
电路的无功功率为 QL=ULI=220×2.2var=484var
三、电容元件的交流电路
1.电压电流关系
1)瞬时关系: 如图4-25a所示

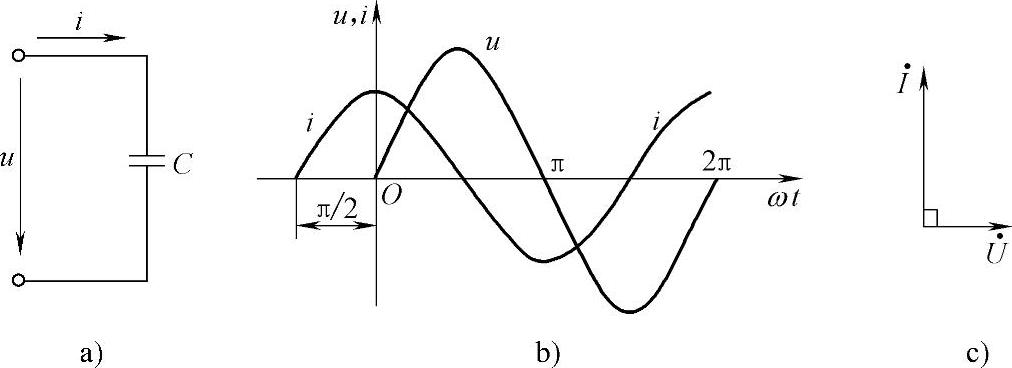
图4-25 纯电容电路
2)相量关系:在正弦交流电路中
令u=Umsin(ωt+ψu)即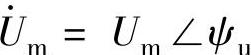 (4-35)
(4-35)
则
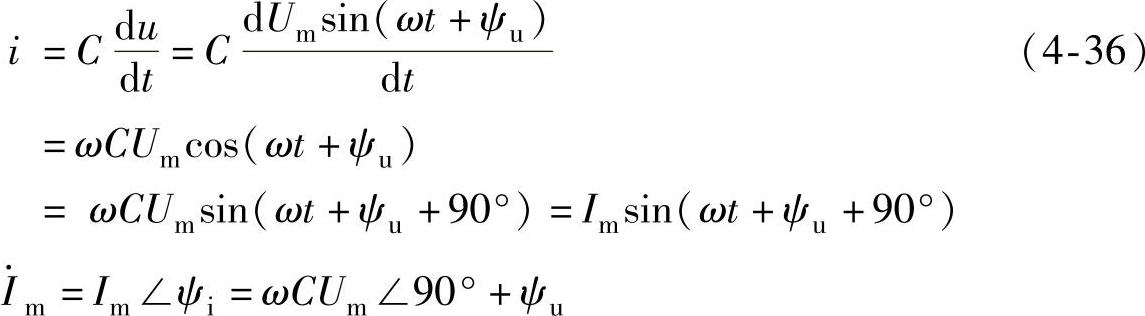
可见,Im=ωCUm=Um/XC (XC=1/ωC称为电容的容抗) (4-37)
φ=ψu-ψi=-90°
u、i的波形图和相量图,如图4-25b、c所示。
2.功率
1)瞬时功率。
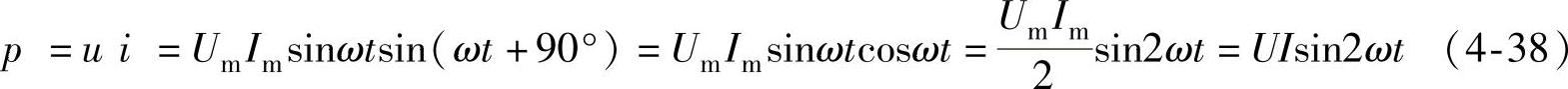
2)平均功率。
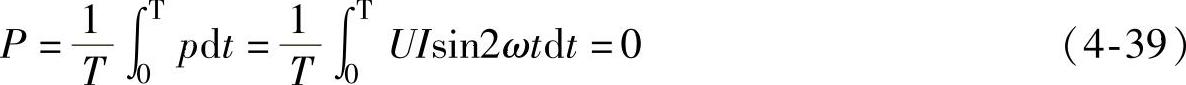
在电容元件电路中,在相位上电流比电压超前90°;电压的幅值(或有效值)与电流的幅值(或有效值)的比值为容抗XC;电容元件是储能元件,瞬时功率的最大值(即电压和电流有效值的乘积),称为无功功率,为了与电感元件区别,电容的无功功率取负值,用大写字母Q表示,即
Q=-UI=-I2XC=-U2/XC (4-40)
对于直流电,电容元件相当于开(断)路;对于交流电,电容器有“隔直流通交流,阻低频通高频”。
注:1)XC、XL与R一样,有阻碍电流的作用;
2)适用欧姆定律,等于电压、电流有效值之比;
3)XL与f成正比,XC与f成反比,R与f无关。对直流电f=0,L可视为短路,XC=∞,可视为开路。对交流电f愈高,XL愈大,XC愈小。
练一练
【例4.12】 已知一个10μF的电容器接到220V/50Hz的交流电中,其容抗为多大?接在频率为100kHz的交流电中,其容抗又为多少?接在直流电路中的容抗呢?
解:
交流电频率为50Hz时,电容的容抗为
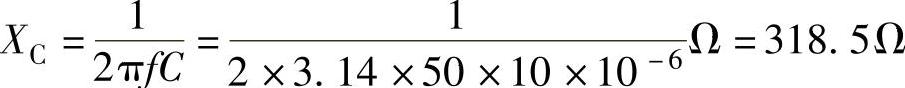
交流电频率为100kHz时,电容的容抗为
XL=2πfL=2×3.14×1×106×10×10-3=6.28×104Ω=62.8kΩ
接在直流电路中,其频率为0,故电容的容抗为
XL=2πfL=2×3.14×0×10×10-3Ω=0Ω
【例4.13】 一个10μF的电容器,接在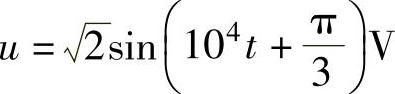 的交流电源上,
的交流电源上,
试求:(1)通过电容器的电流为多少?写出电流的解析式。
(2)电路的无功功率是多少?
解:
由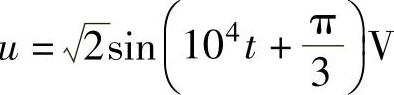 可知:
可知:
电源电压的有效值为U=1V,角频率ω=104rad/s,初相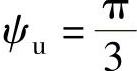 ,
,
电容的容抗为 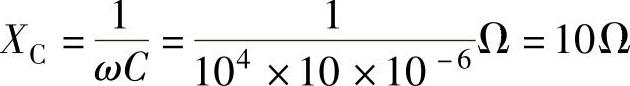
通过电容的电流为 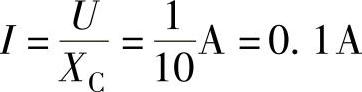 (https://www.xing528.com)
(https://www.xing528.com)
电流的初相为 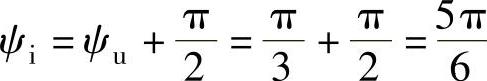
电流的解析式为 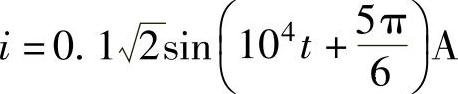
电路的无功功率为 QC=UCI=1×0.1var=0.1var
四、RLC串联电路分析
1.电压与电流的关系
uR=RImsinωt=URmsinωt (4-41)
1)瞬时值计算:设i=Imsinωt
则u=uR+uL+uC=RImsinωt+XLImsin(ωt+90°)+XCImsin(ωt-90°)
=Umsin(ωt+φ) (4-42)
其幅值为Um,与电流的相位差为φ。
2)相量计算:
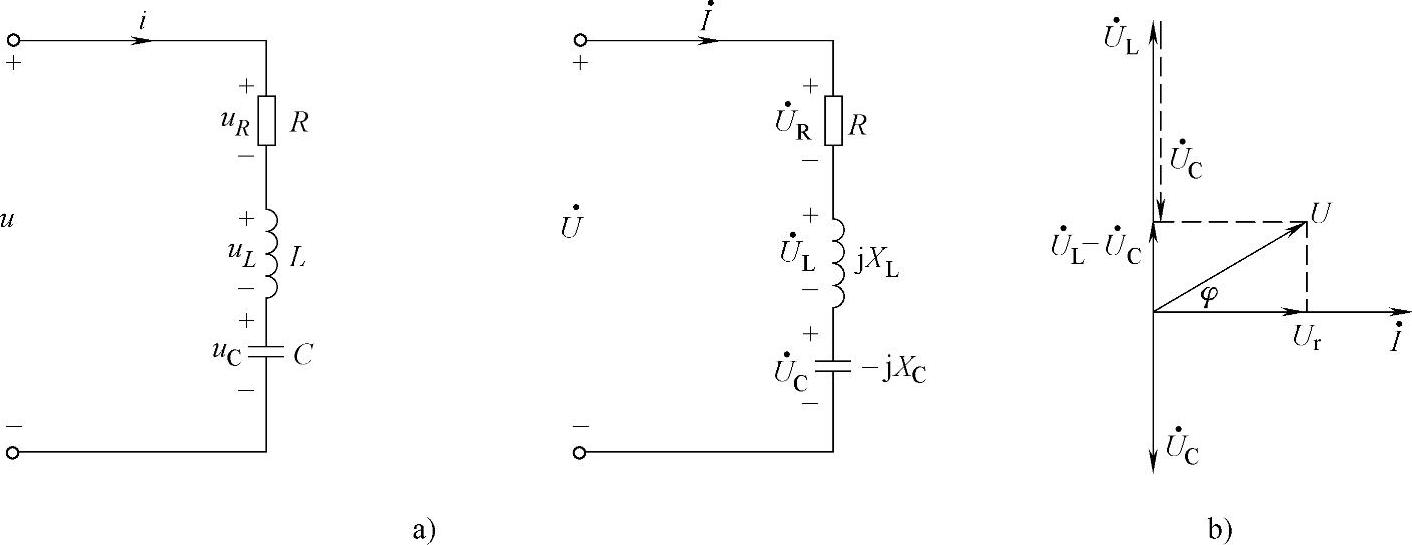
图4-26 RLC串联电路
如果用相量表示电压与电流的关系,则为
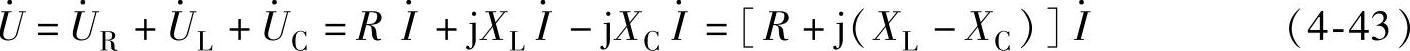
此即为基尔霍夫定律的相量形式。
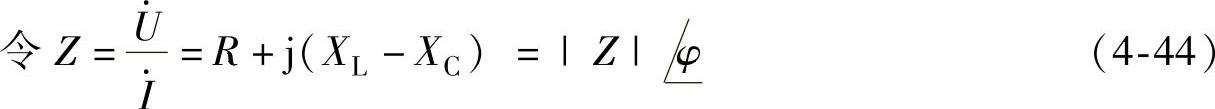
由图4-26b可见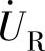 、
、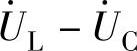 、
、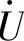 组成一个三角形,称电压三角形,电压u与电流i之间的相位差可以从电压三角形中得出,
组成一个三角形,称电压三角形,电压u与电流i之间的相位差可以从电压三角形中得出,
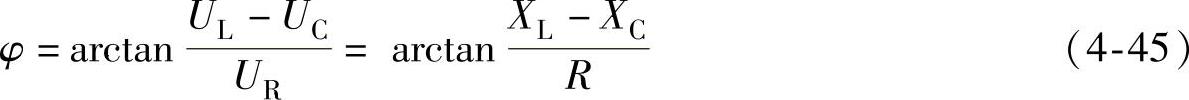
|Z|、R和(XL-XC)也可以组成一个直角三角形,称为阻抗三角形。
2.功率
1)瞬时功率:
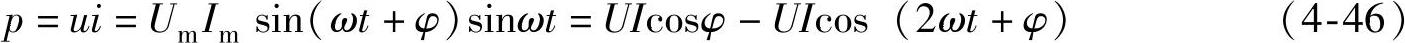
2)平均功率:
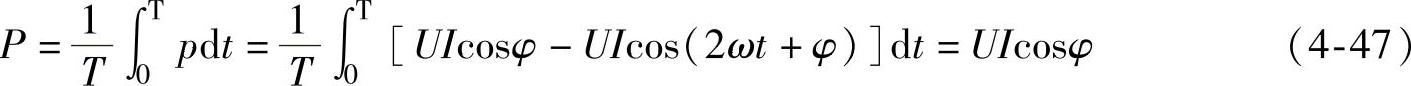
又称为有功功率,其中cosφ称为功率因数。
3)无功功率:Q=ULI-UCI=I2(XL-XC)=UIsinφ (4-48)
4)视在功率:S=UI称为视在功率
可见 
练一练
【例4.14】 已知某RLC串联电路中,电阻为30Ω,电感为127mH,电容为40μF,电路两端交流电压为u=311sin314tV,
试求:(1)电路的阻抗值为多少?
(2)电流的有效值是多少?
(3)各元件两端电压的有效值;
(4)电路的有功功率、无功功率和视在功率;
(5)判断电路的性质。
解:
由u=311sin314tV可知:
电源电压的有效值为U=220V,角频率ω=314rad/s,
(1)线圈的感抗为: XL=ωL=314×127×10-3Ω=40Ω
电容的容抗为: 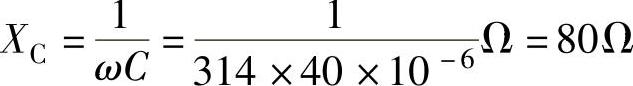
电路的阻抗为: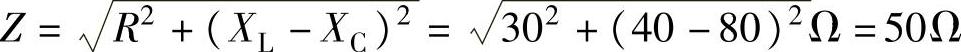
(2)电流的有效值为 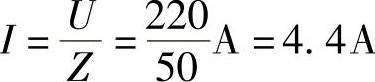
(3)各元件两端电压的有效值为UR=RI=30×4.4V=132V
UL=XLI=40×4.4V=176V
UC=XCI=80×4.4V=352V
(4)电路的有功功率、无功功率和视在功率为
P=I2R=4.42×30W=580.8W
Q=QL-QC=I2(XL-XC)=4.42×(40-80)var=-774.4var
S=UI=220×4.4V·A=968V·A
(5)电路的性质
因为XL<XC,QL<QC,即Q<0,表明该电路呈电容性。
五、电路中的谐振
由图4-26b的电压三角形可看出,当XL=XC时即电源电压u与电路中的电流i同相。这时电路中发生谐振现象。
1.串联谐振
谐振发生在串联电路中,称为串联谐振。
1)发生串联谐振的条件,XL=XC或
并由此得出串联谐振频率为

2)串联谐振的特征
①谐振时电路的阻抗最小,
②由于电源电压与电路中电流同相(φ=0),电路对电源呈现电阻性。
③由于XL=XC,于是UL=UC。而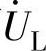 与
与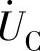 在相位上相反,互相抵消,因此电源电压
在相位上相反,互相抵消,因此电源电压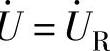 。
。
3)其具体应用是常用在收音机的调谐回路中。
2.并联谐振
谐振发生并联电路中,称为并联谐振。
1)并联谐振频率为 
2)并联谐振的特征:
①谐振时电路的阻抗为 
其值最大,即比非谐振情况下的阻抗要大。因此在电源电压U一定的情况下,电路的电流I将在谐振时达到最小值;②由于电源电压与电路中电流同相(φ=0),因此,电路对电源呈现电阻性;③当R≪ω0L时,两并联支路的电流近似相等,且比总电流大许多倍。
六、功率因数的提高
1.功率因数提高的意义
功率因数不高,根本原因就是由于电感性负载的存在。提高功率因数的实际意义为:①电源设备的容量能充分利用;②减小输电线路的功率损耗。
2.功率因数提高的方法
即在电感性负载电路上并联静电电容器(设置在用户或变电所中)。
1)电路图和相量图,如图4-27所示。
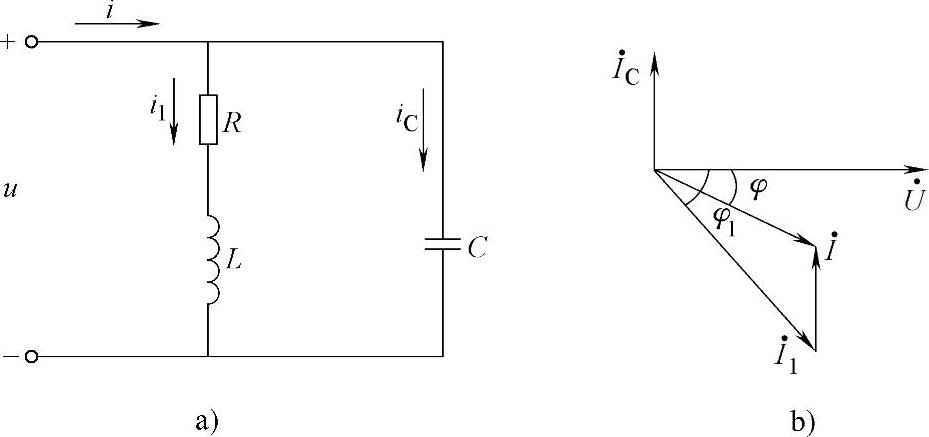
图4-27 功率因数提高的电路图和相量图
a)功率因数提高的电路图 b)功率因数提高的相量图
2)并联电容器的作用
并联电容器后,电感性负载的电流和功率因数均未发生变化,这时因为所加的电压和电路参数没有改变。但电路的总电流变小了;总电压和电路总电流之间的相位差φ变小了,即cosφ变大了。①并联电容器后,减小了电源与负载之间的能量互换;②并联电容器后,线路电流也减小了(电流相量相加),因而减小了功率损耗;③应该注意,并联电容以后有功功率并未改变,因为电容器是不消耗电能的。
巩固与提高
一、填空题
1.正弦电路不同于直流电路,在交流电路中不仅要考虑____,而且要考虑____和____。
2.电感对交流电的阻碍作用,可以简单概括为____:,因此电感也被称为____。
3.一个100μF的电容器接在50Hz的交流电中,其容抗为____;接在100kHz的交流电中,其容抗为____。一个100mH的电感线圈接在50Hz的交流电中,其感抗为____;接在20kHz的交流电中,其感抗为____。
4.电阻器是一种____元件,电感器和电容器是____元件。
5.把阻值为100Ω的电阻器接在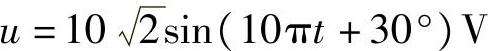 的交流电源上,则通过电阻器的电流大小为____,电流的解析式为____。
的交流电源上,则通过电阻器的电流大小为____,电流的解析式为____。
6.把100mH的电感线圈接在u=141sin(100πt-60°)V的电源上,则通过电感线圈的电流大小为____,电流的解析式为____。
7.把电容量为10μF的电容器接在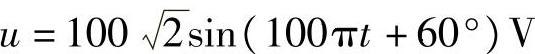 的电源上,则通过电容器的电流大小为____,电流的解析式为____。
的电源上,则通过电容器的电流大小为____,电流的解析式为____。
8.在RLC串联交流电路中,电源电压为100V,R=40Ω,XL=50Ω,XC=80Ω,则电路的阻抗Z=____,总电压与电流的相位差φ=____,电流的有效值I=____,电路的有功功率P=____,无功功率Q=____,视在功率S=____,该电路为____性质电路。
9.为了提高谐振电路回路的品质因素,如果信号源内阻较小,可以采用____谐振电路。如果信号源内阻很大,采用串联谐振电路会使____,常采用____谐振电路。
二、选择题
1.在纯电阻电路中,计算电流的公式为( )。
A.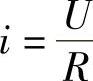 B.
B.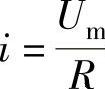 C.
C.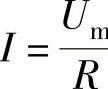 D.
D.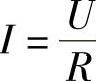
2.在一个RLC串联交流电路中,已知R=20Ω,XL=80Ω,XC=40Ω,则该电路呈( )。
A.电容性 B.电感性 C.电阻性 D.中性
3.功率表测量的是( )。
A.有功功率 B.无功功率 C.视在功率 D.瞬时功率
4.在RLC串联电路发生谐振时,下列说法正确的是( )。
A.Q值越大,通频带越宽
B.端电压时电容两端电压的Q倍
C.电路的电抗为零,则感抗和容抗也为零
D.总阻抗最小,总电流最大
5.交流电路中提高功率因素的目的是( )。
A.减小电路的功率消耗 B.提高负载的效率
C.增加负载的输出功率 D.提高电流的利用率
6.用示波器观察交流信号时,其耦合选择开关应拨在( )档。
A.AC B.DC C.GND D.无法确定
三、计算题
1.说说生活中交流电路中电阻元件、电感元件、电容元件的例子。
2.把L=51mH的线圈(线圈电阻极小,可忽略不计),接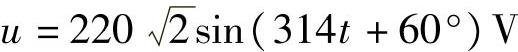 的交流电源上,试计算:
的交流电源上,试计算:
(1)XL。
(2)电路中的电流i。
(3)绘制电压、电流相量图。
3.把C=140μF的电容器,接在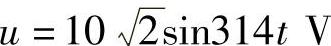 的交流电路中,试计算:
的交流电路中,试计算:
(1)XC。
(2)电路中的电流i。
(3)绘制电压、电流相量图。
4.用下列各式表示RC串联电路中的电压、电流,哪些是对的,哪些是错的?错的请改正过来。
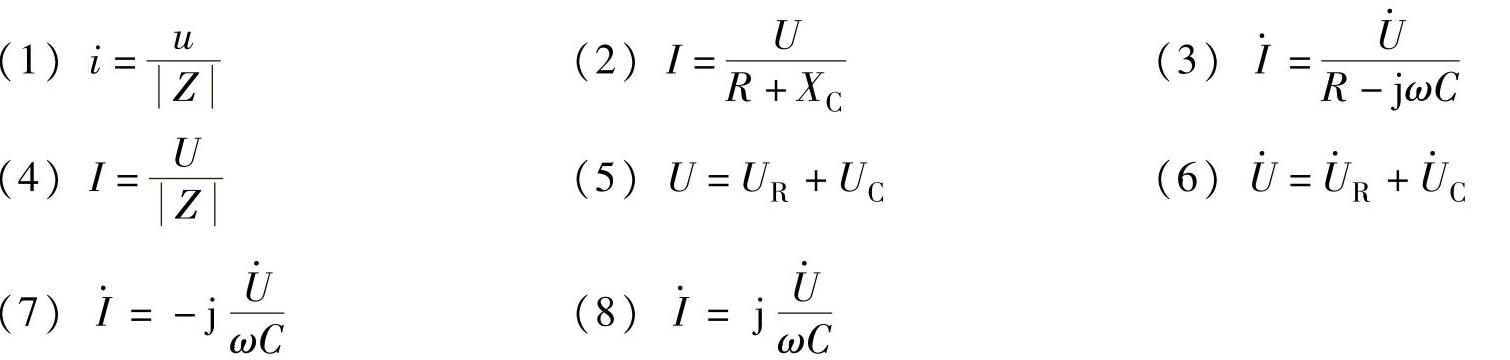
5.有一RC串联电路,接于50Hz的正弦电源上,如图4-28所示,R=100Ω,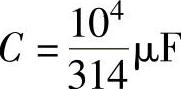 ,电压相量
,电压相量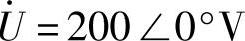 ,求复阻抗Z、电流
,求复阻抗Z、电流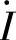 、电压
、电压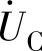 ,并绘制电压电流相量图。
,并绘制电压电流相量图。
6.如图4-29所示正弦交流电路,已知XC=50Ω,XL=100Ω,R=100Ω,电流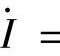
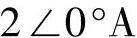 ,求电阻上的电流
,求电阻上的电流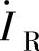 和总电压
和总电压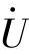 。
。
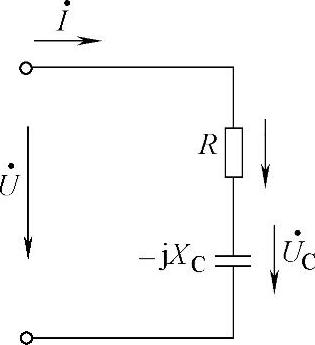
图4-28 计算题5的电路图
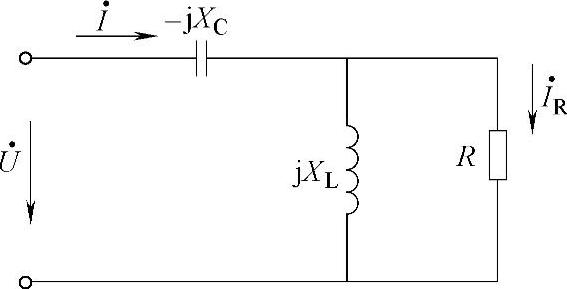
图4-29 计算题6的电路图
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




