轴间角与轴向伸缩系数优化

在斜轴测投影中，轴测投影面的位置可任意选定。只要投影方向与三个直角坐标面都不平行、不垂直，即投影方向与轴测投影面斜交成任意角度，所画出的轴测投影图就能同时反映物体三个方向的形状。因而斜轴测投影的轴间角和轴向伸缩系数^[1]可以独立变化，即都可以任意选定。

如果使斜轴测投影面P平行于坐标面XOZ，如图5-14所示，则不论投影方向与轴测投影面倾斜成任何角度，物体上平行于XOZ坐标面的表面，其轴测投影的形状都不变，即X，Z轴的轴向伸缩系数p=r=1，∠X1O1Z1=90°，但Y轴的轴向伸缩系数q以及O1Y1轴的方向，将随投影方向的变化而变化，且可任意选定。通过选择[5-13]二维码号可以观看。

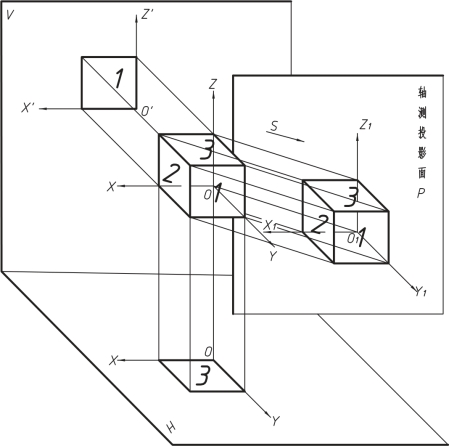
图5-14 斜二测图的形成

为了作图方便，并有较好的立体感，国标推荐的斜二等轴测图取Y轴的轴向伸缩系数q=0.5，轴间角∠X1O1Y1=∠Y1O1Z1=135°。作图时一般使O1Z1轴处于铅垂位置，这时O1Y1轴与水平线成45°，如图5-15（a）所示。

图5-15（b）（c）表示一个长方体的斜二测图。通过选择[5-14]二维码号可以观看。(www.xing528.com)

图5-16（a）表示一立方体的表面上分别有平行于相应坐标面的内切圆A，B，C，其斜二测图5-16（b）所示。其中平行于XOZ坐标面（即平行轴测投影面）的圆A，其斜二测图A1仍为圆的实形，而平行XOY，YOZ两坐标面的圆B及C的斜二测图则为椭圆。所以斜二测最大的优点是，凡平行于轴测投影面的图形都能反映实形，因此，它适合于在某一方向形状比较复杂的或有圆和曲线的物体的表达。通过选择[5-15]二维码号可以观看。

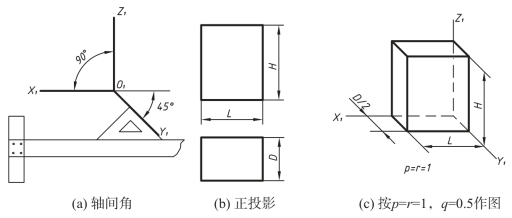
图5-15 斜二测图的轴间角和轴向伸缩系数

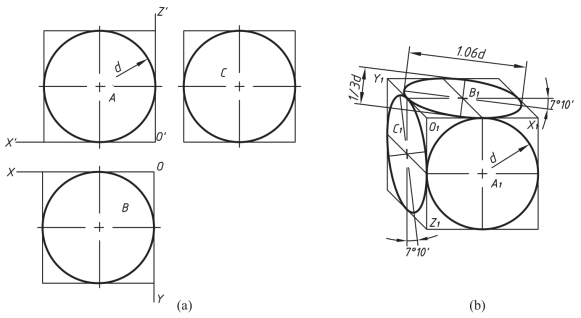
图5-16 坐标面上三个方向圆的斜二测图