切割式组合体形状与位置特征分析

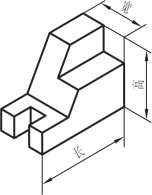
图3-12 导块立体图

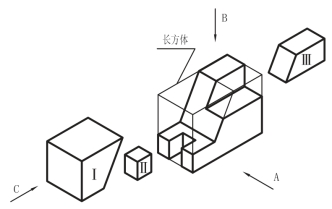
图3-13 导块形成过程

图3-12为一导块，通过选择[3-11]二维码号可以观看。从形体上看导块属于切割式的组合体。对切割为主的组合体可按其最大外形轮廓长、宽、高构建一个长方体，见图3-13。通过选择[3-12]二维码号可以观看。对照图3-12可以得到一个切割顺序。即在长方体上切去Ⅰ，Ⅱ，Ⅲ块后形成导块。由于形体与空间是互为表现的，没有足够的空间，形体无法被容纳。没有一定的形体作限定空间只能被感受为无限的宇宙空间的概念，空间只是一片空白，其本身没有什么意义。但形体出现以后，形体就占了空间，而那些未占据的空间就影响了形体的实际效果，对导块来讲长方体是空间，被切去的三块是它未占据的空间，称为导块的补形体。因此在长方体空间内导块的形状由其补形体决定。于是，对切割式的组合体，其形状与相对位置特征可由补形体的形状特征和相对位置特征来表示。即从某方向看，有形状特征的补形体数与补形体总数之比称作组合体在该方向的形状特征系数S。由图3-13可知三块补形体均为A向拉伸形体，于是可得导块A向形状特征系数，同理可分析出。对导块的相对位置特征系数的确定，应先计算确定补形体与相关形体从某方向看到的两种位置关系的独立尺寸数之和P。相关形体概念见图3-14。通过选择[3-13]二维码号可以观看。

图3-14 相关形体(www.xing528.com)

将定义为相对位置特征系数，其中n为补形体总数。而将L=1 Lr作为导块的相对位置特征系数。

对A 向确定补形体与其相关形体位置的独立尺寸数为：

（Ⅰ）（Ⅰr）=0，（Ⅱ）（Ⅱr）=0，（Ⅲ）（Ⅲr）=0，由此得P=0，LA=1；

对B向 （Ⅰ）（Ⅰr）=0，（Ⅱ）（Ⅱr）=0，（Ⅲ）（Ⅲr）=1，由此得P=1；

对C向 （Ⅰ）（Ⅰr）=0，（Ⅱ）（Ⅱr）=0，（Ⅲ）（Ⅲr）=1，由此得P=1；

由上述分析可知A向的形状特征与相对位置特征最为显著。应该指出，形状特征与相对位置特征的计算有时较为烦琐。事实上，当物体比较简单时，凭借经验也可选定好的主视图投影方向，因此可以经验与计算相结合。当经验难以有效判定时，辅以计算可使所选主视图投影方向有理论依据。