机械设计硕士入学考试试题及解答 - 上海大学

1-1　是非题

1.√；2.×；3.√；4.×；5.×；6.×；7.×；8.×；9.×；10.×。

1-2　单项选择题

1.C；2.D；3.A；4.A；5.B；6.C；7.B；8.C；9.B；10.B；11.A；12.A；13.B；14.A；15.A。

1-3　简答、证明题

1.答：N1点为r=C的极限应力点，零件失效是塑性变形。N2点为σm=C的极限应力点，零件失效是疲劳断裂。G点为σmin=C的极限应力点，零件失效可能是塑性变形，也可能是疲劳断裂。

2.答：（1）轮1主动时，轮2轮齿表面的接触应力呈脉动循环变化（每转一周，同一侧齿面啮合一次），轮2齿根弯曲应力呈对称循环变化（每转一周，同一截面一次受拉、一次受压）。轮2主动时，轮2轮齿表面的接触应力呈脉动循环变化（每转一周，同一侧齿面啮合两次），轮2齿根弯曲应力呈脉动循环变化（每转一周，同一截面二次受拉或二次受压）。

（2）设轮1主动时，轮2表面的接触应力循环次数为N1；设轮2主动时，轮2表面的接触应力循环次数为N2。则有2N1=N2，按有限寿命考虑，就有接触疲劳寿命系数KHN2＜KHN1，而[σ]H=σHlimKHN/S，就有[σ]H2＜[σ]H1，因而轮1主动时，轮2接触疲劳强度高。

（3）设轮1主动时，轮2齿根弯曲应力循环次数为N1；设轮2主动时，轮2齿根弯曲应力循环次数为N2。按无限寿命考虑，就有弯曲疲劳寿命系数KFN1=KFN2=1。并且由于轮1主动时，轮2齿根弯曲应力是对称循环变化，轮2主动时，轮2齿根弯曲应力是脉动循环变化，所以有σFlim1=0.7σFlim2，由[σ]F=KFNσlim/S得出：[σ]F2＞[σ]F1，因而轮2主动时，轮2弯曲疲劳强度高。

3.答：影响链速不均匀性的主要参数是链轮齿数z和链节距p。采用较多的小链轮齿数和较小的链节距可减轻不均匀性的程度。

4.答：带在减速传动中带的不同截面上的应力分布情况如图2-1-1所示。

图2-1-1

拉应力σ1和σ2主要由预紧力F0、传动的功率P及带的速度υ决定；离心应力σc主要由带的速度υ决定；弯曲应力σb主要由带轮直径dd决定。

5.答：蜗杆传动的总效率η=η1η2η3，其总效率主要取决于啮合效率。令

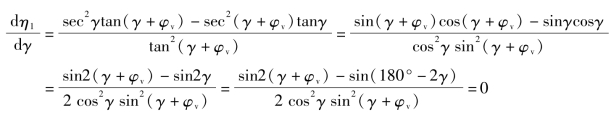
则有：sin2（γ+φv）-sin（180°-2γ）=0，即2（γ+φv）=180°-2γ，4γ=180°-2φv，即γ=45°-。

又因为γ＜45°-为“-”。所以当γ=45°-时，啮合效率最高。

6.证明：在两块平板中取做层流运动的油膜微单元体dxdydz进行分析，如图2-1-2所示，列出油膜微单元体力平衡方程式为

图2-1-2

整理后得：。

将牛顿内摩擦定律（黏性定律）τ=-η带入上式，得。

对上式变量y积分后为

再次对变量y积分后为

将初始条件u=|y=0=υ，u|y=h=0代入上式，得

所以

润滑油沿x方向流经单位宽度任意剖面的流量为

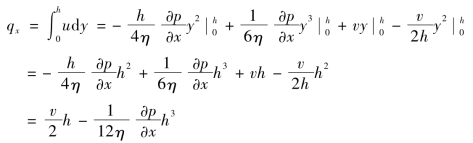
设油压p=pmax处的油膜厚度h=h0，则有。

根据液体流动连续性方程就有υ 2h-1 12 η∂p∂xh3=υ 2h0将上式整理后可得液体动压润滑一维雷诺方程式∂p∂x=6ηυh-h0 h 3

1-4　计算分析题(www.xing528.com)

1.解：根据题意，螺钉材料的许用应力为

[σ]=0.8σs=0.8×240=192（MPa）

由可得螺钉的预紧力为

由2F0f=KsF可得允许的曳引力为

2.解：两轴承的派生力分别为

由图2-1-3可得：Fd2+FA=250+750=1000（N）＞Fd1，故轴承1被“压紧”，轴承2被“放松”。两轴承所受的轴向力分别为

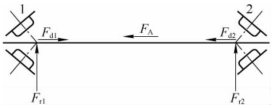
图2-1-3

Fa1=FA+Fd2=1000（N），Fa2=Fd2=250（N）

因为=0.625＞e，所以X1=0.4，Y1=1.6。

因为=0.3125＜e，所以X2=1，Y2=0。

两轴承的当量动载荷分别为

P1=fp（X1Fr1+Y1Fa1）=1.2×（0.4×1600+1.6×1000）=2688（N）

P2=fp（X2Fr2+Y2Fa2）=1.2×（1×800+0）=960（N）

两轴承的寿命分别为

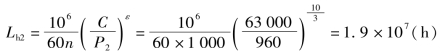
3.解：（1）低速级小齿轮z3轮齿的螺旋线方向应为左旋，才能保证中间轴Ⅱ上两齿轮的轴向力相反，如图2-1-4所示。

图2-1-4

（2）由Fa2=Fa3得：Ft2tanβ2=Ft1tanβ1=Ft3tanβ3，即tanβ3=tanβ1。

T2=，因不计摩擦效率，则有T2=

T3，故有，即tanβ3=tanβ1=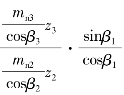

即sinβ3=×sin12°7′43″

所以　　β3=10.476°=10°28′35″

（3）作用在齿轮1上的转矩为

作用在齿轮2上的转矩为

齿轮2所受的圆周力、轴向力和径向力分别为

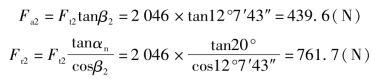
齿轮2啮合点上三个分力的方向如图2-1-4所示。