1.如图7-1所示简单RC并联电路,若以电流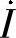 为激励,电压
为激励,电压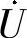 为响应,求网络函数H(jω)、截止角频率ωC,并定性画出幅频特性曲线。
为响应,求网络函数H(jω)、截止角频率ωC,并定性画出幅频特性曲线。

图7-1 题1图
解:由于所分析的网络函数为电路输入阻抗,由阻抗并联关系得
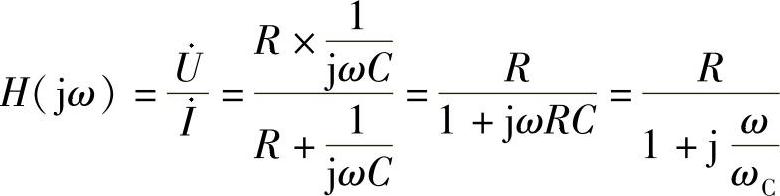
可推得电路幅频特性为
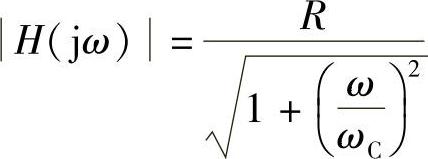
式中,电路截止角频率ωC为

幅频特性曲线如图7-2所示。
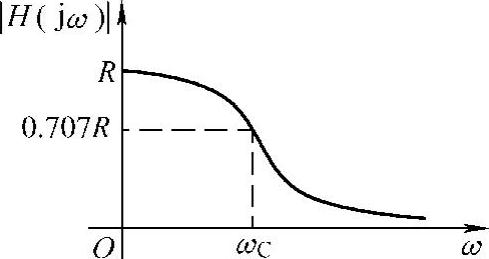
图7-2 题1解图
2.试求出图7-3所示电路的电压传输函数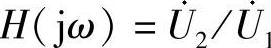 。
。
解:由分压公式得电压传输函数为
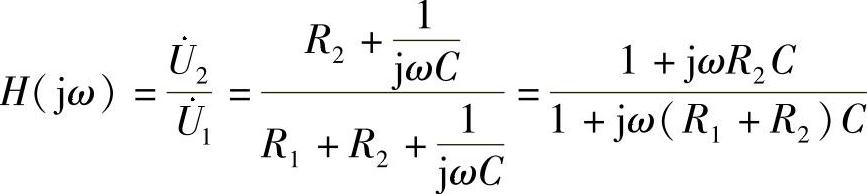
3.试求出图7-4所示电路的电压传输函数H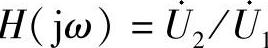 。
。

图7-3 题2图
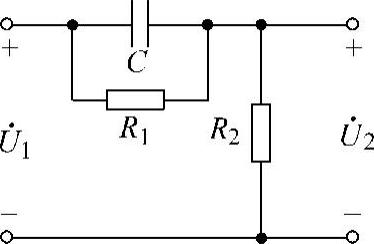
图7-4 题3图
解:由分压公式得电压传输函数为

4.求图7-5所示电路的电压传输函数 。
。
解:由分压公式可得电压传输函数为


图7-5 题4图
5.在图7-6所示电路中,L=2H,C=0.1F,R=10Ω:
(1)求电压传输函数H 。
。

图7-6 题5图
(2)若u1(t)=(1+10cost+10cos3t)V,求稳态响应u2(t)。
解:(1)电压传输函数为

代入元件参数有

(2)把激励电压u1(t)视为三个独立电压源的串联,分别令u′1(t)=1V,u″1(t)=10costV,u‴1(t)=10cos3tV,即
u1(t)=u′1(t)+u″1(t)+u‴1(t)
由于上述三个电压源的激励频率各不相同,就整个电路而言,不符合单一频率的条件,故不能直接使用相量法。可根据线性电路叠加定理,借助网络函数分别求出三个不同频率的电源单独作用时产生的响应分量,然后叠加得到电路的稳态响应u2(t)。
①u′1(t)=1V单独作用时,激励频率ω0=0(直流激励)

产生的响应分量u2′(t)=1×H(j0)=1×1V=1V
②u″1(t)=10costV单独作用时,激励频率ω0=1rad/s
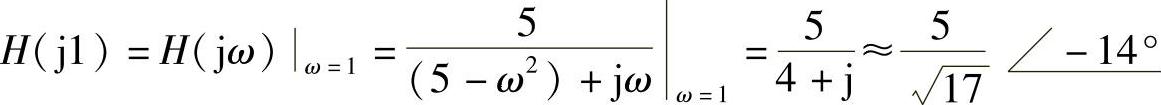
产生的响应分量为

③u‴1(t)=10cos3tV单独作用时,激励频率ω0=3rad/s
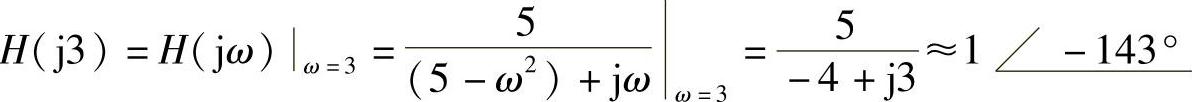
产生的响应分量为
u‴2(t)=10×H(j3)cos[3t+φ(3)]=10×1cos(3t-143°)V=10cos(3t-143°)V
④根据叠加定理,u1(t)作用时,电路的稳态响应u2(t)为

6.求图7-7所示电路的电压传输函数 。
。
解:图7-7所示电路的去耦相量模型如图7-8所示,有
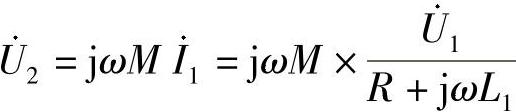
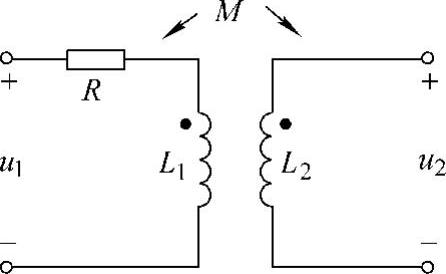
图7-7 题6图

图7-8 题6解图
则电压传输函数H(jω)为

7.电路如图7-9所示
(1)写出电压传输函数 。
。
(2)若u1(t)=2cos(3t)V,欲使正弦稳态响应为零,求LC的约束条件。
解:(1)电压传输函数为


图7-9 题7图
(2)u1(t)=2cos(3t)V时,欲使正弦稳态响应为零,由电压传输函数可知电路的约束条件应为
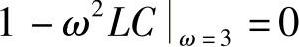
即
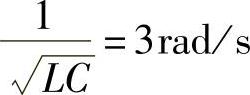
即LC并联谐振电路对角频率为ω=3rad/s的信号电压u1(t)=2cos(3t)V发生并联谐振。
8.如图7-10所示RLC串联谐振电路,已知电源电压Us=1V,频率f=1MHz,调节电容C使电路达谐振时,回路电流I0=100mA,电容电压UC0=100V。求电路参数R、L、C及回路的品质因数Q与通频带BW。

图7-10 题8图
解:电路达到串联谐振状态时,电源频率与电路谐振频率f0两者相等,则有
f0=f=1MHz
根据串联谐振的特点,有
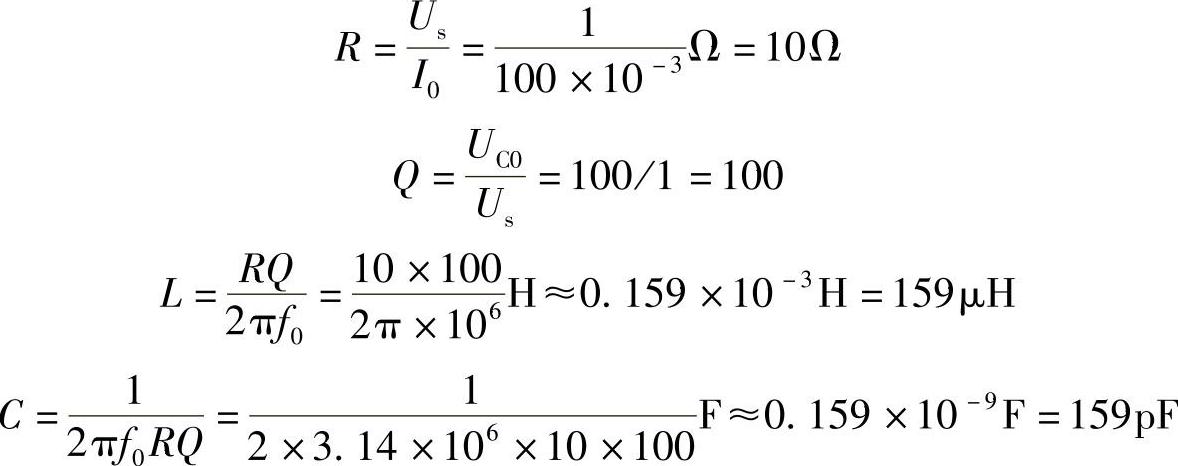
而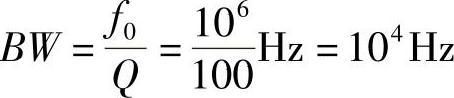
或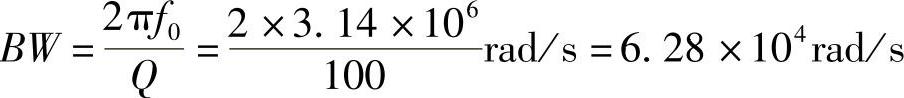
9.如图7-11所示串联谐振电路,已知L=50μH,C=200pF,回路品质因数Q=50,电源电压有效值Us=1mV。求:电路的谐振频率f0、谐振时回路电流的有效值I0、电容电压有效值UC0。
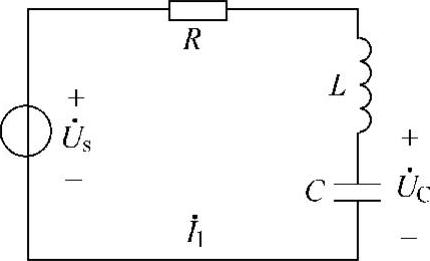
图7-11 题9图
解:电路的谐振频率f0为
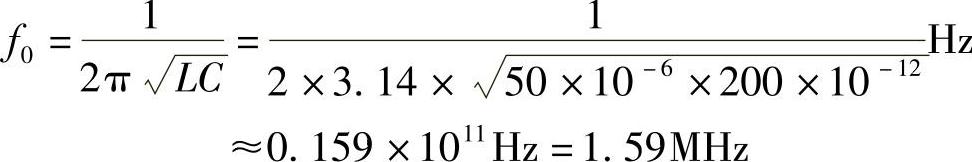
串联谐振时电容电压有效值UC0为
UC0=QUs=50×1×10-3V=5×10-2V=50mV
谐振时回路电流有效值I0为

10.图7-12所示电路是应用串联谐振原理测量线圈电阻r和电感L的电路。已知R=10Ω,C=0.1μF,保持电源电压有效值Us=1V不变,只改变电源频率f,同时用电压表测量电阻R两端的电压UR,当f=800Hz时,URmax=0.8V,试求电阻r和电感L。
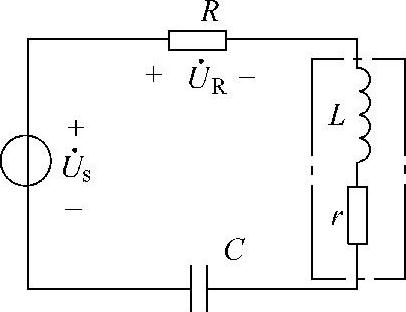
图7-12 题10图
解:谐振时LC串联电路相当于交流短路,外加电源电压全作用于纯电阻两端,此时,电路谐振电流有效值I0的表达式为
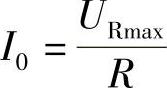
而线圈电阻r为
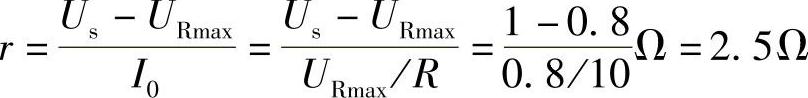
线圈电感L为
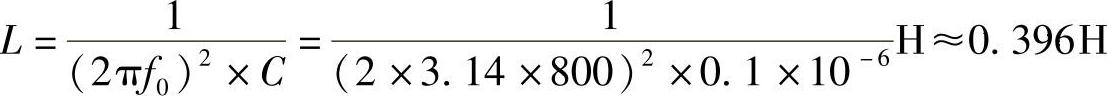
11.某RLC串联谐振电路,已知外加电源内阻为零,电源电压us(t)=100cos(ω0t)mV,ω0为电路谐振角频率,C=400pF,电阻R上消耗的功率为5mW,电路的通频带BW=4×104rad/s,试求L、ω0、Ucm。
解:串联谐振时,外加电源电压全作用于纯电阻R两端,此时电阻消耗的功率P为
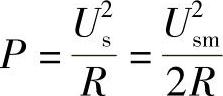
由此可求得电阻R为

根据公式

有

电路谐振角频率ω0为
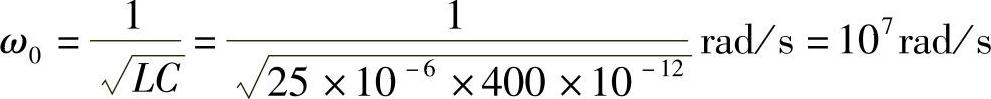
谐振时电容电压最大值Ucm为
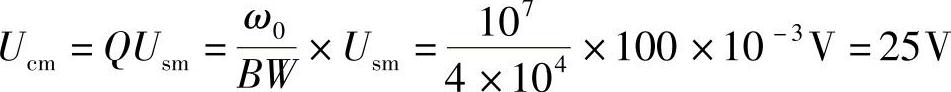
12.电路如图7-13所示,已知R=15Ω,L=100mH,is(t)=(5+3cosω0t+cos2ω0t)A,ω0=100rad/s,输出u(t)为只含直流分量和角频率为2ω0的二次谐波分量,求电容C。
解:串联谐振时,LC串联电路相当于交流短路,其两端电压为零,所以,欲使输出u(t)不含角频率为ω0的谐波分量,LC串联电路的谐振频率应为ω0=100rad/s。
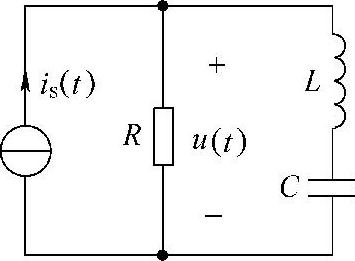
图7-13 题12图
因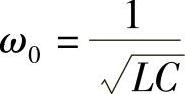
则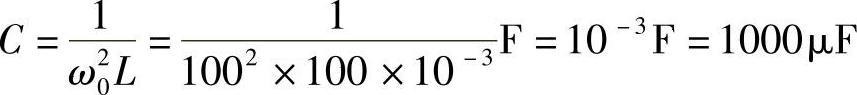
13.收音机的接收电路如图7-14所示,已知可变电容C的容量为30~305pF,问欲使最低谐振频率为530kHz,线圈的电感量应是多少?接入线圈后,该接收电路的调谐频率范围是多少?

图7-14 题13图
解:对天线上感应出的电信号来说,图7-14所示电路中由L、C组成的接收电路实质上是一个串联谐振回路,根据公式
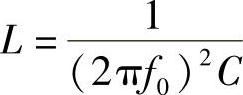
在调节可变电容C的容量至最大值305pF时,欲使最低谐振频率f0min为530kHz,线圈的电感量应为
 (https://www.xing528.com)
(https://www.xing528.com)
当可变电容C的容量取最小值30pF时,最高谐振频率f0max为
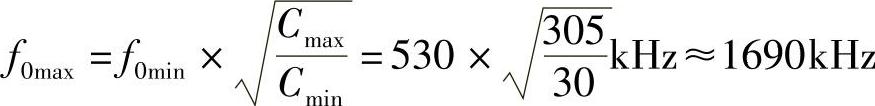
故接收电路的调谐频率范围为530~1690kHz。
14.并联谐振电路如图7-15所示,已知R=40kΩ,C=250pF,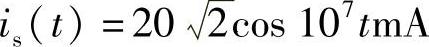 ,求谐振时电流iL(t)、iX(t)及电阻R消耗的功率P。
,求谐振时电流iL(t)、iX(t)及电阻R消耗的功率P。
解:并联谐振电路处于谐振状态,电路谐振角频率为
ω0=107rad/s
电路品质因数Q为
Q=Rω0C=40×103×107×250×10-12=100

图7-15 题14图
谐振时电感电流(有效值或最大值)为激励电流的Q倍,相位上滞后激励电流90°,则有
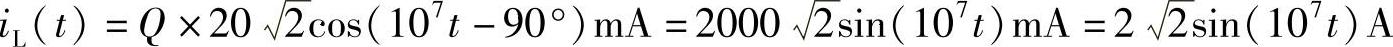
由于谐振时电感电流和电容电流相位相反、大小相等且为激励电流的Q倍,故流经LC并联电路的电流为零,即
iX(t)=0
谐振时LC并联电路相当于开路,电源只向电阻支路提供电流,则电阻R消耗的功率为
P=I2sR=(20×10-3)2×40×103W=16W
15.如图7-16所示并联谐振电路,已知r=40Ω,L=10mH,C=400pF。
(1)求谐振频率f0、谐振阻抗Z0、特性阻抗ρ和电路品质因数Q。
(2)若输入电流 ,求谐振时电容电压UC0和电流IC0。
,求谐振时电容电压UC0和电流IC0。

图7-16 题15图
解:(1)图7-16所示实际并联谐振电路的谐振频率f0近似为
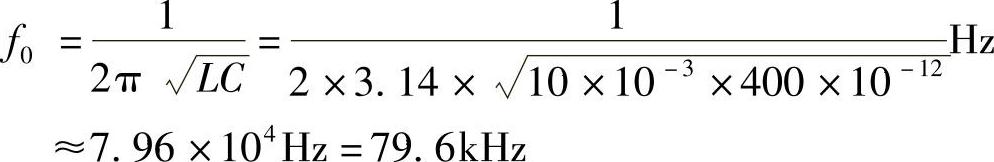
谐振阻抗Z0为纯电阻,有
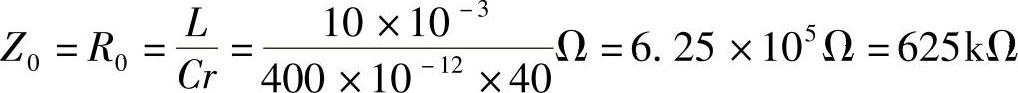
特性阻抗ρ为
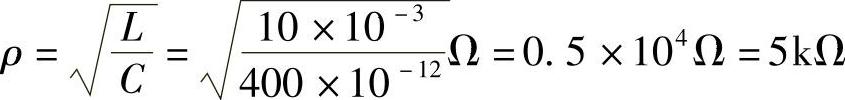
谐振时电路品质因数Q为

(2)谐振时电容电压UC0和电流IC0分别为
UC0=I×Z0=10×10-6×6.25×105V=6.25V
IC0=Q×I=125×10×10-6A=1.25×10-3A=1.25mA
16.电路如图7-17所示:
(1)当电源角频率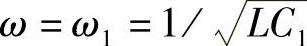 时,哪些电路相当于短路,哪些相当于开路?
时,哪些电路相当于短路,哪些相当于开路?
(2)有人认为在另一频率ω2,图7-17c、图7-17d所示两电路相当于开路,是否可能?若有可能,ω2是大于ω1还是小于ω1?
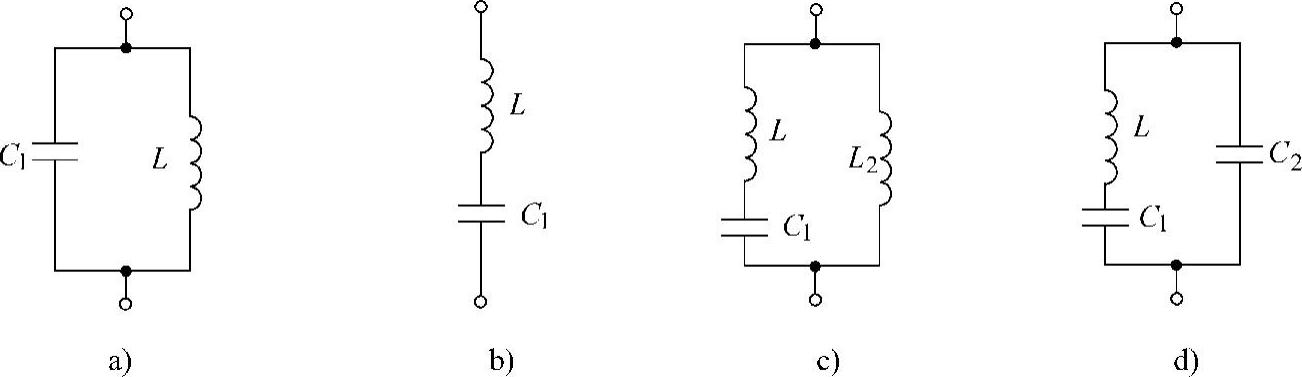
图7-17 题16图
解:(1)串联谐振时,LC串联电路相当于交流短路。并联谐振时,LC并联电路相当于交流开路。当电源角频率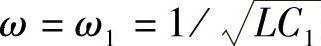 时,图7-17a所示电路显然发生并联谐振,相当于开路。而在其他电路中,LC1串联电路(或支路)发生串联谐振,从对外端口来看则相当于交流短路。
时,图7-17a所示电路显然发生并联谐振,相当于开路。而在其他电路中,LC1串联电路(或支路)发生串联谐振,从对外端口来看则相当于交流短路。
(2)图7-17c、图7-17d所示两电路若发生并联谐振,则整个电路对外相当于开路。
对于图7-17c所示电路,由端口等效导纳为零可以推得发生并联谐振的谐振角频率ω2为 且
且
从物理概念角度不难理解上述结果,因为只有在并联的LC1串联支路呈现容性时,图7-17c所示电路才可能发生并联谐振,LC1串联支路呈现容性显然要求ω2<ω1。
而对图7-17d所示电路,由端口等效导纳为零可以推得发生并联谐振的谐振角频率ω2为 且
且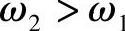
上述结果也不难理解,若使图7-17d所示电路发生并联谐振,LC1串联支路必须呈现感性,显然要求ω2>ω1。
17.电路如图7-18所示,电源电压us(t)=(3+2cos10t+cos30t)V,求u(t)。
解:激励电压us(t)可视为三个独立电压源的串联,分别为us1(t)=3V,us2(t)=2cos(10t)V,us3(t)=cos(30t)V,即
us(t)=us1(t)+us2(t)+us3(t)
由于上述三个电压源的激励频率各不相同,就整个电路而言,不能直接使用相量法。可分别求出三个不同频率电源单独作用时产生的响应分量,然后根据线性电路叠加定理求出电路的响应u(t)。

图7-18 题17图
(1)us1(t)=3V单独作用时,因为属于直流激励,电路中电感视为短路,电容视为开路,不难看出产生的响应分量u′(t)为
u′(t)=0V
(2)电路中两电感分别用L1(电感量L1=0.4H)和L2(电感量L2=0.05H)表示,电容用C表示,其中L1C并联电路的局部并联谐振角频率ω01为

当us2(t)=2cos(10t)V单独作用时,因L1C并联谐振,可视为开路,故由us2(t)产生的响应分量u″(t)为
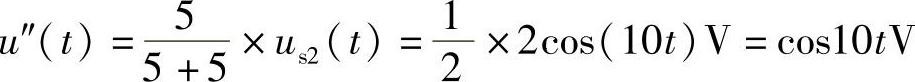
(3)电路中,L1C并联电路与电感L2串联,其串联谐振频率ω02为
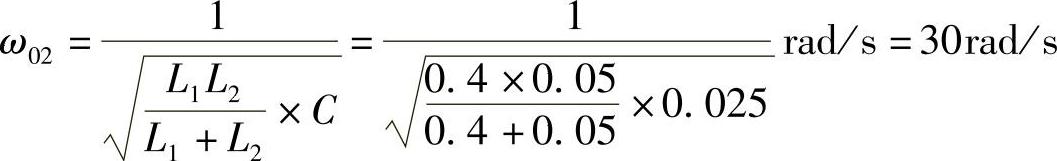
当us3(t)=cos(30t)V单独作用时,显然由L1C并联电路与电感L2串联共同组成的支路处于串联谐振状态,其谐振阻抗为零,因而呈现交流短路,不难看出us3(t)产生的响应分量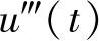 为
为

综合上述分析结果,可求出电路的响应u(t)为
u(t)=u′(t)+u″(t)+u‴(t)=cos(10t)V
18.图7-19所示电路为收音机中频放大器的等效电路,信号电流源is(t)含有多个频率分量,其中最低频率为455kHz,最高频率为475kHz,信号源内阻Rs=90kΩ,并联谐振回路作为该放大器的负载,已知L=293μH,C=400pF,空载回路品质因数Q=105。
(1)若回路直接与信号源相接,输出信号u(t)是否会有失真,为什么?
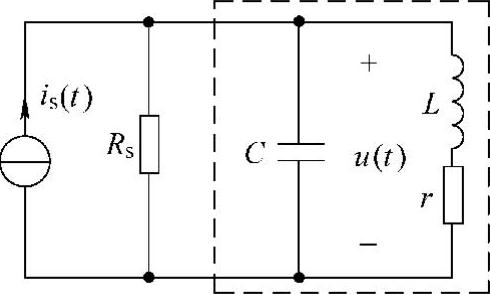
图7-19 题18图
(2)欲减小输出信号失真,可采取何种简便措施?
解:实际电信号总是占有一定的频带宽度,从保证传输信号不失真的前提出发,电路的通频带不能小于信号的带宽。
(1)根据题意,输入信号is(t)包含的频率分量中,最低频率fmin和最高频率fmax分别为
fmin=455kHz,fmax=475kHz
输入信号带宽BW信则为
BW信=fmax-fmin=(475-455)kHz=20kHz
输入信号的中心频率fs0为

电路谐振频率f0是
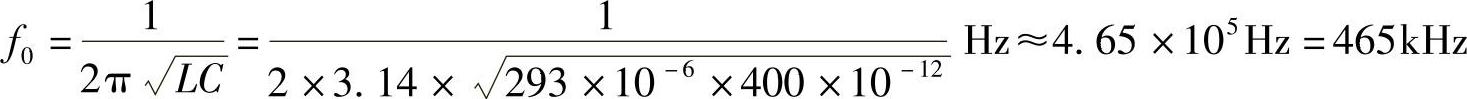
空载回路谐振电阻R0为
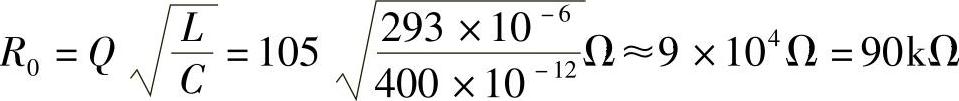
考虑电源内阻Rs的影响,总的等效电阻R0′为
R0′=R0∥Rs=(90∥90)kΩ=45kΩ
此时电路的有载品质因数Q′为

而整个电路的通频带宽BW电路为
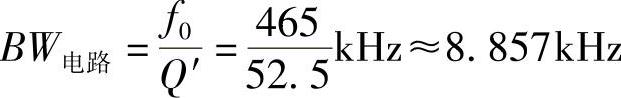
显然,在输入信号中心频率fs0位于电路谐振频率f0处(即fs0=f0)的情况下,由于电路通频带小于信号带宽(即BW电路<BW信),致使信号中的部分主要频率分量处在电路通频带之外而被滤掉,所以回路直接与信号源相接,输出信号u(t)会有失真。
(2)欲减小输出信号失真,则电路的通频带不能小于信号的带宽,简便措施就是在回路两端并联一个大电阻,通过降低电路的有载品质因数,拓宽电路的通频带到至少与信号的带宽相等。假设并联的大电阻为RL,考虑并联电阻RL后电路的有载品质因数为Q″、电路通频带为BW′电路和谐振时总等效电阻为R″0,则并联电阻RL具体计算如下:
由
可得

则谐振时总等效电阻R″0为
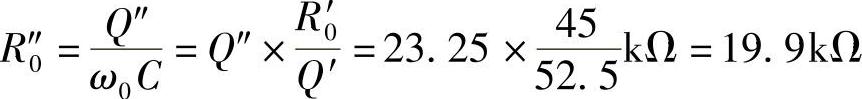
再由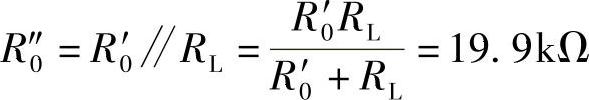
可计算得
RL=35.7kΩ
所以,要使电路具有满足传输信号所需的电路带宽,有效减小输出信号失真,在回路两端并联的电阻阻值应不大于35.7kΩ。
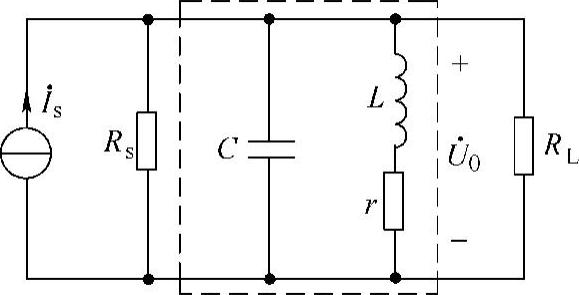
图7-20 题19图
19.图7-20所示并联谐振电路处于谐振状态。已知空载品质因数Q=105,L=586μH,C=200pF,电源内阻Rs=180kΩ,负载电阻RL=180kΩ, 。求回路两端电压U0、电路通频带BW。
。求回路两端电压U0、电路通频带BW。
解:为了简化分析计算,高Q条件下谐振频率ω0处,可将图7-20所示实际并联谐振电路等效成如图7-21所示的高Q等效电路。等效电路中R0为

考虑到电源内阻和负载电阻的影响,总的等效电阻为
R0′=Rs∥R0∥RL=(180∥180∥180)kΩ=60kΩ
谐振时回路两端电压U0为
U0=IsR0′=3×10-3×60×103V=180V
考虑到电源内阻和负载电阻的影响,整个电路的品质因数为
Q′=R0′×ω0C
则电路通频带BW为


图7-21 题19解图
20.电路如图7-22所示,已知r=10Ω,L=10mH,在外加电压大小和频率不变的情况下,调节电容C1,使电路总电流有效值I1在角频率ω0=105rad/s时最小,最小值为1mA。试求电容C1以及电流I2和I3。

图7-22 题20图
解:由题意可判断出图7-22所示电路中虚线框内的实际并联谐振电路发生并联谐振,其谐振时的电路品质因数Q为
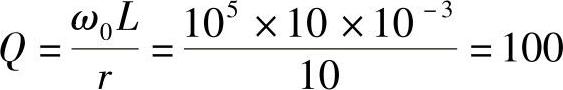
高Q条件下,谐振角频率ω0近似为
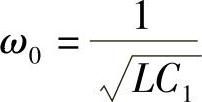
由此可得
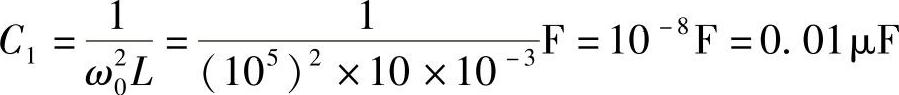
谐振时,有
I2=QI1=100×1mA=100mA
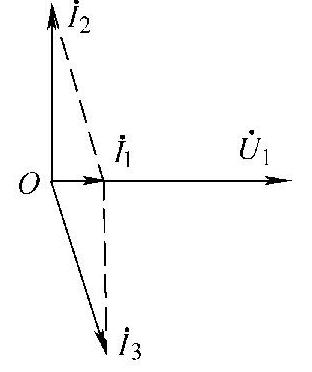
图7-23 题20解图
假设虚线框内实际并联谐振电路的端口电压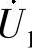 如图7-22所示,则由图7-23所示谐振时相量关系图可得
如图7-22所示,则由图7-23所示谐振时相量关系图可得

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




