电路谐振特性及应用研究

在含有动态元件的正弦稳态电路中，由于动态元件的容抗和感抗均是频率的函数，因此当电路中激励源的频率变化时，电路的正弦稳态响应一般会有相应变化，这种变化关系称为电路的频率特性。电路的频率特性常用正弦稳态电路的网络函数H（jω）来描述，包括幅频特性和相频特性两方面。网络函数H（jω）取决于电路的结构和参数，它是电路自身特性的反映，可通过电路分析计算或实验方法获得。通过网络函数可方便地求出电路在任一给定频率正弦信号激励下的稳态响应，若正弦激励f（t）=Acos（ω₀t+θ）作用于网络函数为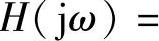的电路，其稳态响应可直接表示为

y（t）=A×H（jω₀）cos[ω₀t+θ+φ（ω₀）]

式中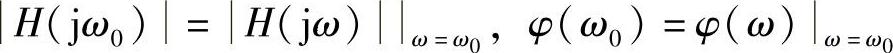

工程上，把电路幅频特性H（jω）从最大值H（jω）max到最大值的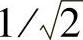的频率范围称为电路的通频带，也就是电路允许通过信号的频率范围。而把幅频特性值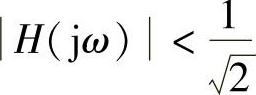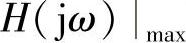对应的频率范围称为电路的阻带。把幅频特性值等于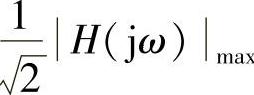时的频率称为电路的截止频率。一阶正弦稳态电路的截止频率恰好是其时间常数的倒数。

谐振是正弦交流电路在特定条件下产生的一种特殊物理现象，对于至少包含一个电感和一个电容元件的无源单口网络，在一定条件下，当其端口等效阻抗（或导纳）呈现纯电阻性时，即端口电压与端口电流同相，就称电路发生了谐振，或电路工作在谐振状态。谐振是谐振电路频率特性上的一个特殊工作点，有两种方法可使谐振电路达到谐振状态：一是调节激励信号的频率，使信号频率等于电路的谐振频率；二是改变电路元件的参数，使电路的固有谐振频率等于信号的频率。

谐振电路因其对信号频率具有优良选择性而被广泛应用于通信系统中。最简单的谐振电路为RLC串联谐振电路和RLC并联谐振电路，两种电路结构相互对偶，因此电路特性也完全对偶，对比关系如表7-1所示，学习中应注意对两者对照理解。(www.xing528.com)

表7-1 RLC串、并联谐振电路谐振特性对比

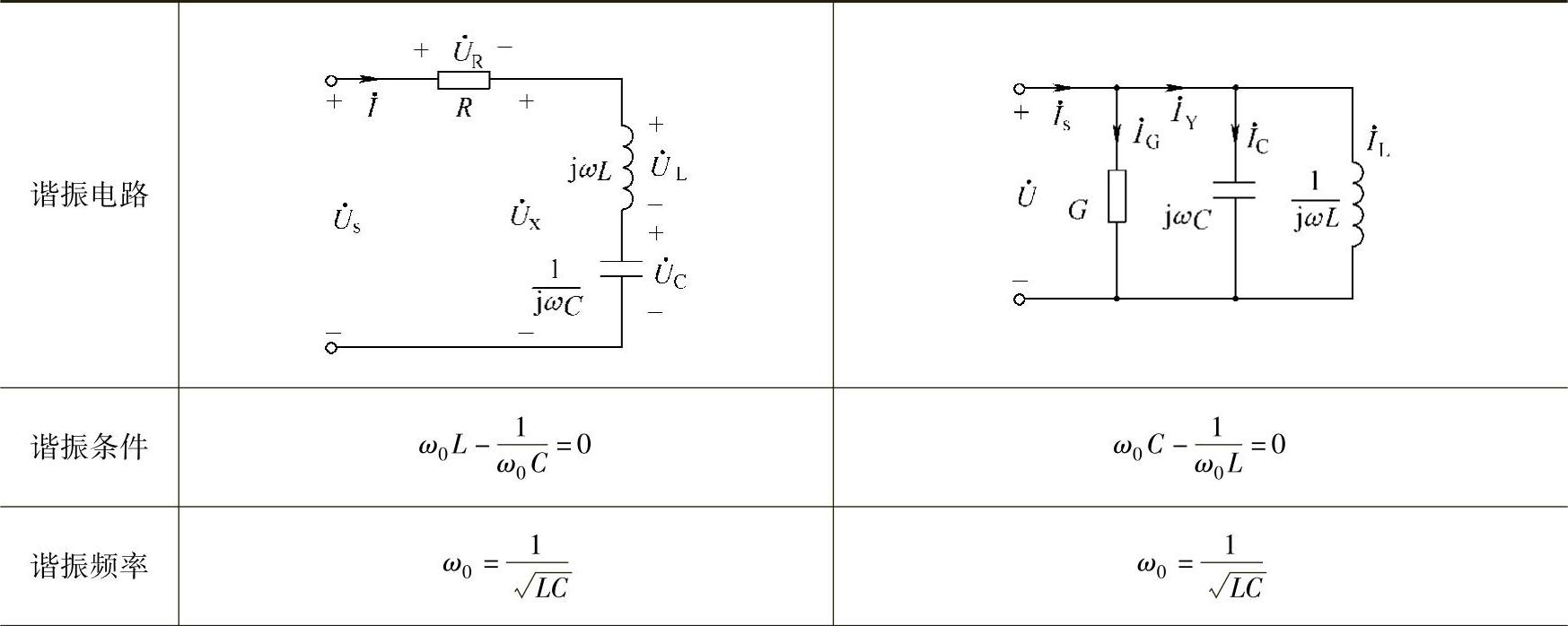
（续）