解析：无源单口电路电压电流关系优化后，给你看

1.已知正弦电流i（t）=30cos（1000t-30°）A。

（1）求该电流的幅值、角频率、频率、周期、初相和有效值。

（2）电流i（t）与下列各电流的相位差分别是多少？

i₁（t）=cos1000tA；i₂（t）=sin1000tA；i₃（t）=sin（1000t+45°）A

解：（1）电流i（t）的幅值I_m=30A，角频率ω=1000rad/s，频率f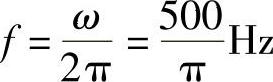，周期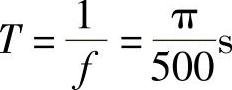，初相φ=-30°，有效值。

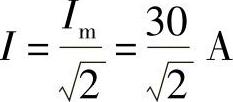（2）电流i（t）与电流i₁（t）的相位差为

θ=-30°-0°=-30°

电流i（t）滞后电流i₁（t）30°。

电流i₂（t）可表示为

i₂（t）=sin1000tA=cos（1000t-90°）A

电流i（t）与电流i₂（t）的相位差为

θ=-30°-（-90°）=60°

电流i（t）超前电流i₂（t）60°。

电流i₃（t）可表示为

i₃（t）=sin（1000t+45°）A=cos（1000t-90°+45°）A=cos（100t-45°）A

电流i（t）与电流i₃（t）的相位差为

θ=-30°-（-45）°=15°

电流i（t）超前电流i₃（t）15°。

2.请把下列复数表示为直角坐标形式：

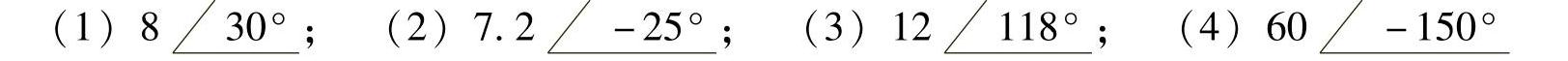
解：

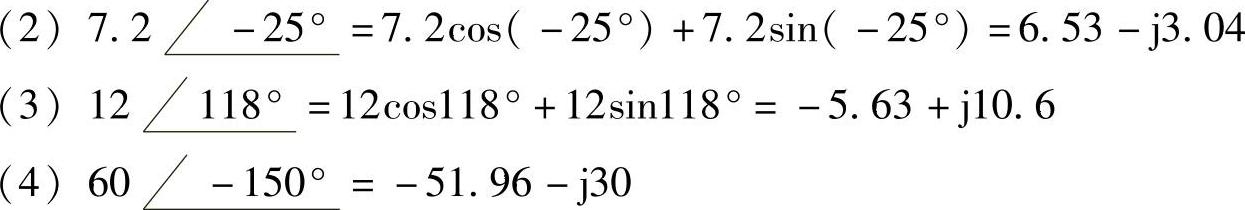
3.请把下列复数表示为极坐标形式：

（1）8+j5 （2）4-j4 （3）-6.4-j3.2 （4）-3+j4

解：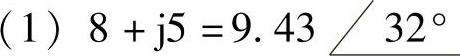

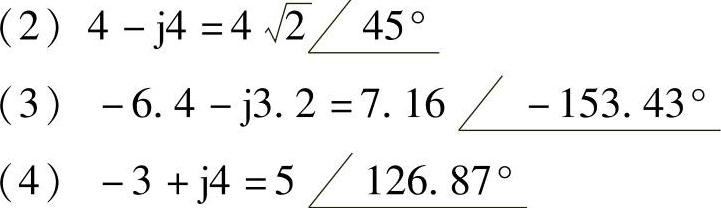
4.复数计算

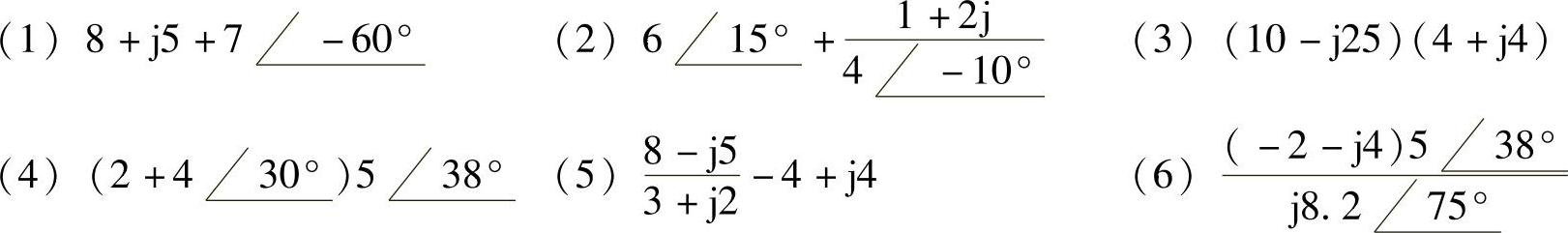
解：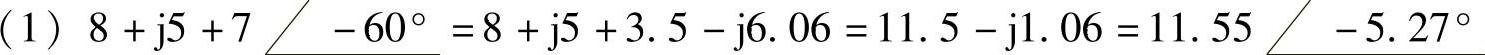

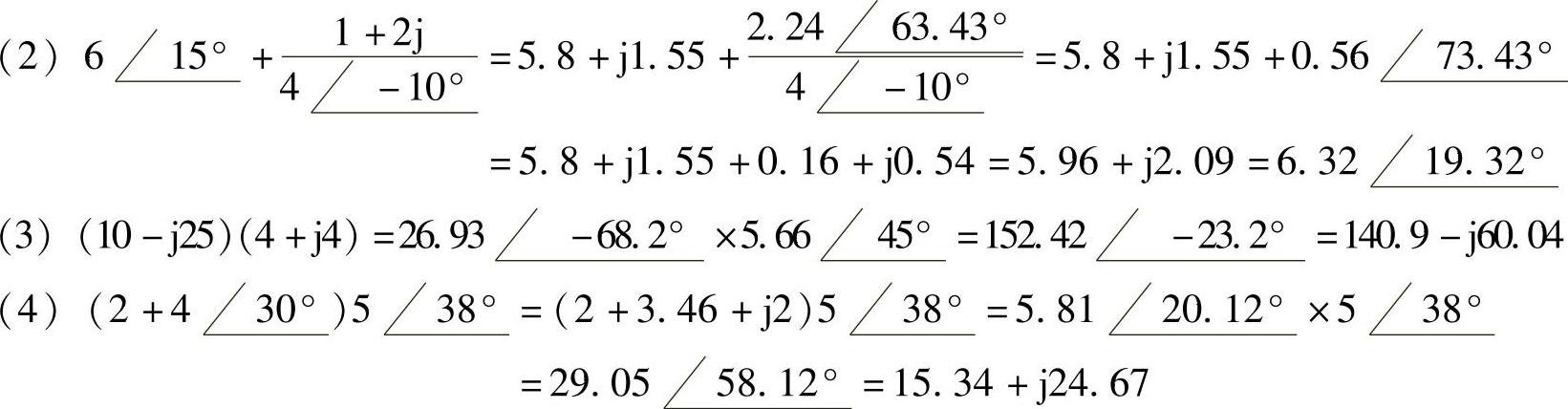
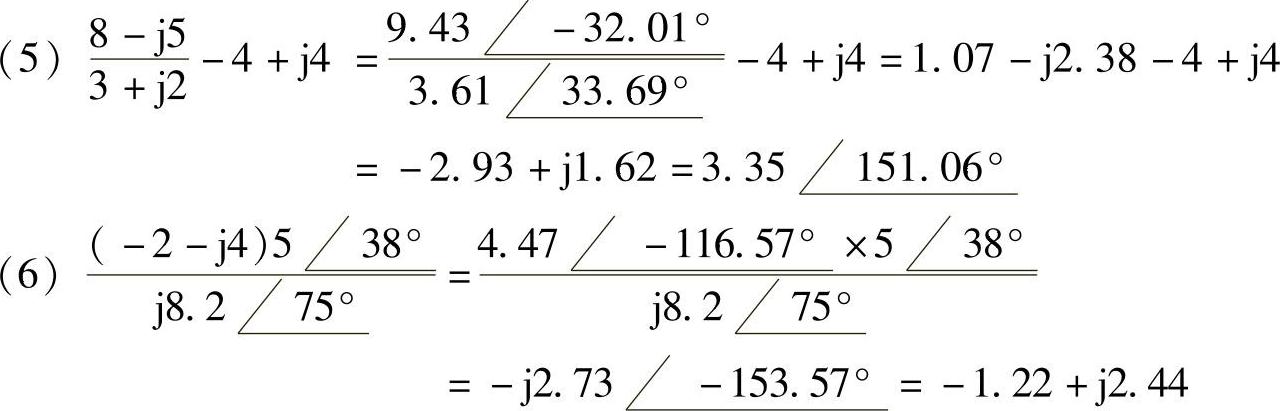
5.求下列正弦电压对应的相量，并画出相量图：

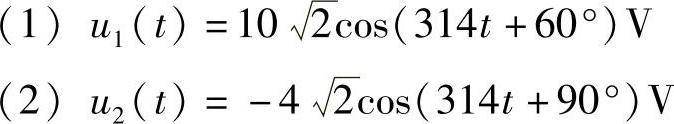
解：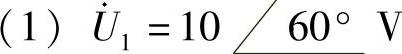

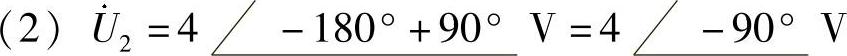
相量图如图6-11所示。

6.已知电流相量，且f=50Hz，写出其对应的正弦电流表达式。

解：ω=2πf=100πrad/s

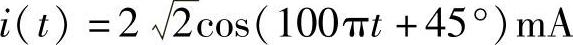
7.用相量变换的方法求以下正弦函数的和：

（1）4cos2t+3sin2t

（2）-6cos（4t+75°）+4cos（4t+35°）

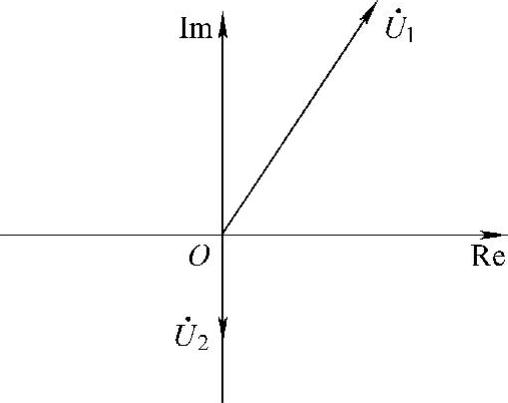
图6-11 题5解图

解：（1）对正弦函数做相量变换，4cos2t对应相量为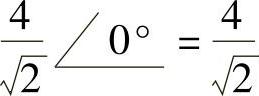，3sin2t=3cos（2t-90°）对应相量为，在相量域进行相量的求和运算，即

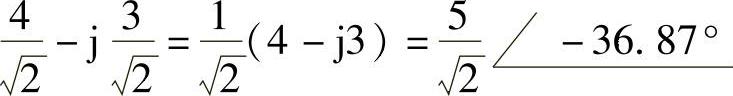
做相量反变换，得5cos（2t-36.87°），则

4cos2t+3sin2t=5cos（2t-36.87°）

（2）对正弦函数做相量变换，有

-6cos（4t+75°）对应的相量为，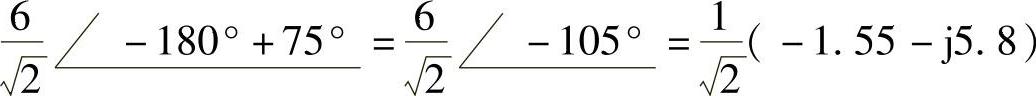

4cos（4t+35°）对应的相量为，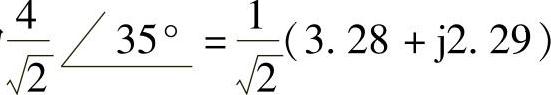

两个相量之和为

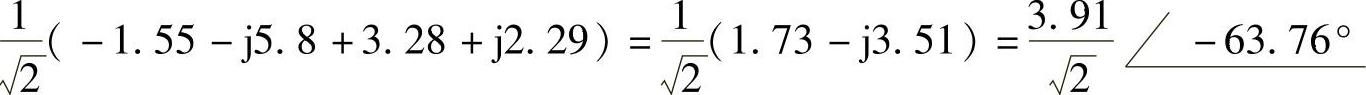
做相量反变换，得 3.91cos（4t-63.76°）

求得 -6cos（4t+75°）+4cos（4t+35°）=3.91cos（4t-63.76°）

8.电路如图6-12所示，已知电流i（t）=10cos10tA。

（1）请画出相量电路。

（2）用相量法求电压u（t）。

（3）求端口电压相量与电流相量的比值，即。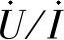

解：（1）相量电路如图6-13所示。

（2）电流i（t）对应的相量为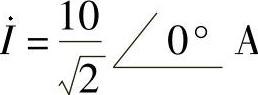A，根据图6-13可得

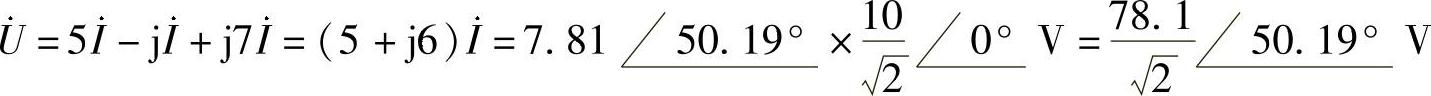
相量反变换得 u（t）=78.1cos（10t+50.19°）V

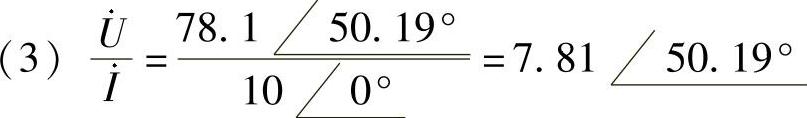
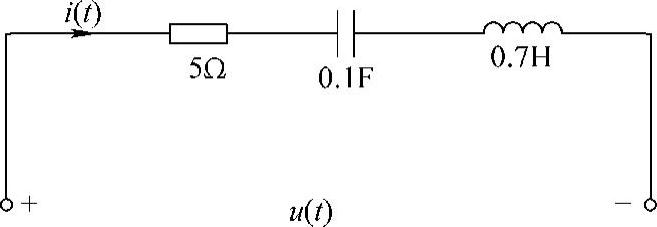
图6-12 题8图

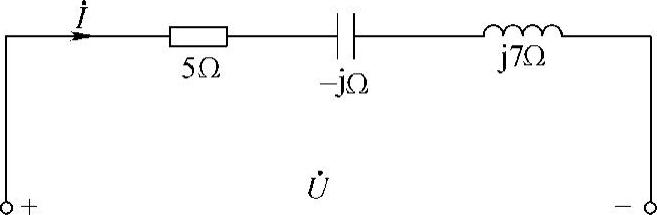
图6-13 题8解图

9.无源单口电路如图6-14所示，若端口电压与电流分别为以下几种情况：

（1）u（t）=10cos（10t+45°）V，i（t）=2cos（10t-15°）A。

（2）u（t）=10cos（10t+50°）V，i（t）=2cos（10t+140°）A。

（3）u（t）=10sin100tV，i（t）=2cos100tA。

（4）u（t）=-10cos10tV，i（t）=-2sin10tA。求各种情况下的端口等效阻抗Z、构成电路N的元件参数、端口电压与电流的相位差，并指明哪个电量超前。

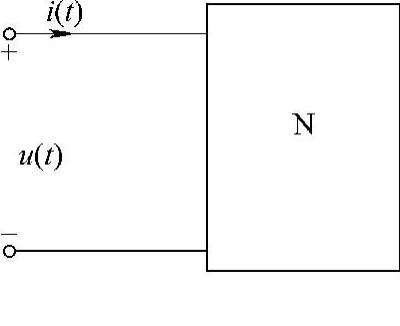
图6-14 题9图

解：（1）端口电压相量和电流相量分别为，。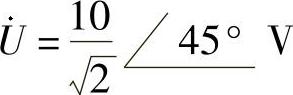

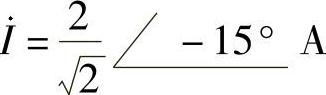端口等效阻抗为

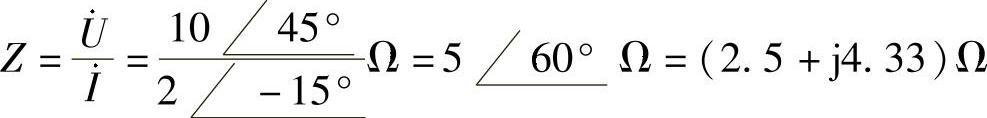
电路N呈感性，可由电阻和电感串联构成，根据Z=R+jωL=（2.5+j4.33）Ω，得

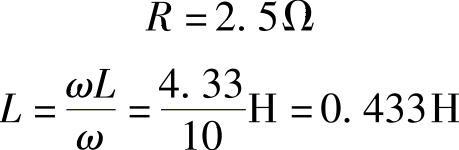
端口电压与电流的相位差为θ_Z=60°，电压超前电流。

（2）端口电压相量和电流相量分别为，。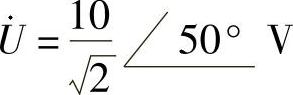

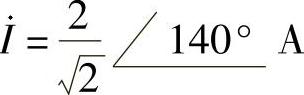端口等效阻抗为

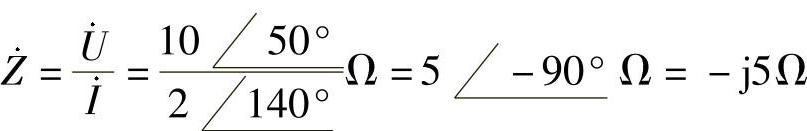
电路N为纯电容，即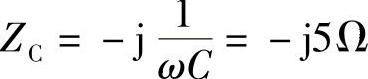，电容值为

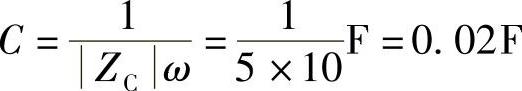
端口电压与电流的相位差为θ_Z=-90°，电流超前电压。

（3）端口电压相量和电流相量分别为，。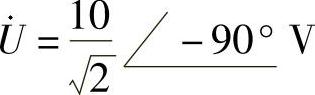

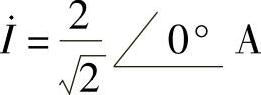端口等效阻抗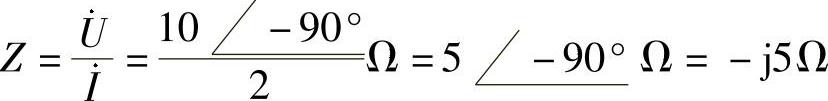

电路N为纯电容电路，电容值为

C=0.02F=2mF

端口电压与电流的相位差为θ_z=-90°，电流超前电压。

（4）端口电压相量和电流相量分别为，。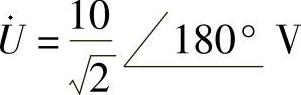

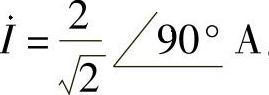端口等效阻抗为

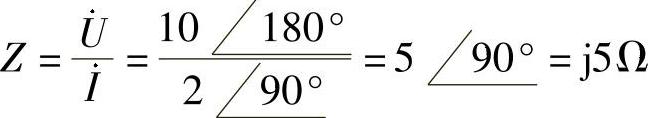
电路N为纯电感，即Z=jωL=j5Ω，有

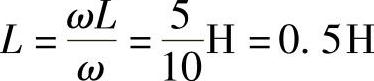
端口电压与电流的相位差θ_Z=90°，电压超前电流。

10.判断以下无源电路的结果是否合理，若认为不合理，请给予修正：

（1）RC电路：Z=（5+j2）Ω

（2）RL电路：Z=（4-j7）Ω

（3）LC电路：Z=（2-j3）Ω

（4）RLC电路：Z=（2+j4）Ω

（5）已知某电路的端口等效阻抗，端口电压为u（t）=300cos（10t+45°）V，在端口电压与电流参考方向关联的情况下，有

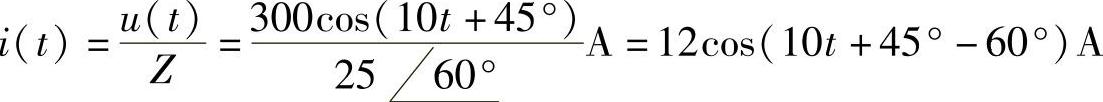
分析要点：此题的关键是要掌握阻抗形式与阻抗性质之间的关系。容性阻抗虚部为负，或者说，阻抗角在第4象限；感性阻抗虚部为正；反由储能元件构成的电路阻抗无实部；由电阻、电容、电感组成的电路阻抗角在第1或4象限。

解：（1）不合理。修正为Z=（5-j2）Ω。

（2）不合理。修正为Z=（4+j7）Ω。

（3）不合理。修正为Z=-j3Ω。

（4）合理。

（5）不合理。修正为

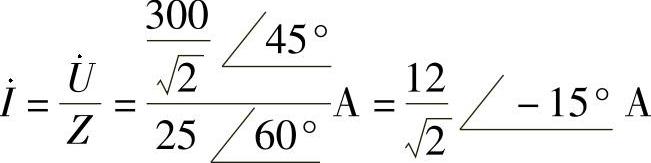
相量反变换，得 i（t）=12cos（10t-15°）A。

11.指出下列各式哪些是对的，哪些是错的：

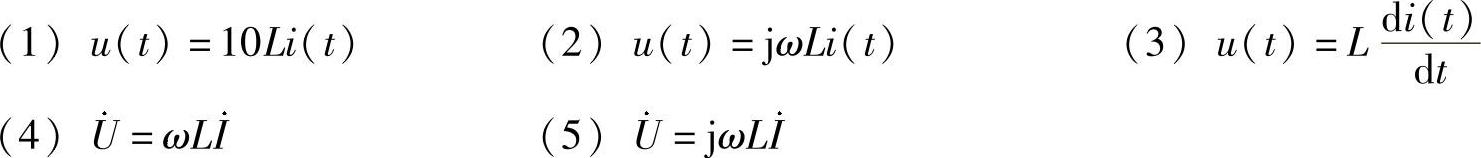
解：（1）错。修改为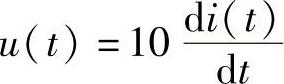

（2）错。修改为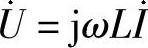

（3）对。

（4）错。修改为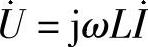

（5）对。

12.试求：（1）200μF电容在50Hz和50kHz频率的阻抗值。

（2）1.4H电感在50Hz和50kHz频率的阻抗值。

解：（1）在50Hz频率时，阻抗为

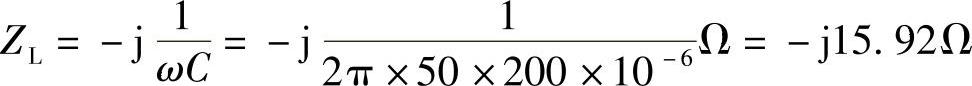
在50kHz频率时，阻抗为

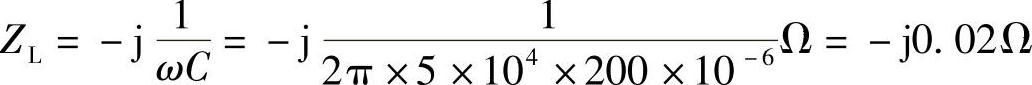
（2）在50Hz频率时，阻抗为

Z_C=jωL=j2π×50×1.4Ω=j439.82Ω

在50kHz频率时，阻抗为

Z_C=jωL=j2π×5×10⁴×1.4Ω=j439.82kΩ

题意启示：电容、电感的阻值随频率变化。频率低，感抗小，容抗大。频率高，感抗大，容抗小。

13.求图6-15所示电路在ω=50rad/s的输入阻抗Z_i。

解：画相量电路，如图6-16所示。

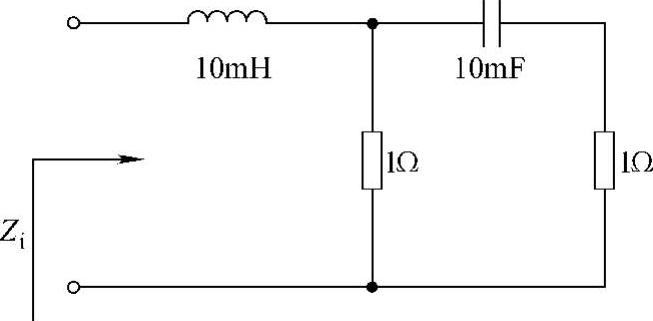
图6-15 题13图

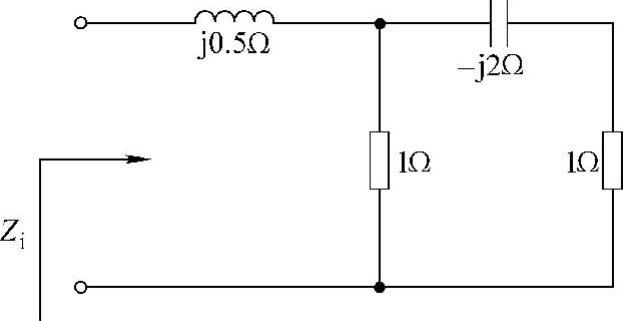
图6-16 题13解图

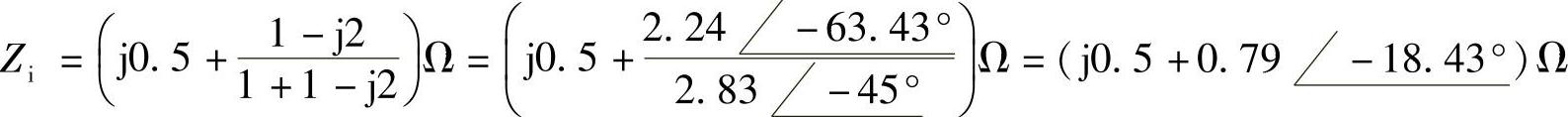
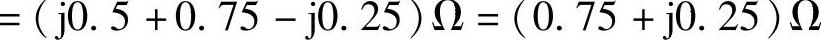
14.电路如图6-17所示，使u₀（t）=u_s（t）的角频率是 （4）

(1)Orad/s (2)lrad/s (3)4rad/s

(4)∞rad/s (5)以上选择都不对

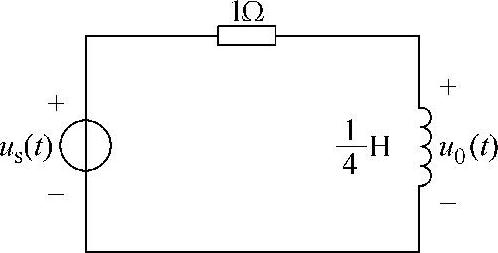
图6-17 题14图

15.图6-18所示电路中的电压源u_s（t）=5cos（2t）V，求电压u₀（t）。

解：画相量电路，如图6-19所示。由分压公式得

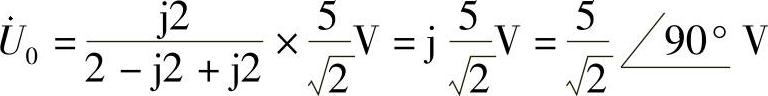
做相量反变换，得 u₀（t）=5cos（2t+90°）V

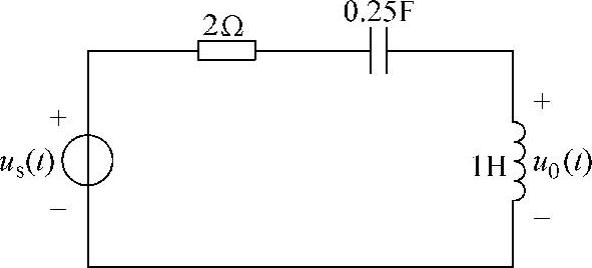
图6-18 题15图

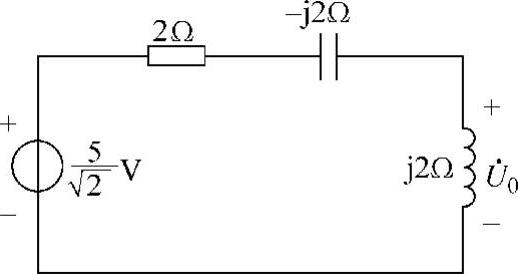
图6-19 题15解图

16.求图6-20所示各电路的电流i（t）和电压u（t）。

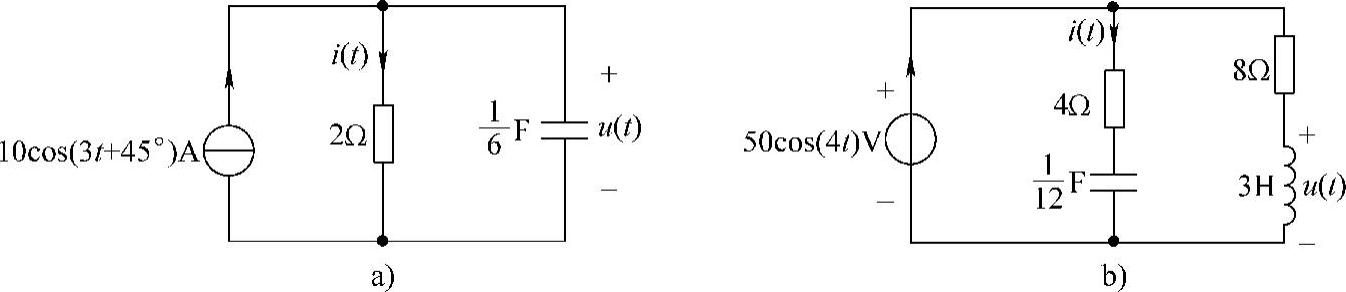
图6-20 题16图

解：（1）画图6-20a的相量电路，如图6-21所示。根据分流公式，得

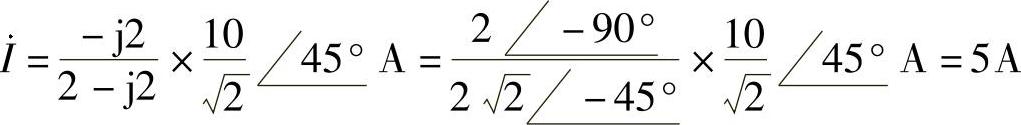
则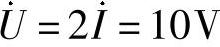

做相量反变换，得

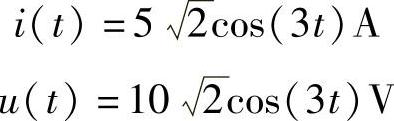
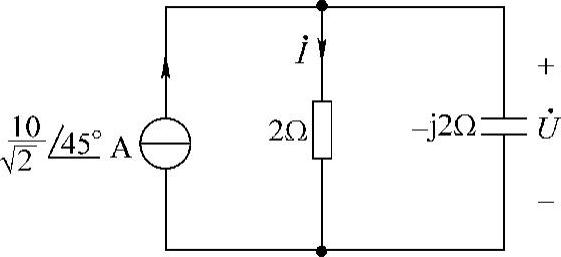
图6-21 题16解图

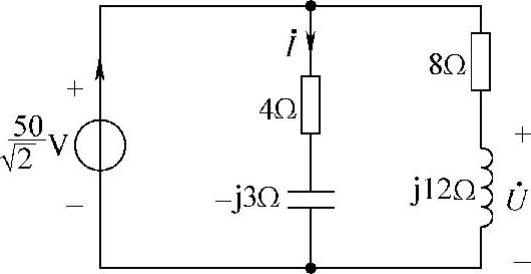
图6-22 题16解图

（2）画图6-20b的相量电路，如图6-22所示。利用相量形式的欧姆定律，得

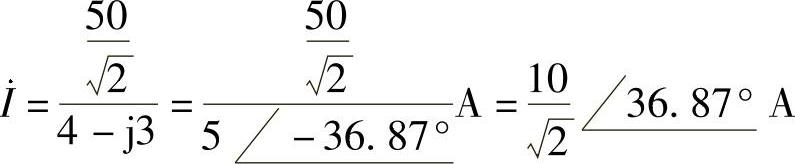
利用分压公式可得

做相量反变换，得

i（t）=10cos（4t+36.87°）A

u（t）=41.61cos（4t+33.69°）V

17.求图6-23所示各电路的端口等效阻抗和导纳。

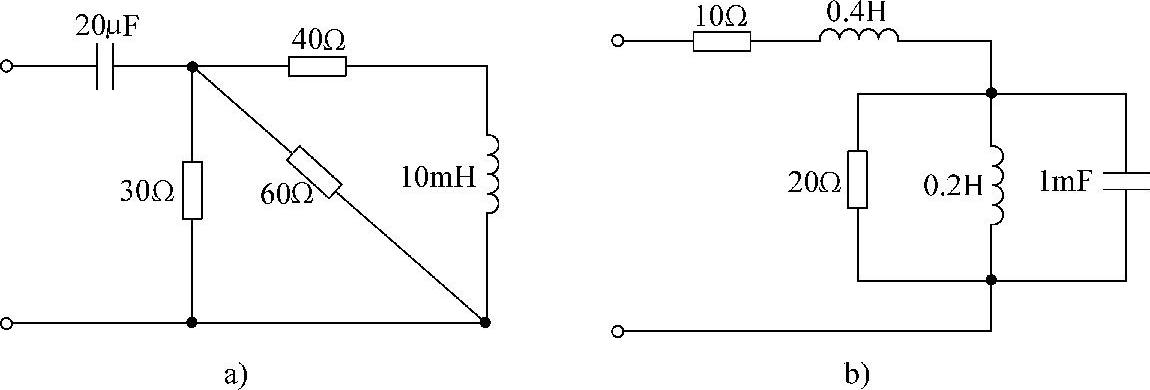
图6-23 题17图

a）ω=10³rad/s b）ω=50rad/s

解：图6-23a所示电路的相量电路如图6-24a所示。利用阻抗串并、联化简公式，得端口等效阻抗为

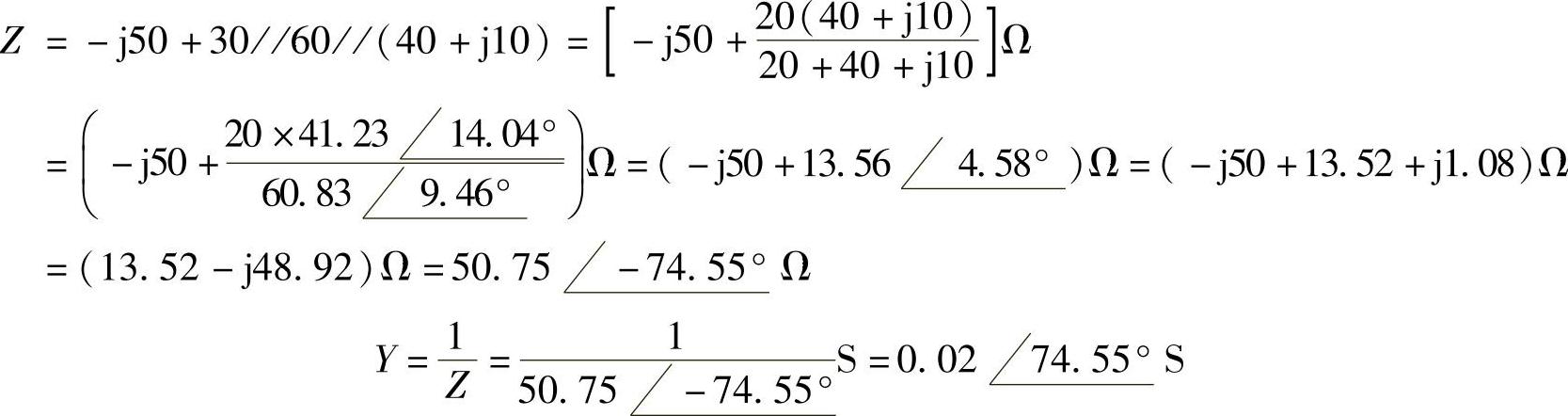
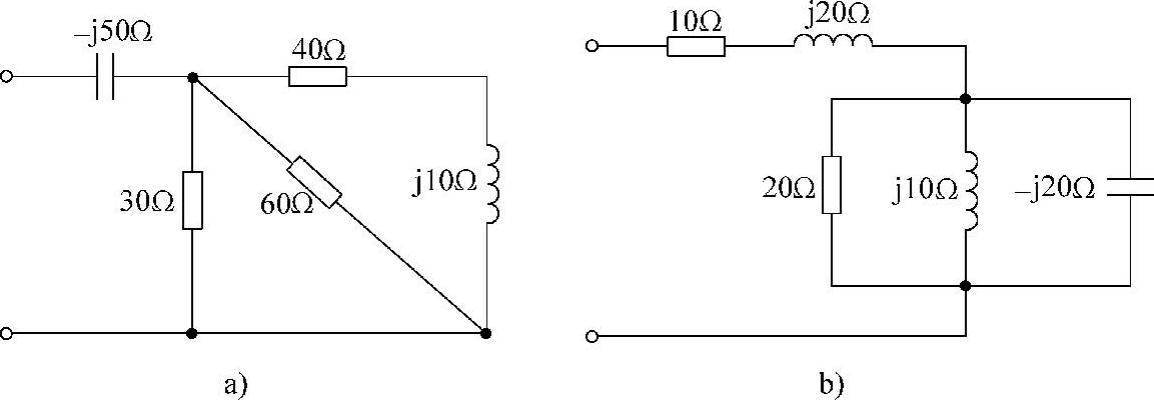
图6-24 题17解图

图6-23b所示电路的相量电路如图6-24b所示。端口等效阻抗为

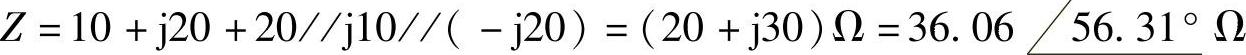
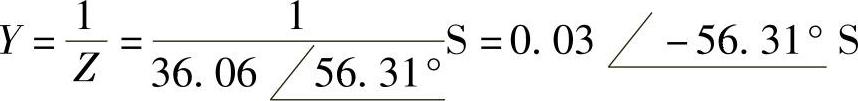
18.电路如图6-25所示，求在以下两种情况下的电流i（t）。

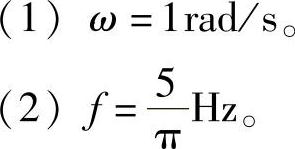
解：（1）当ω=1rad/s时，相量电路如图6-26所示。由图可得

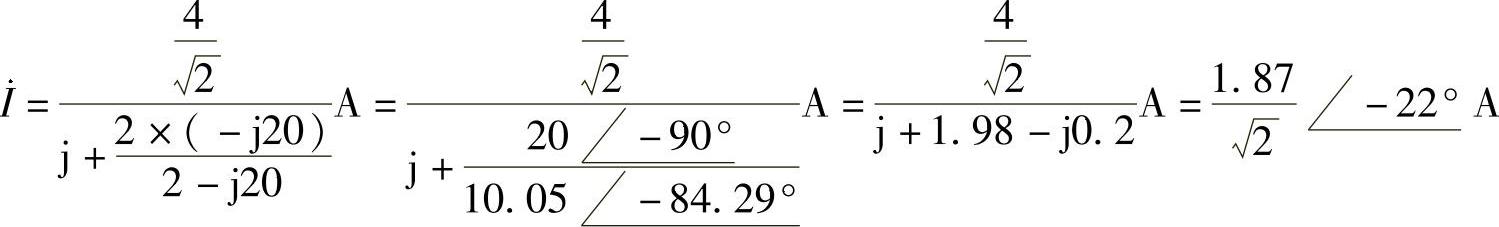
做相量反变换，得i（t）=1.87cos（t-22°）A

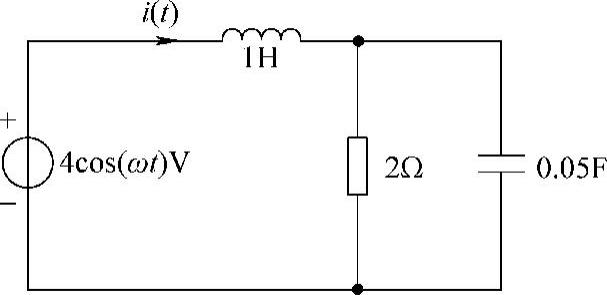
图6-25 题18图

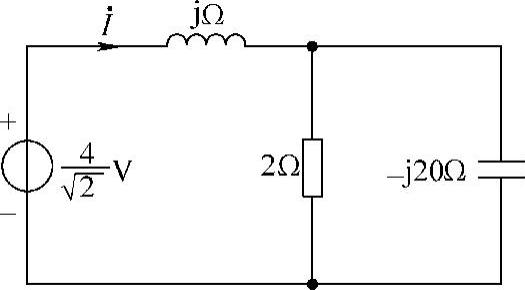
图6-26 题18解图

（2）当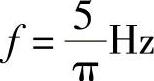，即ω=10rad/s时，相量电路如图6-27所示。由图可得

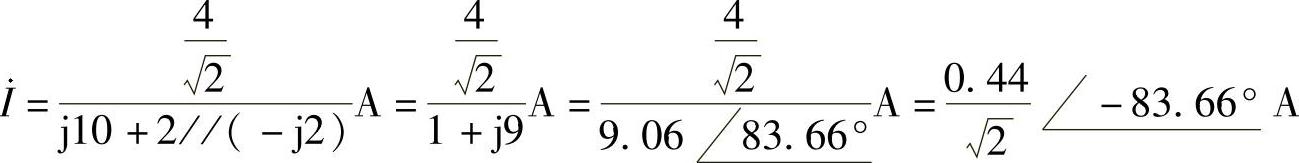
做相量反变换，得 i（t）=0.44cos（10t-83.66°）A

19.电路如图6-28所示，求电压。

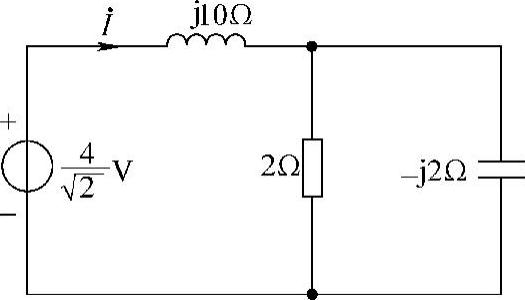
图6-27 题18解图

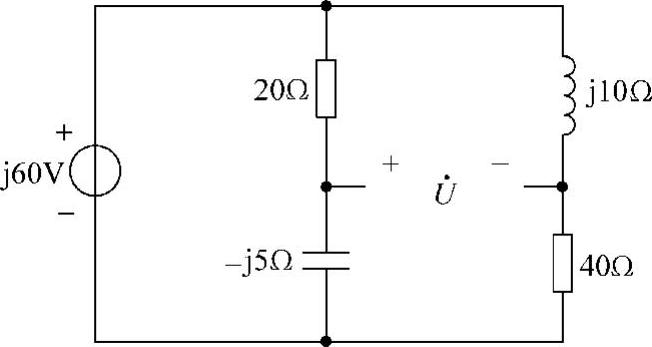
图6-28 题19图

解：设电压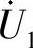和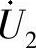如图6-29所示。利用分压公式，得

20.选择题。图6-30所示电路中的电压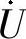是（3）。

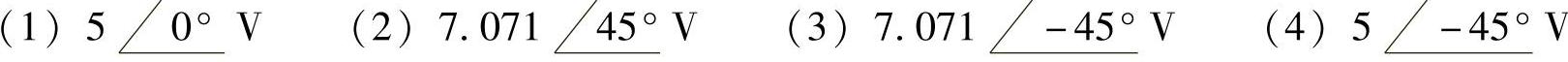
图6-29 题19解图

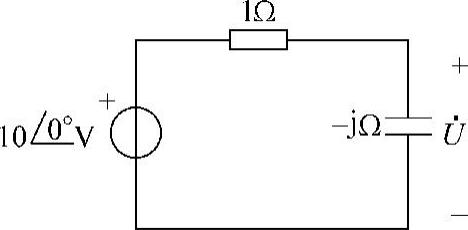
图6-30 题20图

21.求图6-31所示电路中的u（t）和i（t）。

解：画相量电路，如图6-32所示。电感与电阻并联的等效阻抗为

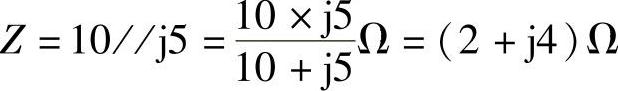
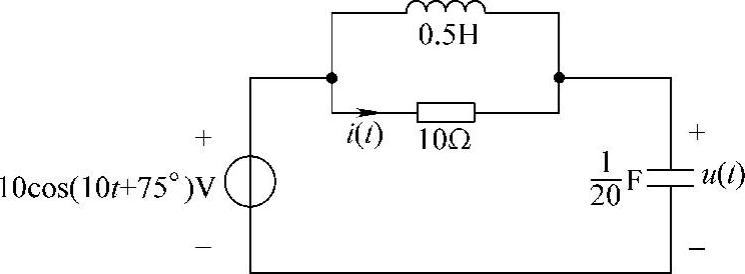
图6-31 题21图

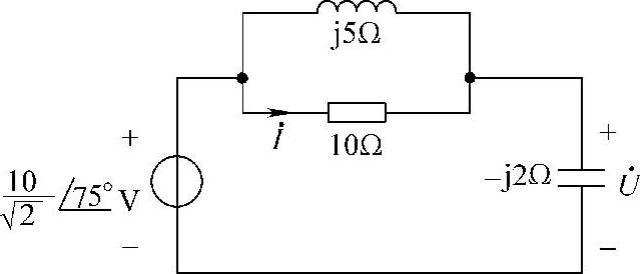
图6-32 题21解图

利用分压公式得

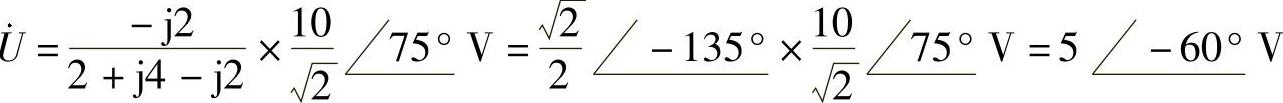
电流相量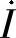为

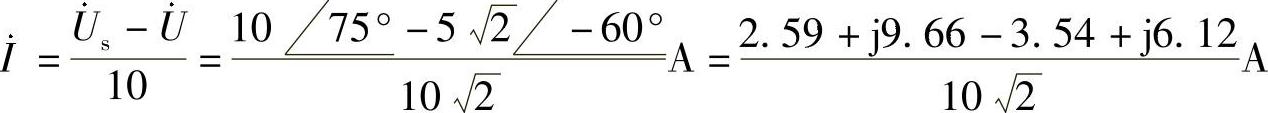
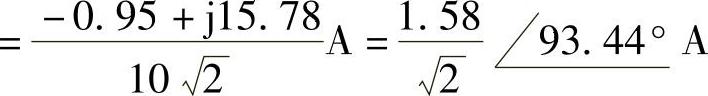
相量反变换，得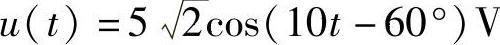

i（t）=1.58cos（10t+93.44°）A

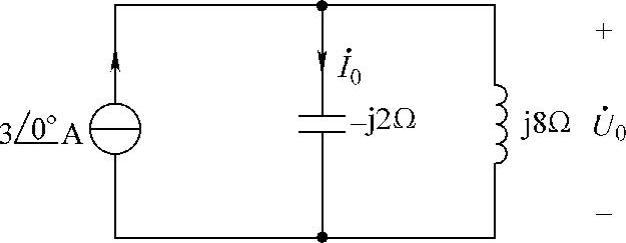
图6-33 题22、23图

22.选择题。图6-33所示电路中的电流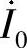是（1）。

23.选择题。在图6-33所示电路中，电压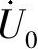的有效值为（3）。

（1）-4.8V （2）-8V （3）8V （4）4.8V

24.选择题。图6-34所示电路ab端口的戴维南等效阻抗Z_ab为（3）。

（1）1Ω （2）（0.5-j0.5）Ω （3）（0.5+j0.5）Ω

（4）（1+j2）Ω （5）（1-j2）Ω

25.选择题。图6-34所示电路ab端口的开路电压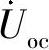为（1）。

26.选择题。电路如图6-35所示，ab端口的诺顿等效电流为（4）。

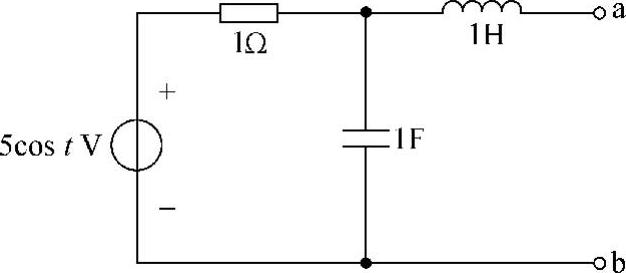
图6-34 题24、25图

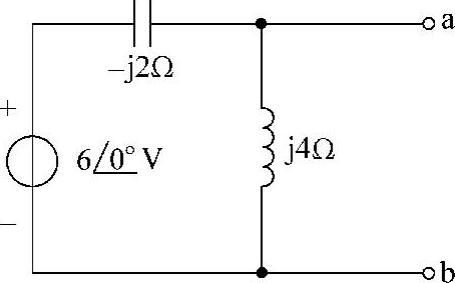
图6-35 题26图

27.电路如图6-36所示，求电流i₀（t）。

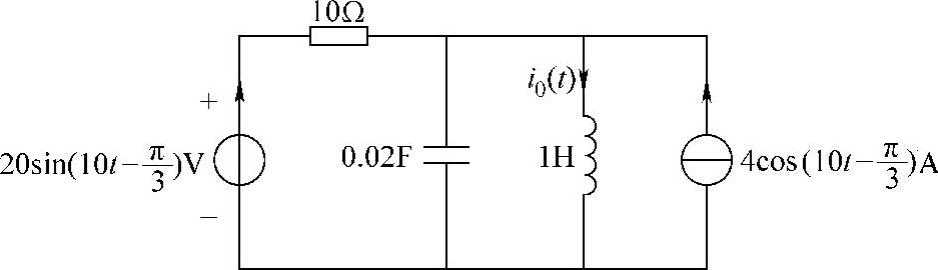
图6-36 题27图

解：原电路的相量电路模型如图6-37所示。列结点电压方程

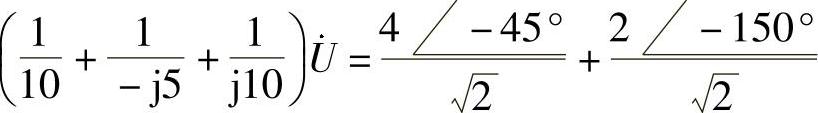
则有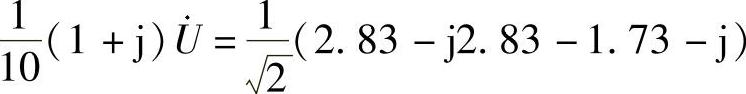

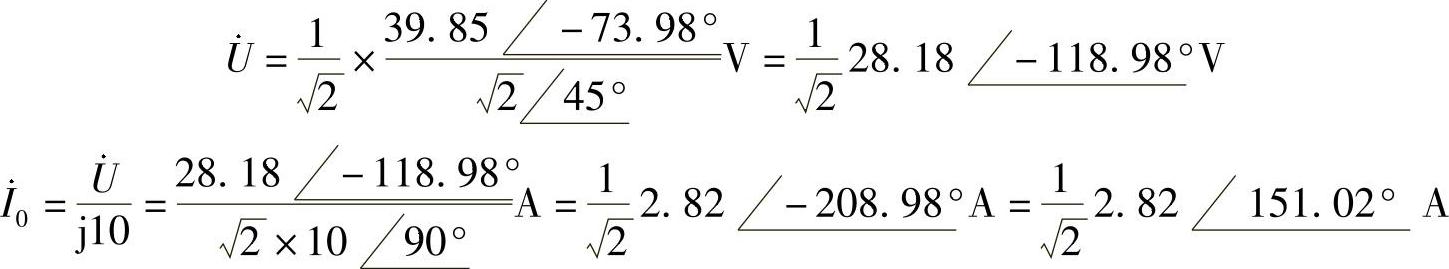
做相量反变换，得

i₀（t）=2.82cos（10t+151.02°）A

注意：为确保初相取值的唯一性，规定初相的取值范围为-180°≤φ≤180°。这就是说，当初相在一、二象限时取正角，在三、四象限时取负角。此题电流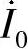的初相-208.98°超出了取值范围，且在第二象限，故取正角，为φ=360°-208.98°=151.02°。

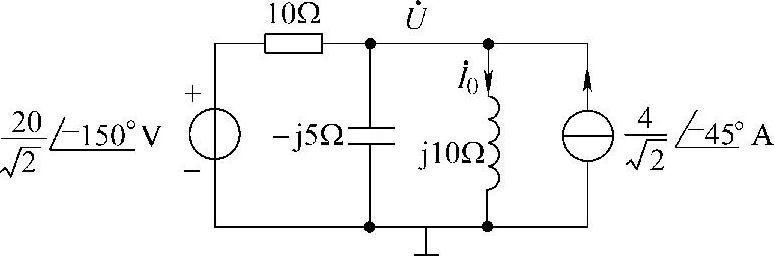
图6-37 题27解图

28.请列出图6-38所示电路的结点电压方程。

解：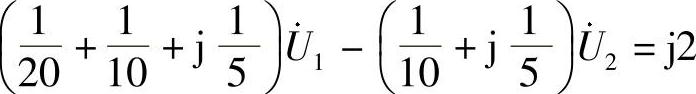

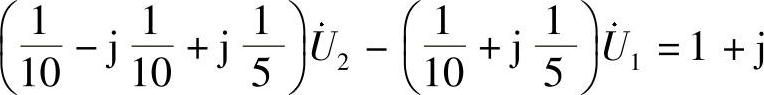
29.请列出图6-39所示电路的结点电压方程。

解：设参考结点及结点电压如图6-40所示。结点电压方程为

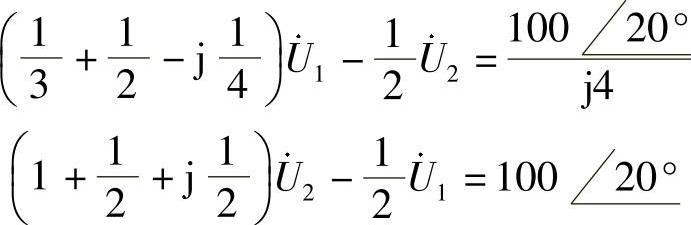
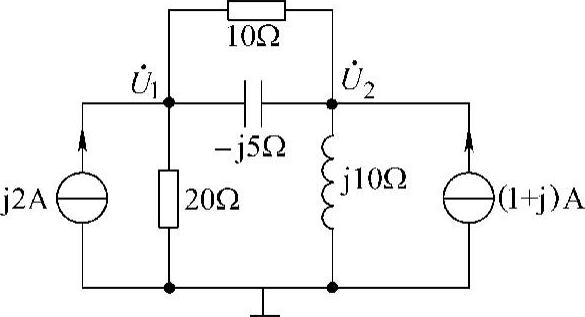
图6-38 题28图

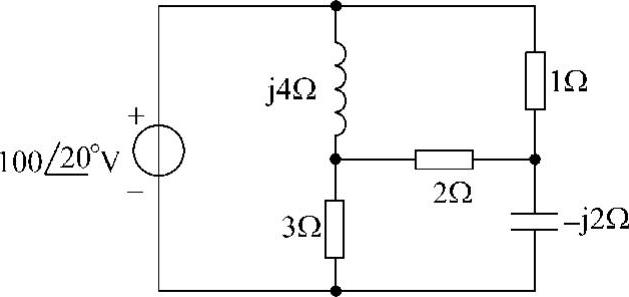
图6-39 题29图

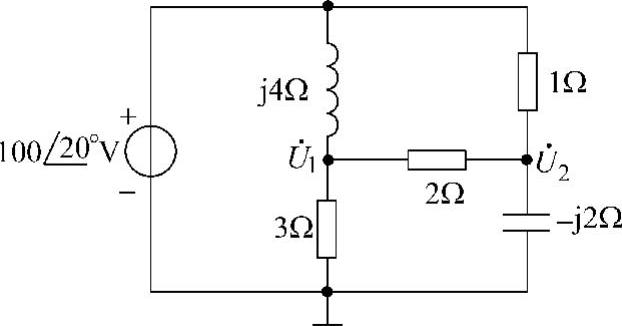
图6-40 题29解图

30.试用网孔法求图6-41所示电路的电流和。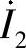

解：设网孔电流方向，如图6-42所示。图中两个网孔电流方程分别为

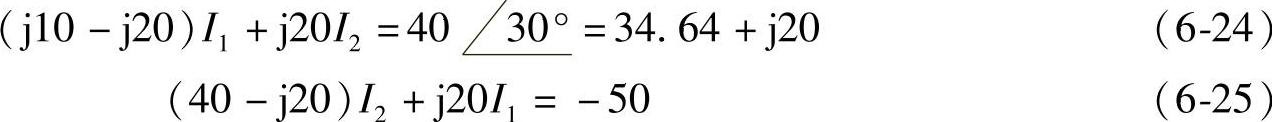
式（6-24）×2+式（6-25），得

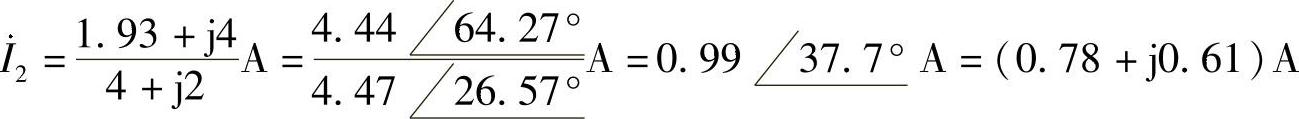
把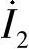代入式（6-24），有(https://www.xing528.com)

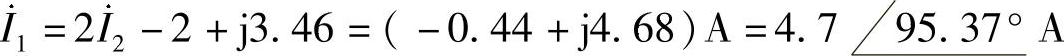
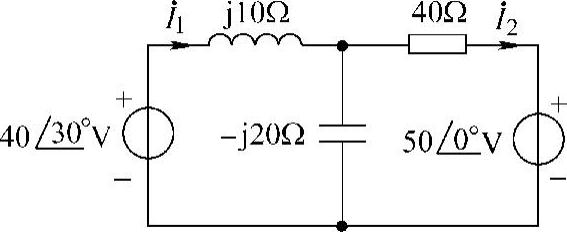
图6-41 题30图

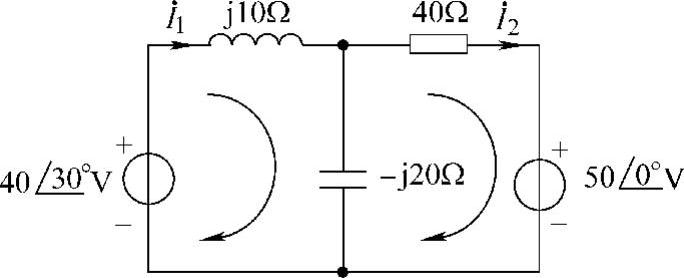
图6-42 题30解图

31.试用网孔法计算图6-43所示电路中的电压。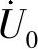

要点：在三个网孔电流中，两个网孔电流为已知的电流源电流，因此，只需列一个方程，求一个网孔电流。

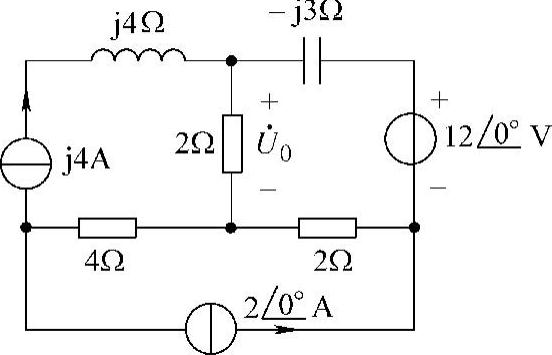
图6-43 题31图

解：设网孔电流及参考方向，如图6-44所示。右上角网孔电流方程为

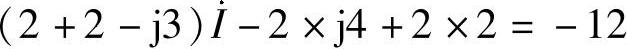
得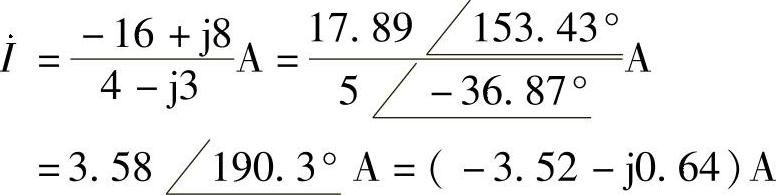

则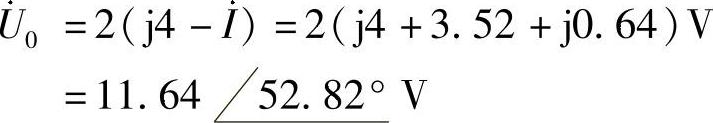

32.电路如图6-45所示，求电压u₀（t）。

当电路中独立源的频率各不相同时，必须用叠加法。该题就属于这种情况。

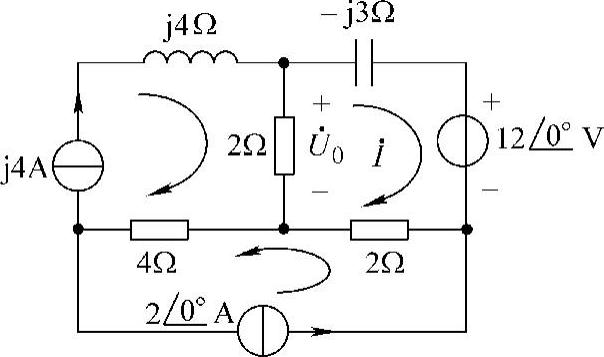
图6-44 题31解图

解：用叠加法。

（1）10V直流电压源单独作用，其余电源置零。在直流电路中，电容开路，电感短路，等效电路如图6-46a所示。由图可知

U₀=10V

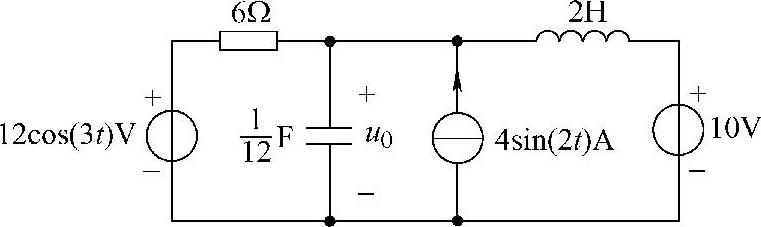
图6-45 题32图

（2）12cos（3t）V正弦电压源单独作用，等效电路如图6-46b所示。利用分压公式得

则 u₁（t）=10.71cos（3t-26.57°）V

（3）4sin（2t）A正弦电流源单独作用，等效电路如图6-46c所示。电流源端口的等效导纳为

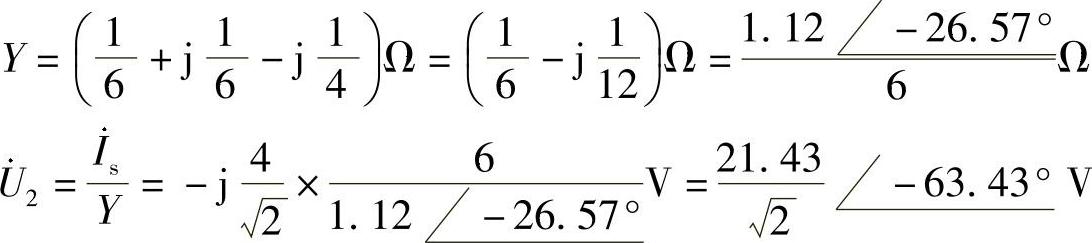
则 u₂（t）=21.43cos（2t-63.43°）V

时域叠加，得

u（t）=U₀+u₁（t）+u₂（t）=[10+10.71cos（3t-26.57°）+21.43cos（2t-63.43°）]V

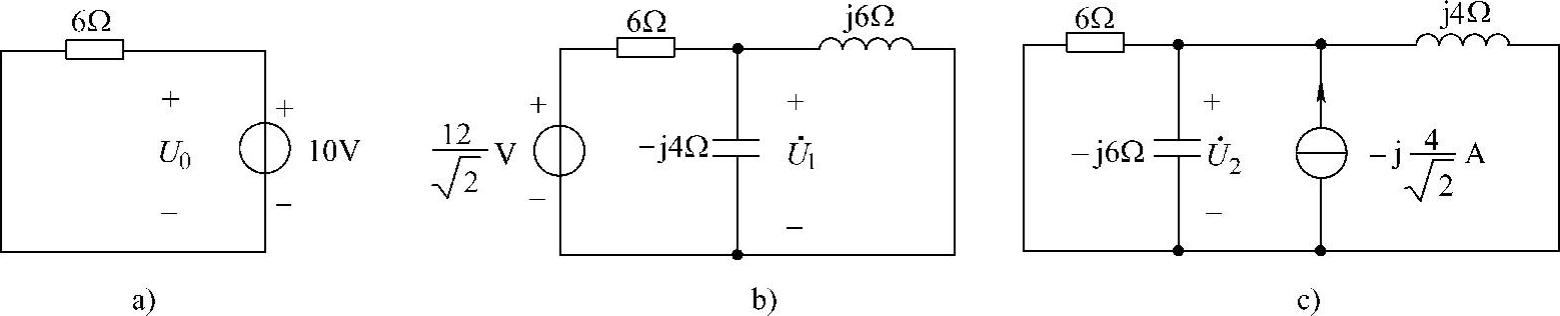
图6-46 题32解图

33.选择题。已知某电路在负载端口的戴维南等效阻抗是（80+j55）Ω，为使负载阻抗获得最大功率，负载阻抗必须是（3）。

（1）（-80+j55）Ω （2）（-80-j55）Ω （3）（80-j55）Ω （4）（80+j55）Ω

34.电路如图6-47所示，求电流i（t）。

解：相量电路如图6-48所示。利用分流公式可得

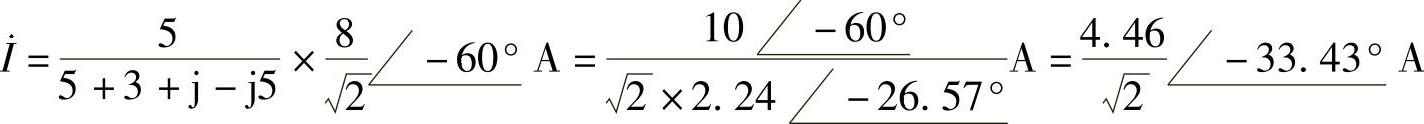
得 i（t）=4.46cos（200t-33.43°）A

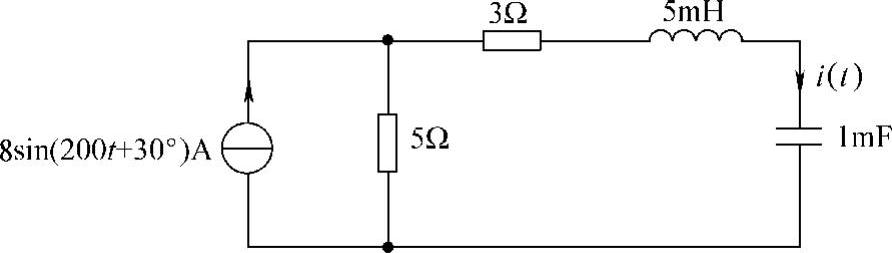
图6-47 题34图

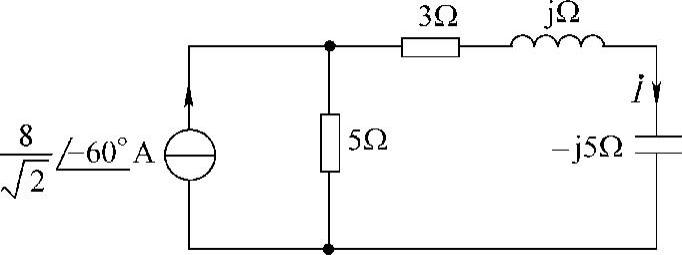
图6-48 题34解图

35.已知某正弦稳态电路的端口电压为u（t）=80cos（10t+20°）V，端口电流为i（t）=15sin（10t+60°）A，求该电路的平均功率。

解：端口电压、电流相量分别为，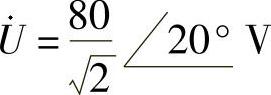

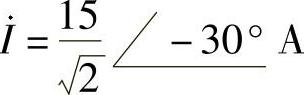
该电路的平均功率为

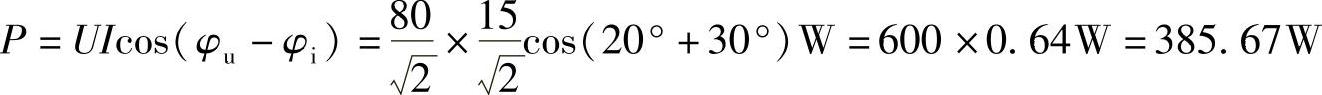
36.已知电流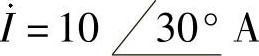流过导纳Y=0.0522°S，求导纳的损耗功率。

解：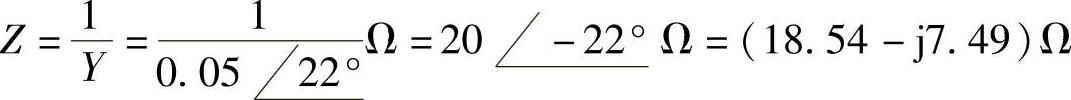

则 P=Re[Z]I²=RI²=18.54×10²W=1854W。

37.求图6-49所示各电路ab端口的戴维南等效电路。

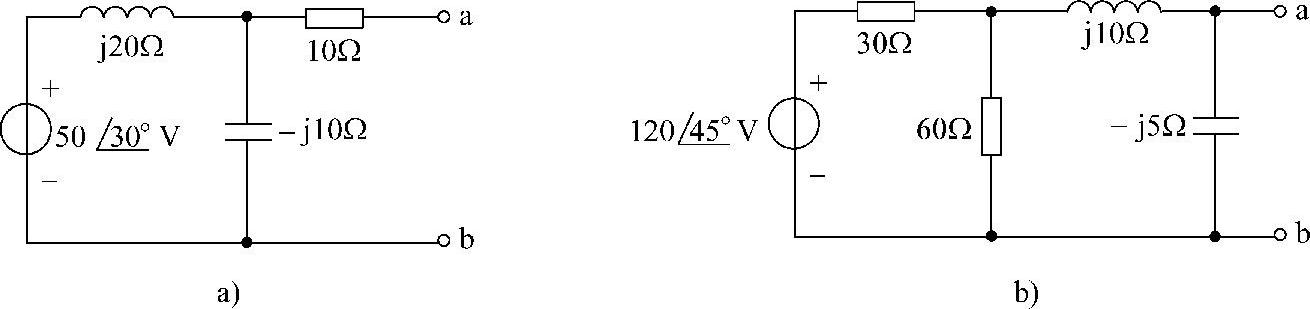
图6-49 题37图

解：（1）求图6-49a所示电路的戴维南等效电路。

端口开路电压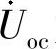为

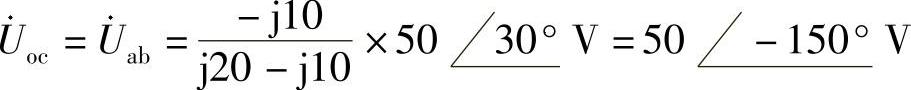
图6-49a所示电路的ab端口等效阻抗为

Z₀=[j20//（-j10）+10]Ω=（10-j20）Ω

等效电路如图6-50a所示。

（2）求图6-49b所示电路的戴维南等效电路。

化简图6-49b所示电路，如图6-50b所示。端口开路电压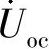为

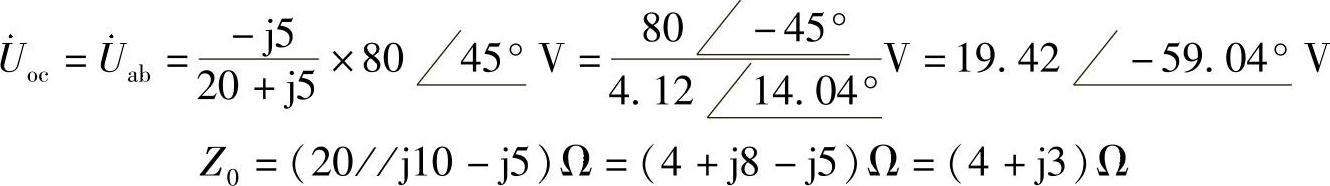
等效电路如图6-50c所示。

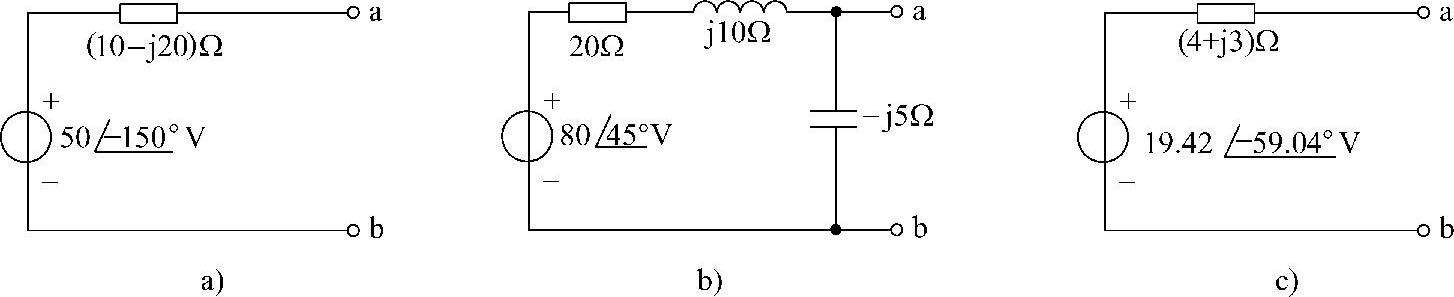
图6-50 题37解图

38.电路如图6-51所示，求各元件的平均功率。

思路：先求各支路电流，再通过支路电流求电阻、电源的平均功率。由概念可知电容和电感的平均功率为零。

解：设网孔电流，如图6-52所示。列网孔电流方程，求和。

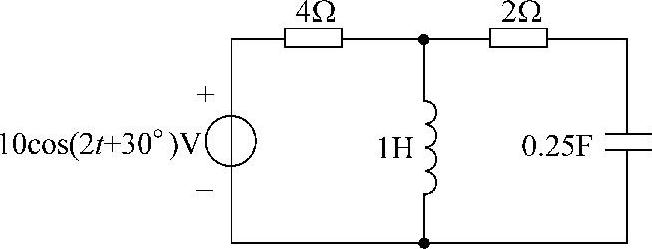
图6-51 题38图

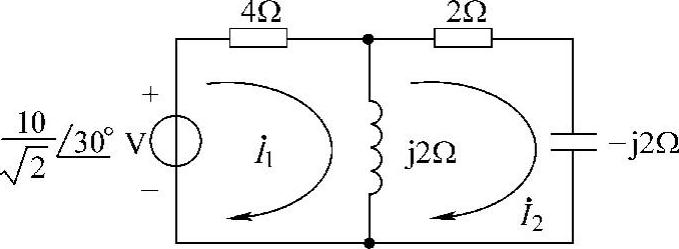
图6-52 题38解图

网孔1方程

网孔2方程

式（6-27）化简为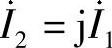，代入式（6-26），得

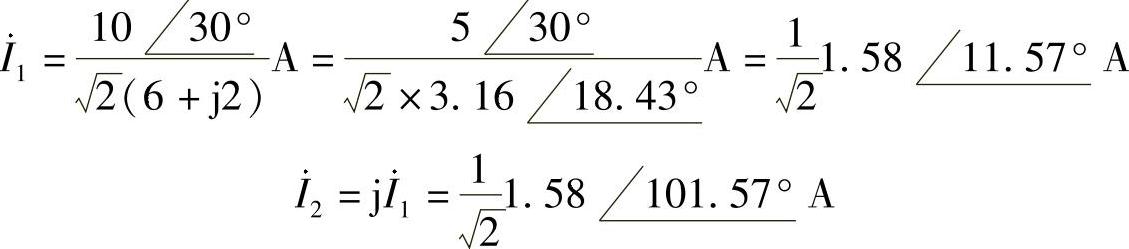
4Ω电阻的平均功率为 P₁=4I₁²=2×1.58²W=5W

2Ω电阻的平均功率为 P₂=2I₂²=1.58²W=2.5W

根据功率守恒定律可知，电压源的平均功率为

P_s=-（P₁+P₂）=-（5+2.5）W=-7.5W

或者直接计算得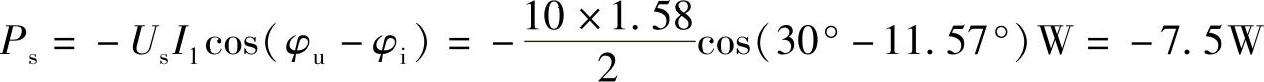

电容元件和电感元件的平均功率为0W。

39.求图6-53所示电路中电流源的平均功率。

解：方法一

电流源端口的等效阻抗为

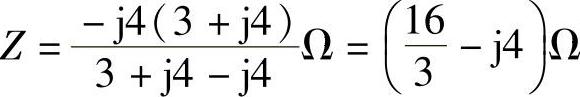
等效阻抗的平均功率为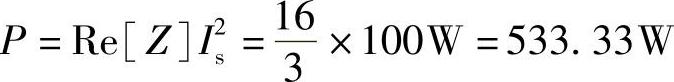

电流源的功率为 P_I=-P=-533.33W

方法二

设电阻支路的电流为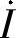，如图6-54所示。利用分流公式可求得

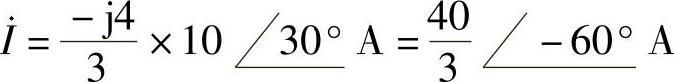
电阻消耗的功率等于电流源提供的功率，因而有

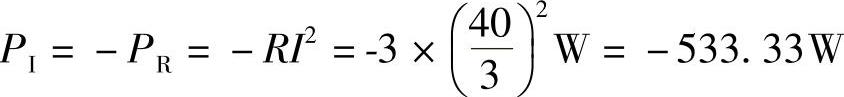
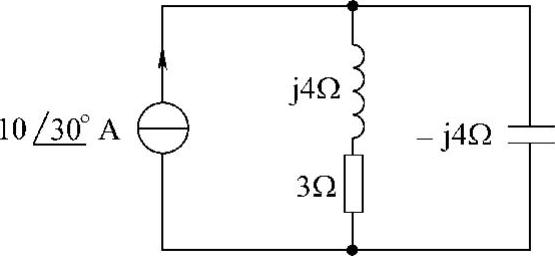
图6-53 题39图

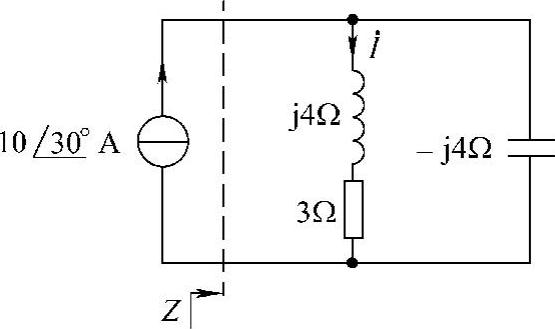
图6-54 题39解图

40.电路如图6-55所示，求：

（1）Z_L取何值时能从前端电路获得最大功率？

（2）最大功率是多少？

解：化简图6-55电路，如图6-56所示。其中

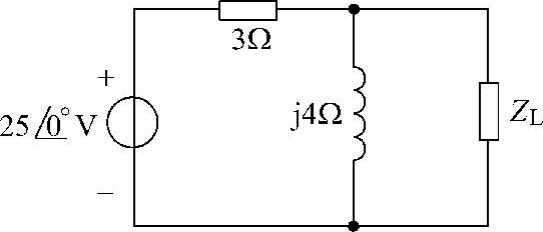
图6-55 题40图

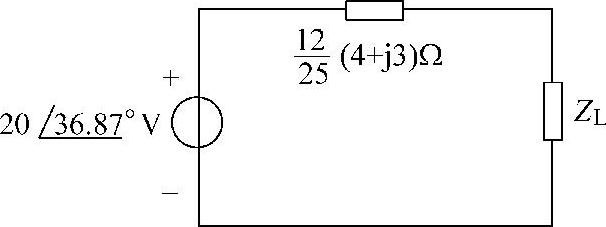
图6-56 题40解图

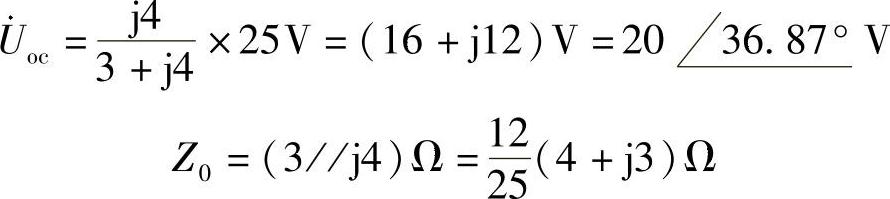
由图6-56可直接得知：

（1）当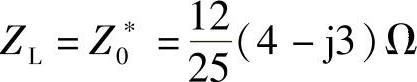时，能从前端电路获得最大功率。

（2）这时，最大功率为

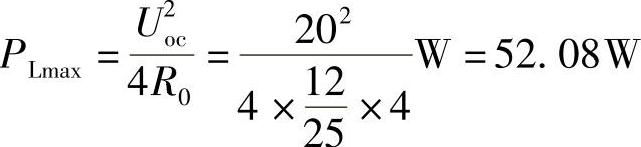
41.求图6-57所示电路中：

（1）Z_L取何值能获最大功率？

（2）最大功率是多少？

解：化简电路，如图6-58所示。其中

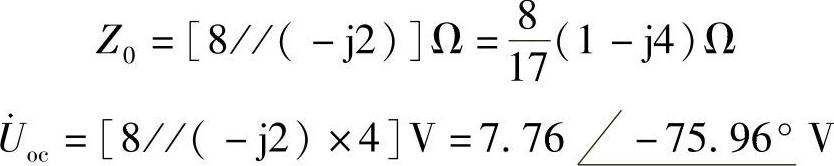
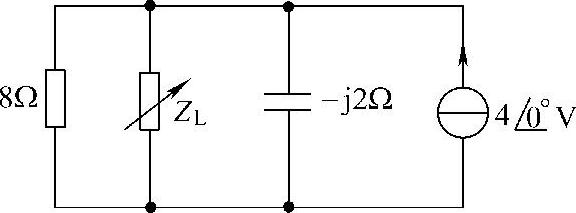
图6-57 题41图

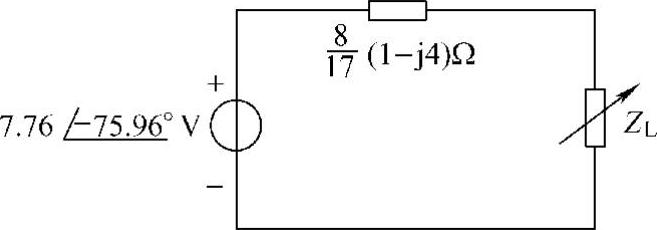
图6-58 题41解图

由图6-58可直接求得

（1）当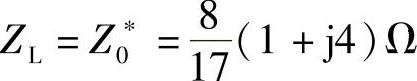时，能获得最大功率。

（2）此时的最大功率为

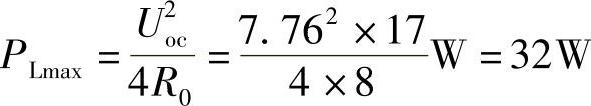
42.请标出图6-59所示耦合电感的同名端。

解：设1、3端口电流如图6-60所示。1端口流入电流产生的磁力线用实线表示。3端口流入电流产生的磁力线用虚线表示。因磁力线方向一致，故两个电流流入端为同名端，即1、3端子互为同名端，2、4端子也互为同名端，如图6-60所示。

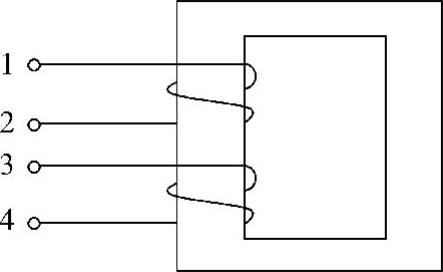
图6-59 题42图

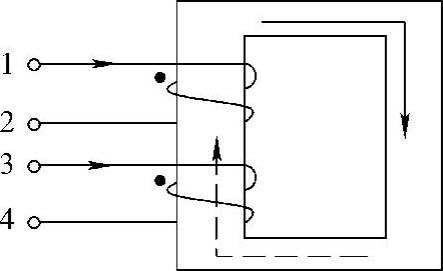
图6-60 题42解图

43.请写出图6-61所示两个耦合电感的电压电流关系。

解：图6-61a所示电路的电压电流关系为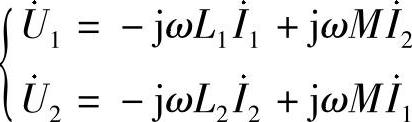

图6-61b所示电路的电压电流关系为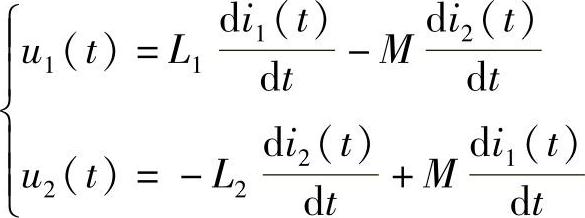

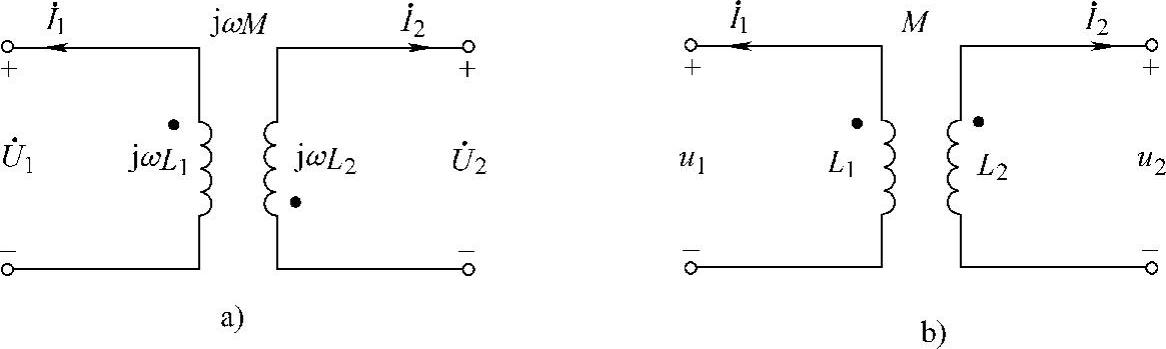
图6-61 题43图

44.求图6-62所示电路的ab端口等效电感。

解：设耦合电感的端口电压、电流，在所示参考方向下画受控源等效电路，如图6-63所示。端口电压电流关系为

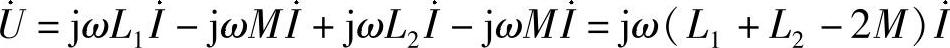
则ab端口等效电感为 L=L₁+L₂-2M

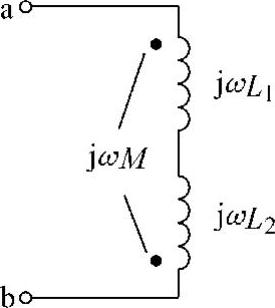
图6-62 题44图

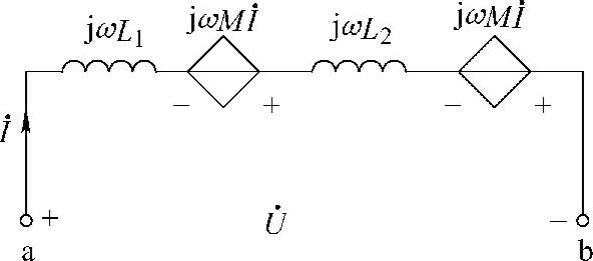
图6-63 题44解图

45.电路如图6-64所示，求i₁（t）和i₂（t）。

解：做去耦等效相量电路，如图6-65所示。

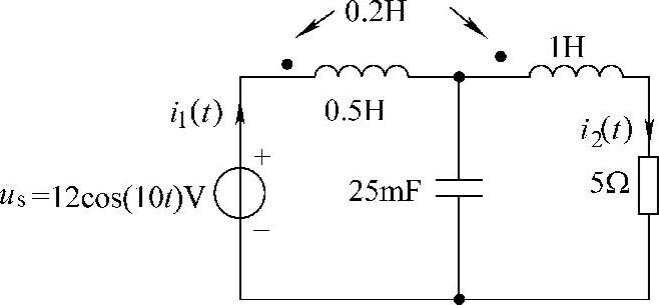
图6-64 题45图

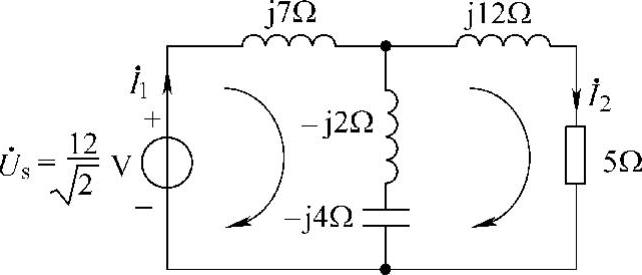
图6-65 题45解图

列网孔电流方程

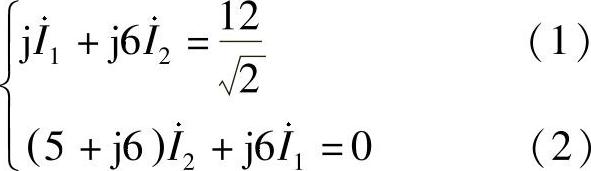
式（2）整理为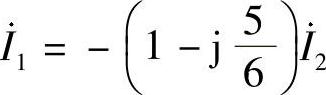，代入式（1），得

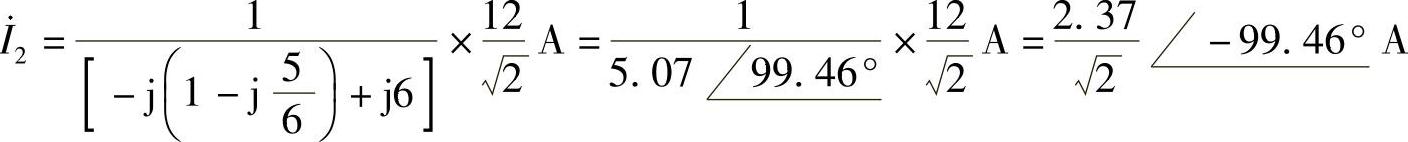
则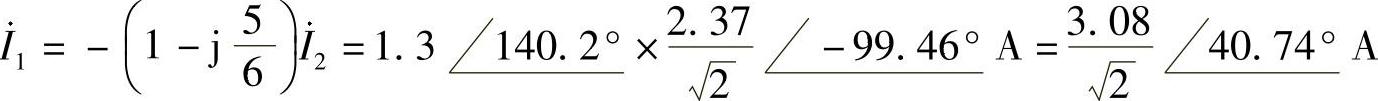做相量反变换，得

i₂（t）=2.37cos（10t-99.46°）A

i₁（t）=3.08cos（10t+40.74°）A

46.求图6-66所示电路的输入阻抗Z_i。

解：二次回路阻抗为Z₂₂=（20-j5+j40）Ω=（20+j35）Ω

二次回路在一次的反应阻抗为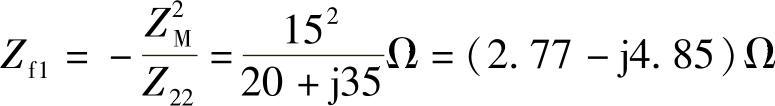

则有 Z_i=10+j12+Z_f1=（10+j12+2.77-j4.85）Ω=（12.77+j7.15）Ω

47.求图6-67所示电路中的电压。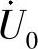

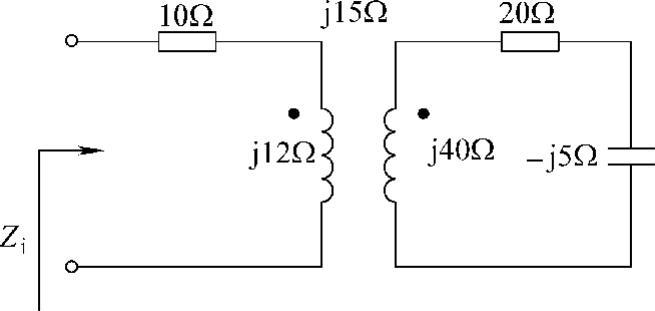
图6-66 题46图

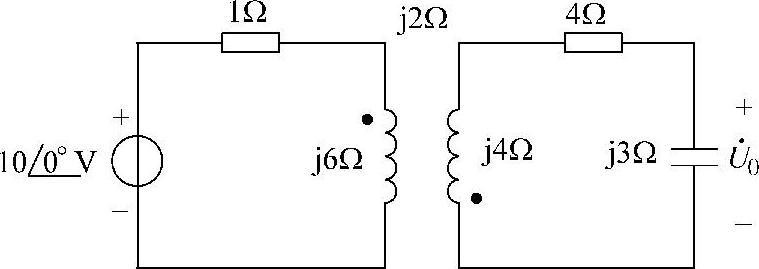
图6-67 题47图

解：做二次等效电路，如图6-68所示。其中

一次回路阻抗为 Z₁₁=（1+j6）Ω

一次回路在二次的反应阻抗为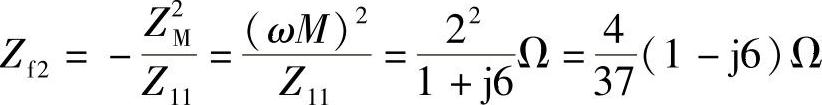

二次回路的等效电压源为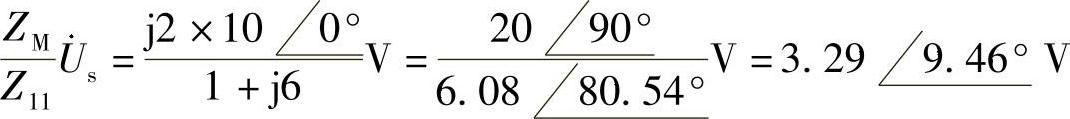

利用分压公式解得

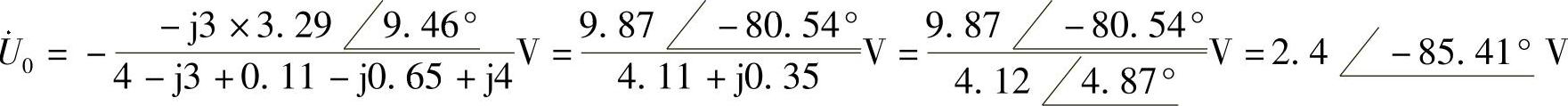
48.电路如图6-69所示，已知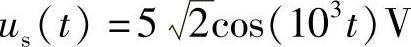，L1=L₂=2H，R₁=500Ω，M=1H，C₁=C₂=0.5μF，求：

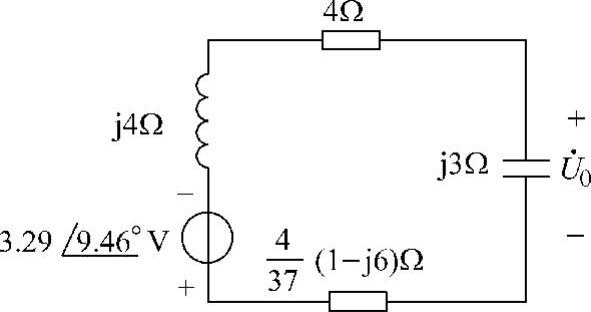
图6-68 题47解图

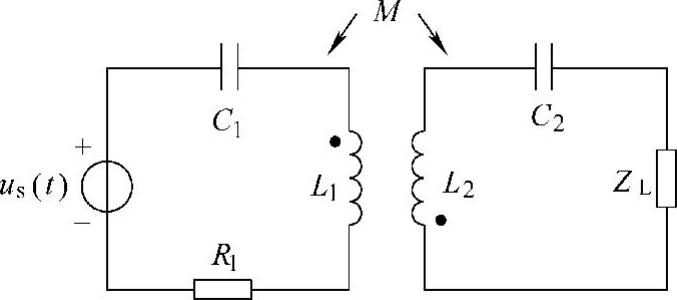
图6-69 题48图

（1）负载Z_L为何值时可获最大功率？

（2）最大功率是多少？

解：本题求解的是二次回路的问题，所以要用二次等效电路分析。其中

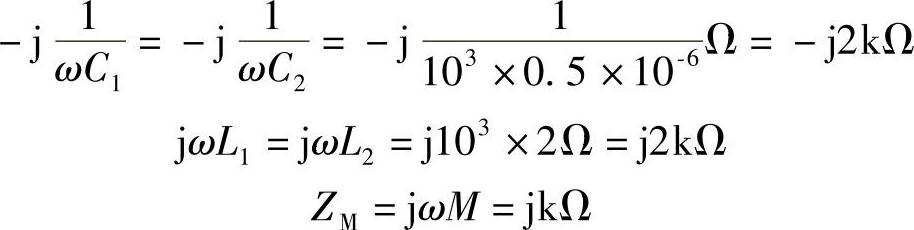
一次回路的阻抗为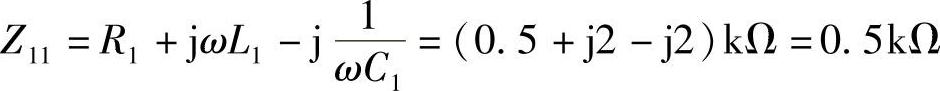

一次回路在二次的反应阻抗为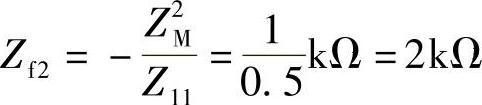

二次回路的等效电压源为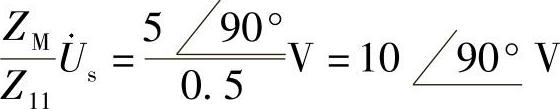

二次等效电路如图6-70所示。

由图可知：

(1)当Z₁=Z₀^*=（2+j2-j2）kn=2k.Q.时，能获最大功率。

（2）最大功率为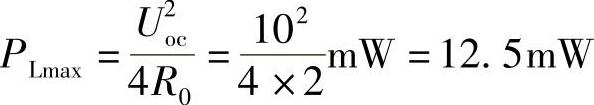

49.请写出图6-71所示理想变压器的电压电流关系式。

解：图6-71a的电压电流关系如下：

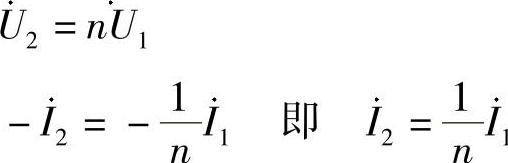
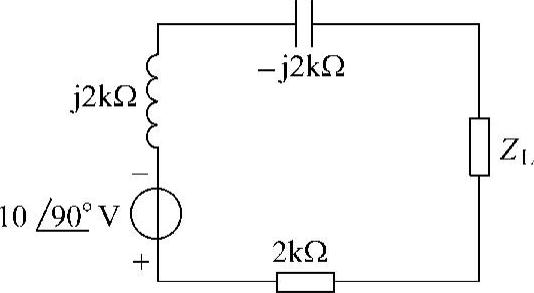
图6-70 题48解图

图6-71b的电压电流关系如下：

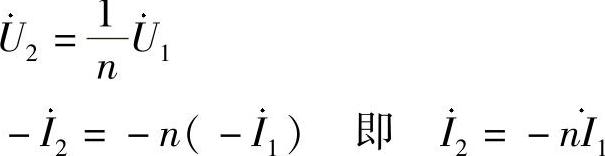
图6-71 题49图

50.求图6-72所示电路中的电流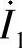和。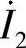

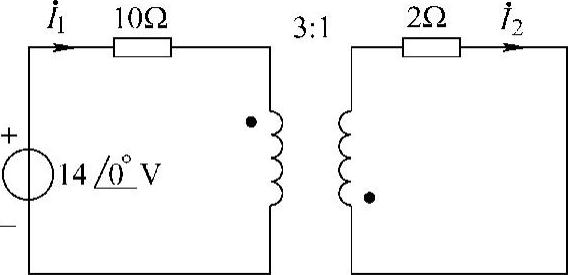
图6-72 题50图

解：利用理想变压器的阻抗变换关系，做一次等效电路，如图6-73所示，其中折合阻抗为n²Z_L=3³×2Ω。由图可求一次回路的电流为

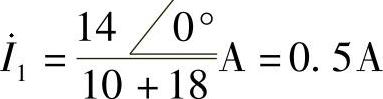
再根据理想变压器的电流关系，得

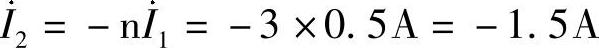
51.电路如图6-74所示，为使10Ω电阻获得最大功率。求：

（1）匝比n。

（2）计算10Ω电阻获取的最大功率。

解：方法一：用一次等效电路分析。

做理想变压器的一次等效电路，如图6-75所示。根据最大功率传输定理知

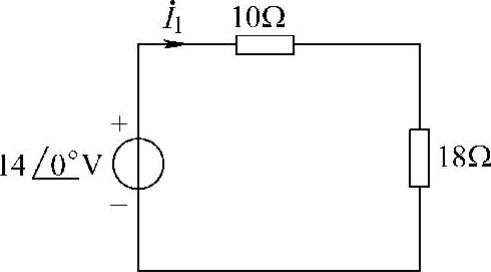
图6-73 题50解图一次等效电路

（1）当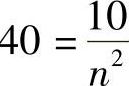，即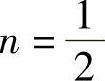时，负载10Ω电阻能获最大功率。

（2）此时获得的最大功率为

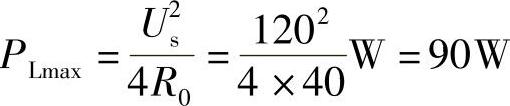
方法二：用二次等效电路分析。

二次等效电路如图6-76所示。根据最大功率传输定理知

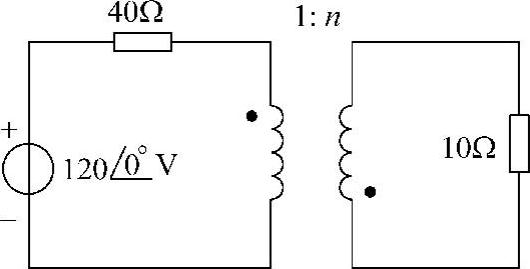
图6-74 题51图

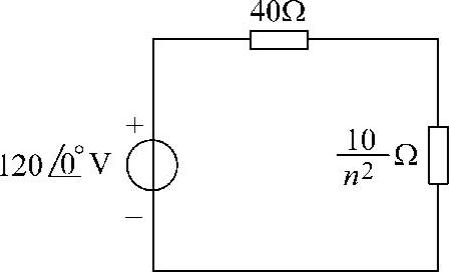
图6-75 题51解图一次等效电路

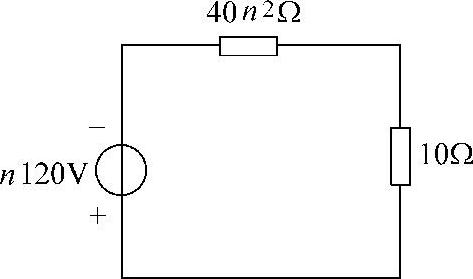
图6-76 题51解图二次等效电路

（1）当40n²=10，即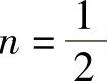时，10Ω负载获最大功率。

（2）最大功率为

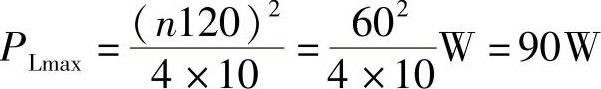
52.电路如图6-77所示。求输出电压。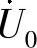

解：做理想变压器的一次等效电路，如图6-78所示。其中

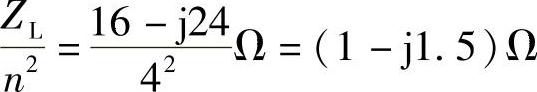
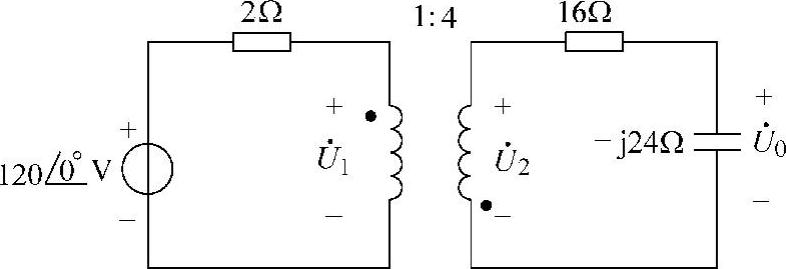
图6-77 题52图

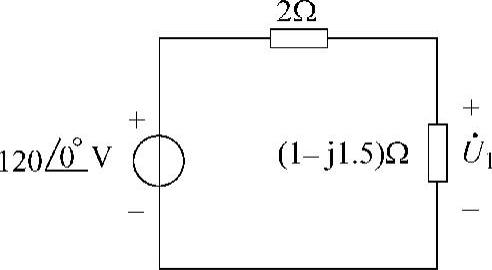
图6-78 题52解图一次等效电路

在图6-78所示电路中，利用分压关系，得

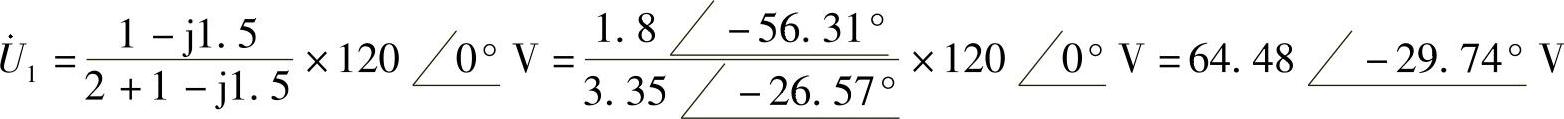
由理想变压器的电压电流关系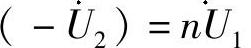可知

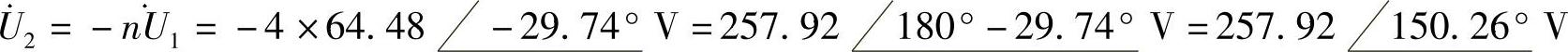
回到图6-77所示电路中，由分压关系可得

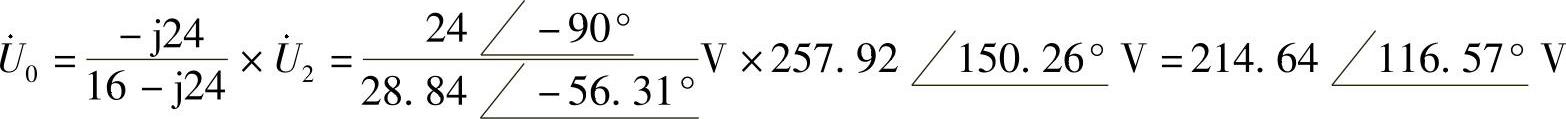
53.电路如图6-79所示，请用结点法求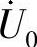和。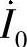

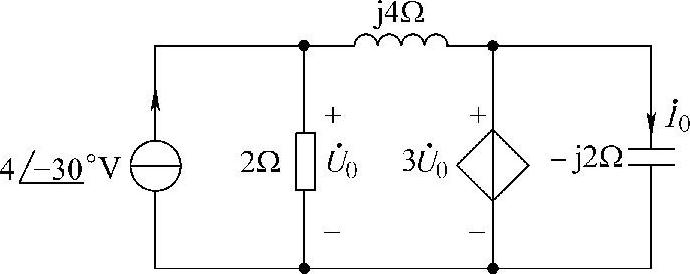
图6-79 题53图

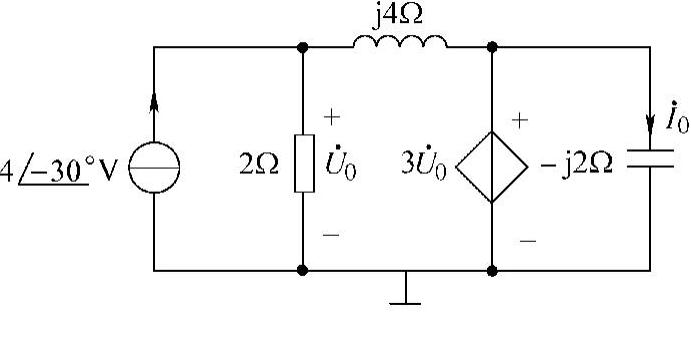
图6-80 题53解图

解：设参考结点，如图6-80所示。两个结点电压分别为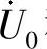和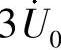。列结点电压方程

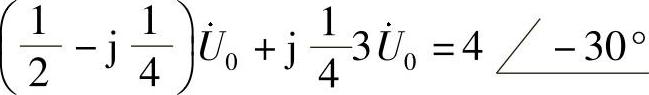
解得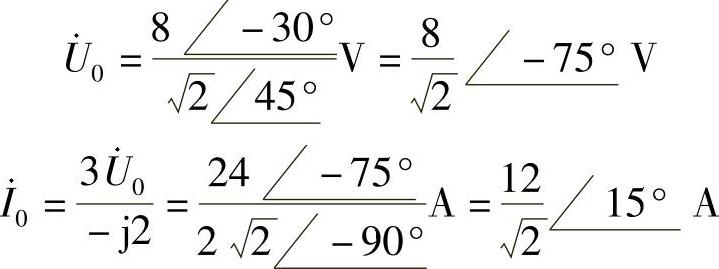

54.若某城镇的高压配电电压为AC10kV，送入用户端口变压器的一次，如图6-81所示，变压器的输出电压为AC220V。

（1）求变压器的匝比n。

（2）接在220V电压上的100W白炽灯要从高压线上获取多大的电流？

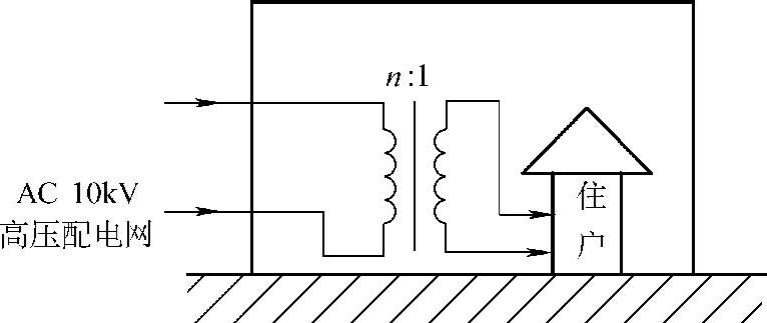
图6-81 题54图

解：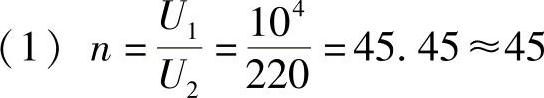

（2）方法一：二次回路的电流为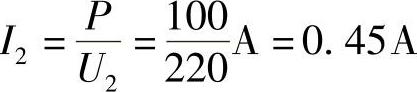

则一次回路，即高压线上的电流为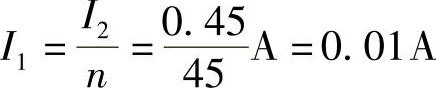

方法二：根据理想变压器输入功率与输出功率相等的特点，已知P_出=100W，P_入=U₁I₁，则

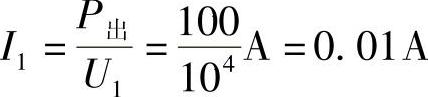
55.在图6-82a所示电路中，电容起阻隔前端放大器电路的直流、把放大的语音信号传递给扬声器的作用。图中放大器电路和电容可视为电源，扬声器作为负载，等效电路如图6-82b所示，求：

（1）在什么频率上扬声器能获最大功率？

（2）若U_s=4.6V，扬声器在该频率点上获取的最大功率是多少？

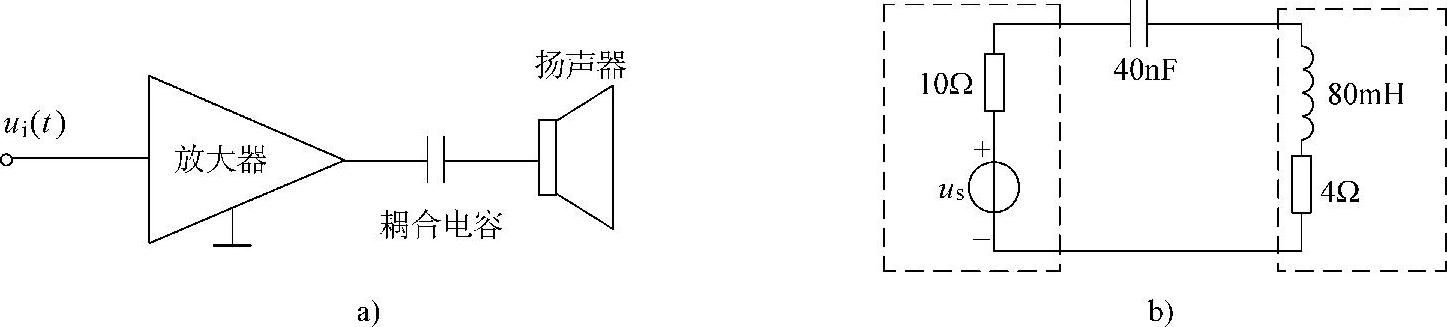
图6-82 题55图

解：（1）图6-82b回路电流为

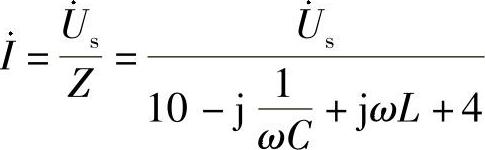
当电流值I最大时，即回路阻抗Z最小时，扬声器能获最大功率。这时有

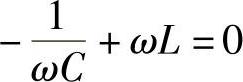
即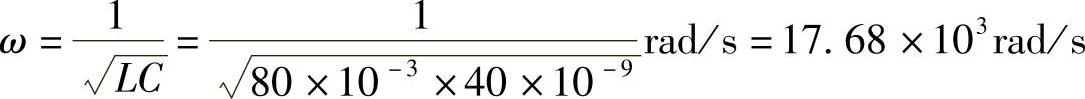

或者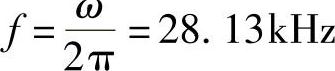

（2）在（1）问的频率上，回路电流为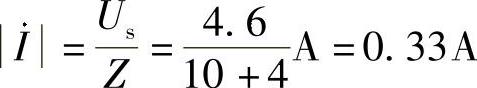

扬声器获得的功率为 P=R_LI²=4×0.33²W=0.44W