相量法分析正弦稳态电路的步骤

（1）相量法的分析步骤

用相量法分析正弦稳态电路，通常采用如下步骤：

1）进行相量变换。把正弦电压与电流变换成相量，把时域电路变换为相量电路。在电路变换时，支路互联关系不变，电量的参考方向不变，元件的时域电路模型用相量电路模型替换。如果给出的是相量电路，可省略这步。

2）求相量解。根据相量电路模型、相量形式的两类约束条件、各种分析方法和电路定理，在相量域里列、解复数代数方程，求出响应的相量解。

3）进行相量反变换。若需要正弦函数形式的解，则要对相量解作相量反变换。

（2）阻抗串、并联计算公式

阻抗串联等效公式

阻抗并联等效公式

在图6-3所示参考方向下，分压公式为

在图6-4所示参考方向下，分流公式为

图6-3 两个阻抗串联

图6-4 两个阻抗并联

（3）常用分析方法

常用分析法除了等效变换法、网孔法、结点法、回路法之外，还有以下几种：

1）分析含耦合电感电路的两种方法：①去耦等效法。耦合电感的去耦等效电路如图6-5所示。把一个T形连接的耦合电感等效变换为由三个独立电感构成的T形连接电路，然后用分析独立电感电路的方法进行分析。②受控源等效分析法。该方法适用于任意连接形式的耦合电感电路，因此比去耦等效法应用更广泛，是一种基本方法。在受控源等效电路模型中，把互感电压分量用电流控制电压源等效，然后再按已学过的受控源电路的分析方法去分析电路。

图6-5 T形连接的去耦等效变换

a）同名端连接的去耦等效电路 b）异名端连接的去耦等效电路(www.xing528.com)

2）分析空心变压器电路的一次、二次等效电路法。在分析空心变压器电路时，用一次、二次等效电路可以简化分析。通常，求一次回路的电量时，用一次等效电路，如图6-6b所示；求二次回路的电量或最大功率传输问题时，则用二次等效电路，如图6-6c所示。图中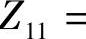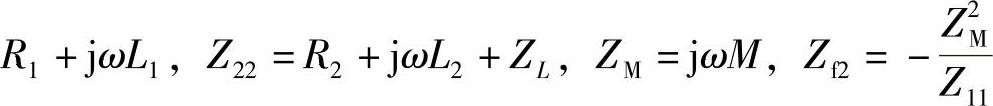，和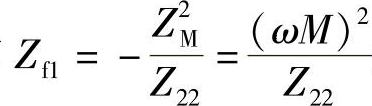为反映阻抗。

图6-6 空心变压器电路的一次、二次等效电路变换法

a）空心变压器电路模型 b）空心变压器的一次等效电路 c）空心变压器的二次等效电路

图6-7 理想变压器的阻抗变换

3）分析含理想变压器电路的阻抗变换法。图6-7a所示的理想变压器一次、二次绕组之间没有电联系。分析这类结构的理想变压器电路时，可利用阻抗的等效变换，把接在二次绕组上的负载阻抗等效变换到一次绕组两端，得到如图6-7b所示的一次等效电路。调节匝比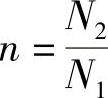可改变阻抗大小，但不改变阻抗的性质。换句话说，通过理想变压器进行阻抗变换，只改变阻抗的模Z_L，不改变阻抗角θ_L。

（4）常用电路定理

①叠加定理

②戴维南定理

③诺顿定理

④最大功率传输定理

在正弦稳态电路中，有阻抗共轭匹配和阻抗模匹配两种功率传输情况。

·当负载阻抗的实部R_L和虚部X_L可以分别调节时，有如下共轭匹配定理：

当负载Z_L=Z₀∗时，即取R_L=R₀，当X_L=-X₀时，负载Z_L能从前端电路获得最大功率，最大平均功率为

·当负载阻抗的模Z_L可以调节、角度θ_L不能变动时，有如下模匹配定理：

当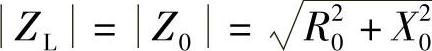时，负载Z_L能从前端电路获得最大功率。