【摘要】：正弦电量的数学表达式为 f=Fmcos正弦电量的三要素：振幅Fm、角频率和初相φ这三个参数一旦确定，正弦函数f就能唯一确定，所以称这三个参数为正弦电量的三要素。相位差θ两个正弦电量的相位之差定义为相位差。在分析正弦稳态电路时，通常遇到的是两个同频率正弦电量的相位差。同频率正弦电量相位差有以下几种可能的情况：1）θ12=φ1-φ2>0，称f1超前f2一个θ12角度。
正弦电量的数学表达式为 f（t）=Fmcos（ωt+φ）
（1）正弦电量的三要素：
振幅Fm、角频率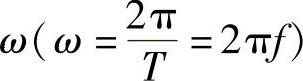
和初相φ这三个参数一旦确定，正弦函数f（t）就能唯一确定，所以称这三个参数为正弦电量的三要素。
（2）相位差θ
两个正弦电量的相位之差定义为相位差。在分析正弦稳态电路时，通常遇到的是两个同频率正弦电量的相位差。设两个同频率正弦电量分别为
f1（t）=F1mcos（ωt+φ1）
f2（t）=F2mcos（ωt+φ2）
则它们的相位差为
θ12=（ωt+φ1）-（ωt+φ2）=φ1-φ2 （6-1）
也就是说，两个同频率正弦电量的相位差等于它们的初相之差，为常数。
相位差的取值范围为-π≤θ≤π。(www.xing528.com)
同频率正弦电量相位差有以下几种可能的情况：
1）θ12=φ1-φ2>0，称f1（t）超前f2（t）一个θ12角度。或者说f2（t）滞后f1（t）一个θ12角度。
2）θ12<0，称f2（t）超前f1（t）一个θ12角度。或者说f1（t）滞后f2（t）一个θ12角度。
3）θ12=0，称f1（t）与f2（t）同相。
4）θ12=±π，称f1（t）与f2（t）反相。
5）θ12=±π/2，称f1（t）与f2（t）正交。
（3）有效值F
周期函数的有效值定义为
特殊地，当周期函数是正弦函数时，有效值为
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
