电路题优化：图4-3、图4-5、图4-8、图4-9的电路题精解

1.电路如图4-3所示，计算：

（1）电流I。

（2）把电压源改为10V，电流I是多少？

解：设各支路电流及参考方向如图4-3所示，令I′=1A，则有

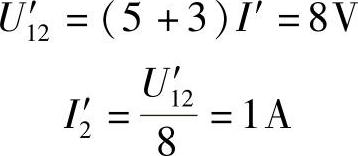
I₁′=I₂′+I′=（1+1）A=2A

U_s′=1×I₁′+U₁′₂=（1×2+8）V=10V

所以响应与激励的比例系数为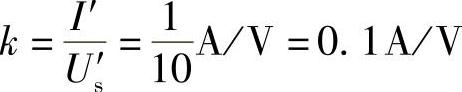

（1）当U_s=1V时，I=kU_s=0.1×1A=0.1A。

（2）当U_s=10V时，I=kU_s=0.1×10A=1A。

2.电路如图4-4所示。

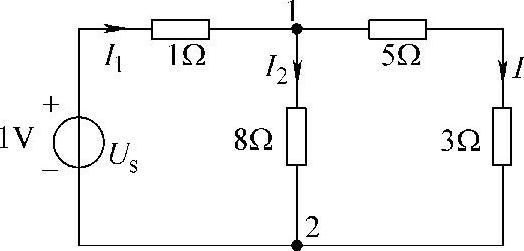
图4-3 题1图

（1）求电压U。

（2）若电流源减至1μA，电压U是多少？

解：设各支路电流及参考方向如图4-4所示。

令U′=2V，则有

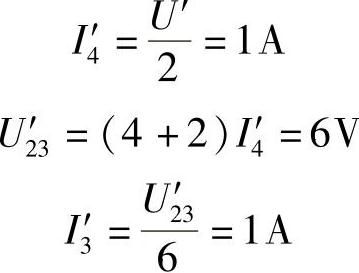
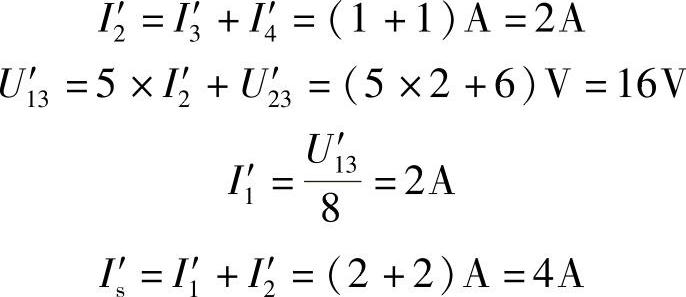
所以响应与激励的比例系数为

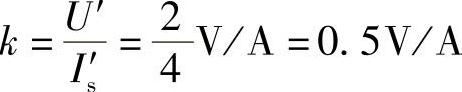
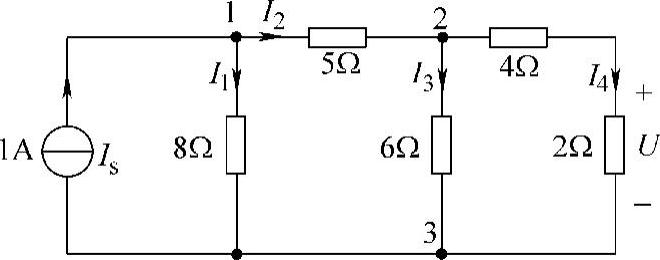
图4-4 题2图

（1）当I_s=1A时，U=kI_s=0.5×1V=0.5V

（2）当I_s=1μA时，U=kI_s=0.5×1μV=0.5μV

3.试用叠加定理求图4-5所示各电路中的电压U。

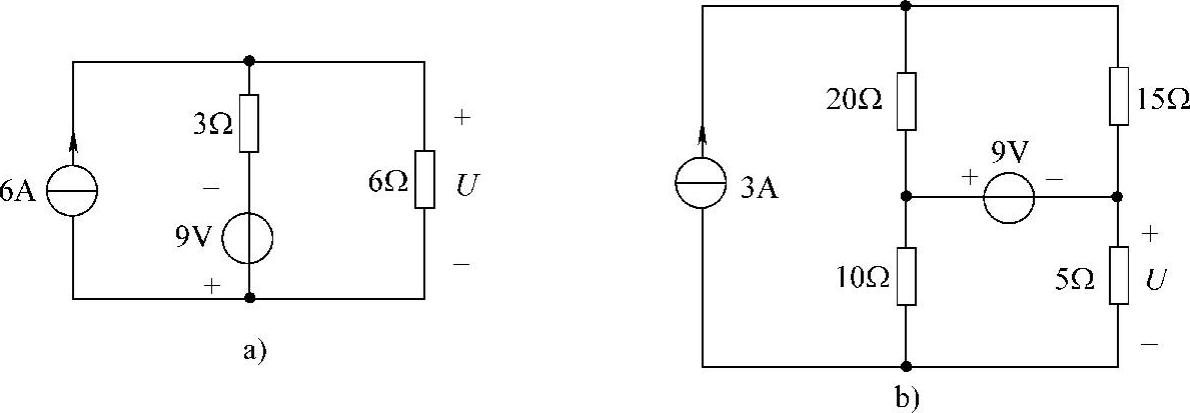
图4-5 题3图

解：（1）运用叠加定理分析

1）求9V电压源单独作用时产生的电压U′。

当电压源单独作用时，独立电流源置零，即断开6A电流源，如图4-6所示，可得

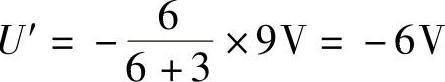
2）求6A电流源单独作用时产生的电压U″。

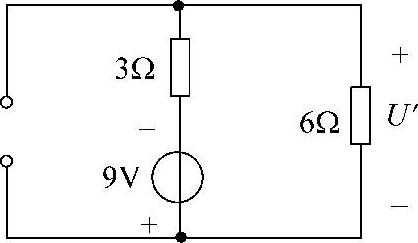
图4-6 题3解图

当电流源单独作用时，独立电压源置零，即9V电压源短路，如图4-7所示，可得

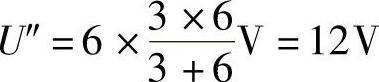
3）叠加求电压U，可得

U=U′+U″=（-6+12）V=6V

（2）运用叠加定理分析

1）求9V电压源单独作用时产生的电压U′。

当电压源单独作用时，独立电流源置零，即断开3A电流源，如图4-8所示，可得

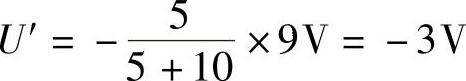
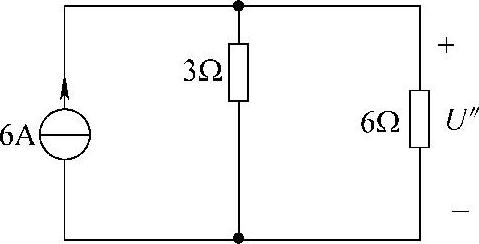
图4-7 题3解图

2）求6A电流源单独作用时产生的电压U″。

当电流源单独作用时，独立电压源置零，即9V电压源短路，如图4-9所示。这时，电路元件之间是串、并联关系，可得

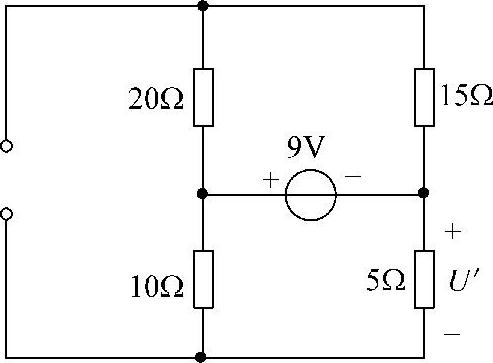
图4-8 题3解图

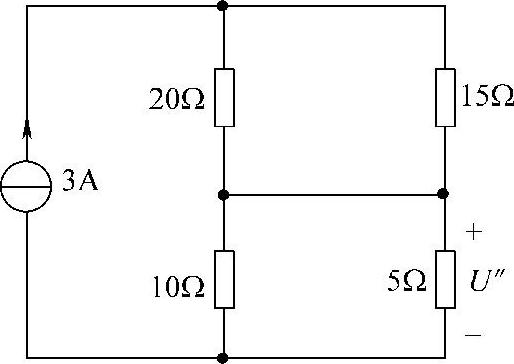
图4-9 题3解图

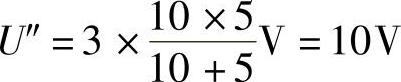
3）叠加求电压U，可得

U=U′+U″=（-3+10）V=7V

4.试用叠加定理求图4-10所示电路中的电流I。

解：运用叠加定理分析。

（1）求2V电压源单独作用时产生的电流I′

当电压源单独作用时，独立电流源置零，即断开1A电流源，如图4-11所示。这时，12Ω和4Ω电阻的并联支路未接任何电源，可得

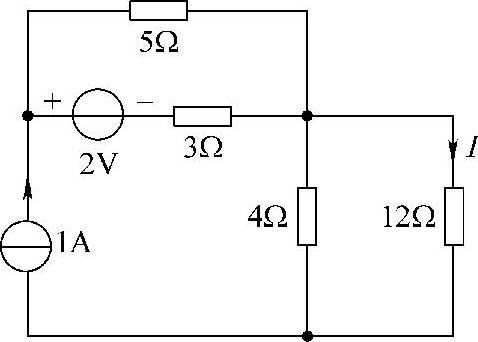
图4-10 题4图

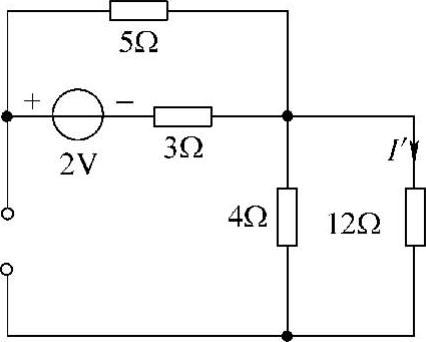
图4-11 题4解图

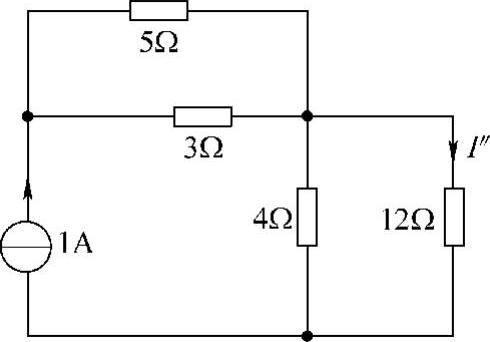
图4-12 题4解图

I′=0

（2）求1A电流源单独作用时产生的电流I″

当电流源单独作用时，独立电压源置零，即2V电压源短路，如图4-12所示。利用分流公式可求得

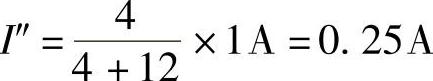
（3）叠加求电流I

I=I′+I″=（0+0.25）A=0.25A

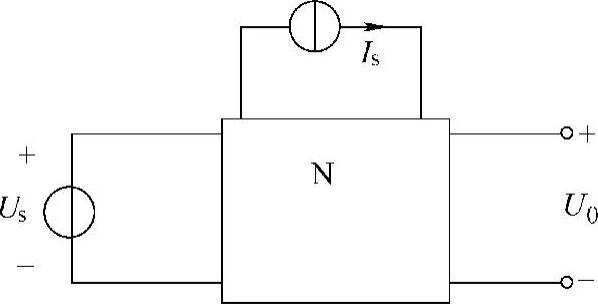
图4-13 题5图

5.电路如图4-13所示，N是线性无源电路，已知：当U_s=1V，I_s=2A时，U₀=0V，当U_s=2V，I_s=5A时，U₀=-2V。求：当U_s=2V，I_s=2A时的U₀。

解：由题意知，这是有两个独立源的线性电阻网络，故两个激励I_s和U_s与响应U之间存在着以下的线性关系：

U=k₁U_s+k₂I_s

把已知的两组数据代入上式，有

0=k₁+2k₂

-2=2k₁+5k₂

联立以上两个方程，解得

k₁=4

k₂=-2

则激励与响应的线性方程为

U=4U_s-2I_s

当U_s=2V，I_s=2A时，有

U=（4×2-2×2）V=4V

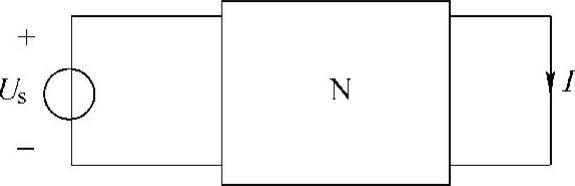
图4-14 题6图

6.在图4-14所示电路中，电路N是含源线性电阻电路，已知：当U_s=0V时，I=4mA，当U_s=10V时，I=-2mA。求：当U_s=-15V时的I。

解：由题意知，这是有两组独立源的线性电阻网络，一组独立源是激励U_s，另一组是含源线性电阻电路N中的独立源。设含源线性电阻电路N中的独立源产生的响应为I′，则这两组激励与响应I之间存在着以下的线性关系：

I=kU_s+I′

把已知的两组数据代入上式，有

4=0+I′

-2=10k+I′

联立以上两个方程，解得

k=-0.6mA/V

I′=4mA

则激励与响应的线性方程为

I=-0.6U_s+4

当U_s=-15V时，有

I=[-0.6×（-15）+4]mA=13mA

7.电路如图4-15所示，已知：当3A电流源单独作用时，向网络提供54W功率，且U₂=12V，当2A电流源单独作用时，向网络提供28W功率，且U₃=8V。求：两个电流源同时作用时，各电流源的功率。

解：根据题意，当3A电流源单独作用时，有

U₂′=12V和3U₃′=54W

即 U₃′=18V

图4-15 题7图

当2A电流源单独作用时，有

U″₃=8V和2U₂″=28W

即 U₂″=14V

所以两个电流源同时作用时，有

U₂=U₂′+U″₂=（12+14）V=26V

U₃=U₃′+U″₃=（18+8）V=26V

2A电流源的功率为

P₂=-2U₂=-2×26W=-52W 即释放52W功率

3A电流源的功率为

P₃=-3U₃=-3×26W=-78W 即释放78W功率

8.电路如图4-16b所示，请把图4-16a表格中的缺省电流数据填写出来。

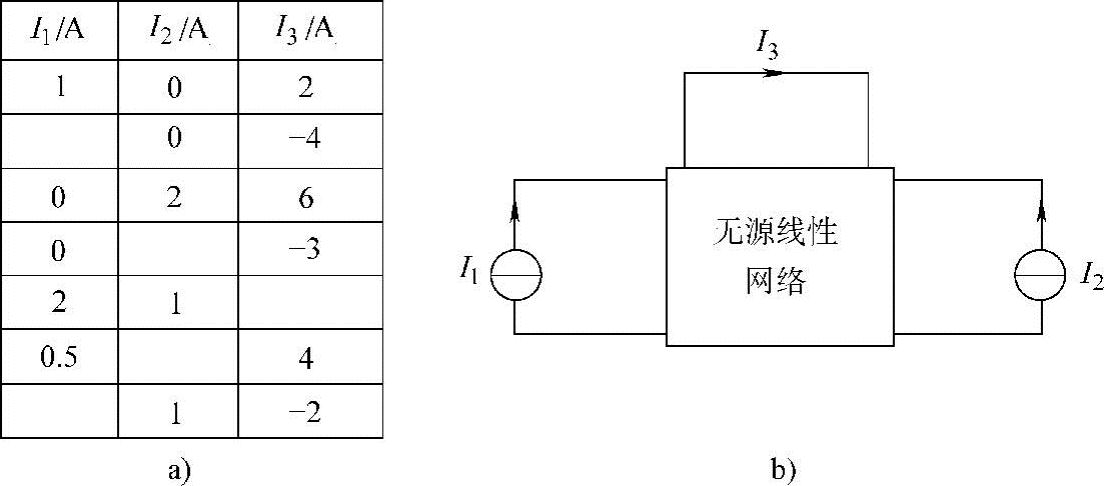
图4-16 题8图

解：由题意知，这是有两个独立源的线性电阻网络，故两个激励I₁和I₂与响应I₃之间存在着以下的线性关系：

I₃=k₁I₁+k₂I₂

把已知的两组数据代入上式，有

2=k₁

6=2k₂

联立以上两个方程，解得

k₁=2

k₂=3

则激励与响应的线性方程为

I₃=2I₁+3I₂

当I₂=0，I₃=-4A时，有I₃=2I₁+3I₂=2I₁=-4，可得I₁=-2A

当I₁=0，I₃=-3A时，有I₃=2I₁+3I₂=3I₂=-3，可得I₂=-1A

当I₁=2A，I₂=1A时，有I₃=2I₁+3I₂=（2×2+3×1）A=7A

当I₁=0.5A，I₃=4A时，有I₂=（I₃-2I₁）/3=（4-2×0.5）/3A=1A

当I₂=1A，I₃=-2A时，有I₃=2I₁+3I₂=2I₁+3×1=-2，可得I₁=-2.5A

9.试用叠加定理求图4-17所示电路中的电压U。

解：（1）求4V电压源单独作用时产生的电压U′

当电压源单独作用时，独立电流源置零，即断开2A电流源，如图4-18所示。可得3U′+U′=4即U′=1V

（2）求2A电流源单独作用时产生的电压U″

当电流源单独作用时，独立电压源置零，即4V电压源短路，如图4-19。可得

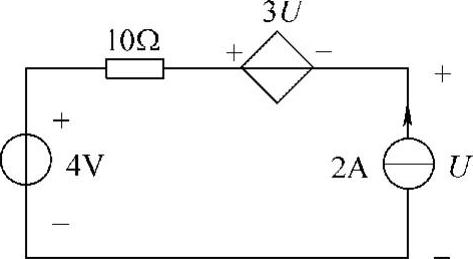
图4-17 题9图

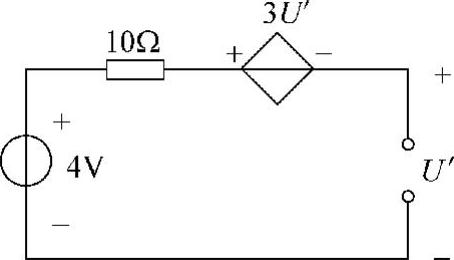
图4-18 题9解图

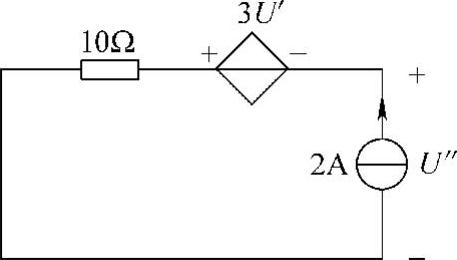
图4-19 题9解图

3U″+U″-2×10=0 即 U″=5V

（3）叠加求电压U

U=U′+U″=（1+5）V=6V

10.电路如图4-20所示，求ab端口的戴维南等效电路。

解：（1）求ab端口的开路电压U_oc

设网孔电流、端口开路电压参考方向如图4-20所示，有

10I₁+40I₁=4

得I₁=0.08A。而I₂=3A，则

U_oc=20I₂+40I₁=（20×3+40×0.08）V=63.2V

（2）求端口的等效电阻R₀

把原图中的电压源短路，电流源断开，得到如图4-21所示的纯电阻电路。利用电阻串并联化简公式，得端口等效电阻为

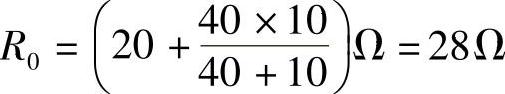
可得该电路ab端口的戴维南等效电路如图4-22所示。

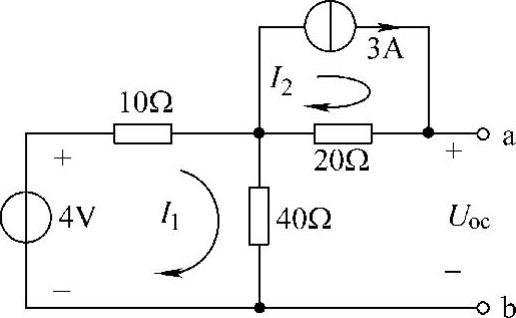
图4-20 题10图

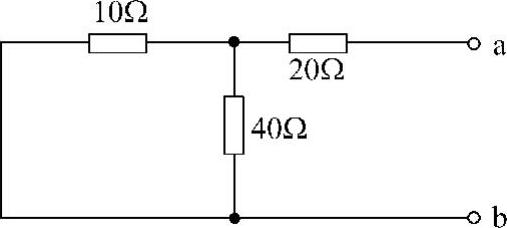
图4-21 题10解图

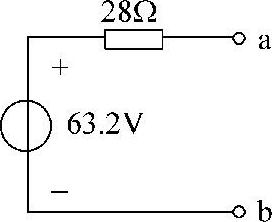
图4-22 题10解图

11.试求图4-23所示各电路的戴维南等效电路。

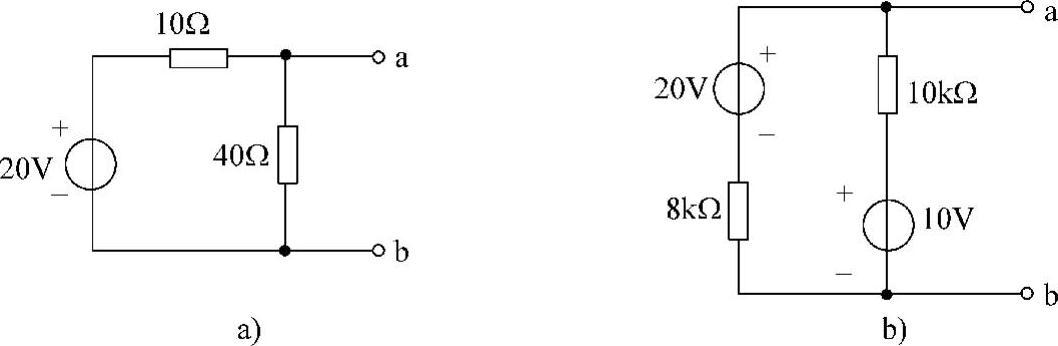
图4-23 题11图

解：（1）图4-23a的戴维南等效电路如图4-24所示。

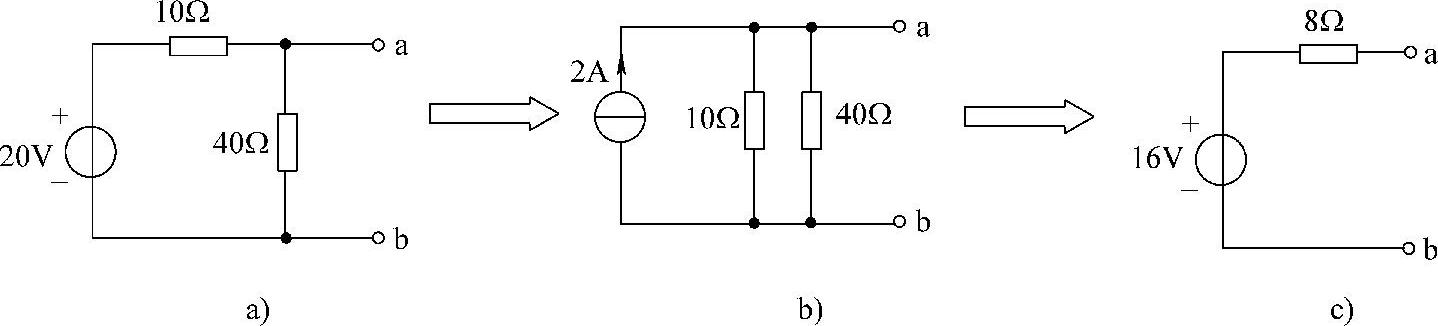
图4-24 题11解图

（2）

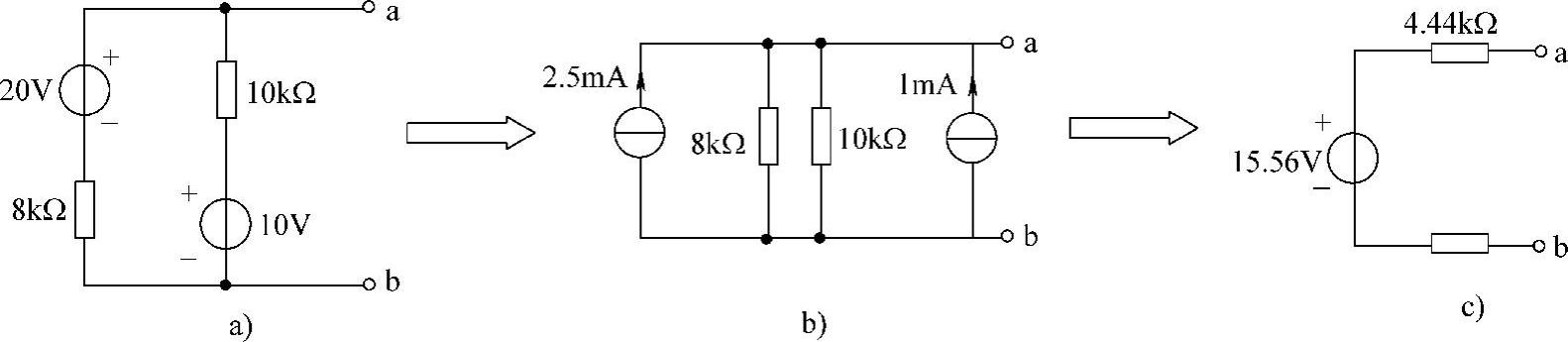
图4-25 题11解图

12.电路如图4-26所示，求ab端口的戴维南等效电路。

解：第一步：求ab端口的开路电压U_oc。设支路电流、端口开路电压参考方向如图4-26所示，有

60I+30=30（2-I） 得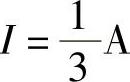

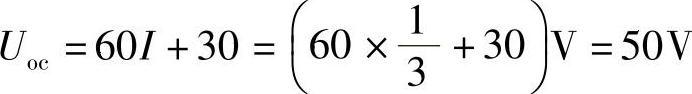
第二步：求端口的等效电阻R₀，把原图中的电压源短路，电流源断开，得到如图4-27所示的纯电阻电路。利用电阻串并联化简公式，得端口等效电阻为

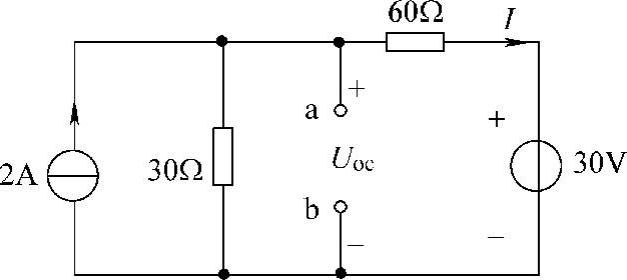
图4-26 题12图

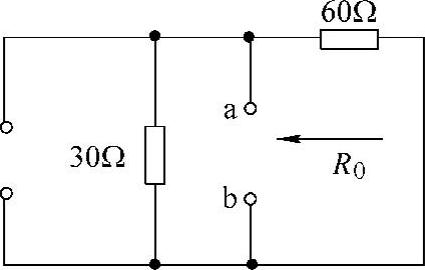
图4-27 题12解图

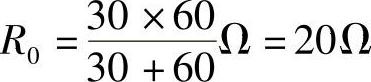
可得该电路ab端口的戴维南等效电路如图4-28所示。

13.试用戴维南定理求图4-29所示电路中的电流I。

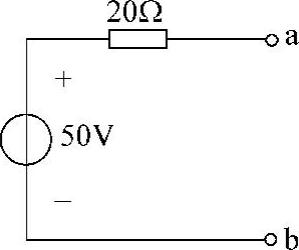
图4-28 题12解图(www.xing528.com)

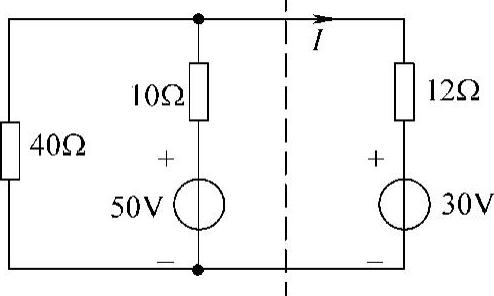
图4-29 题13图

解：先求虚线左边单口电路的戴维南等效电路。

第一步：求端口的开路电压U_oc，设端口开路电压参考方向如图4-30所示，有

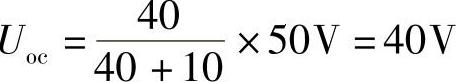
第二步：求端口的等效电阻R₀，把原图中的电压源短路，电流源断开，得到如图4-31所示的纯电阻电路。利用电阻串并联化简公式，得端口等效电阻为

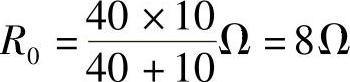
第三步：画原电路的等效电路，如图4-32所示。

第四步：求电流I。

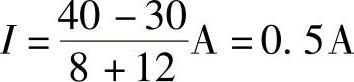
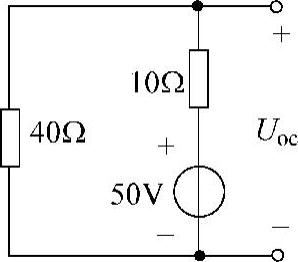
图4-30 题13解图

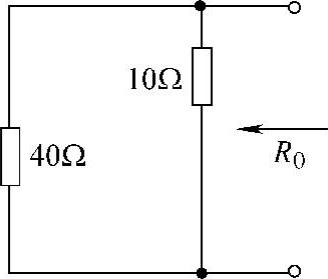
图4-31 题13解图

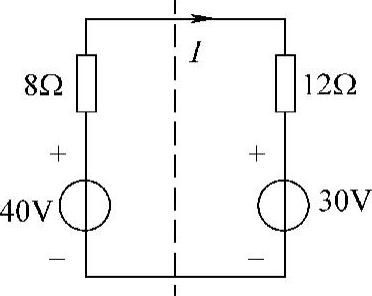
图4-32 题13解图

14.求图4-33所示电路的戴维南等效电路。

解：第一步：求ab端口的开路电压U_oc，设端口开路电压参考方向如图4-33所示，有

I=2A

则 U_oc=4I-10I=（4×2-10×2）V=-12V

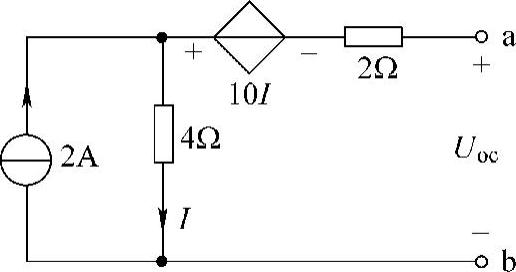
图4-33 题14图

第二步：求端口的等效电阻R₀，把原图中的电流源断开，受控电压源保留在电路中，得到如图4-34所示电路。设图4-34端口电流I₁与端口电压U参考方向关联，可得

I₁=I

U=2I₁-10I+4I=-4I1

则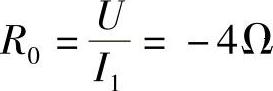

可得该电路ab端口的戴维南等效电路如图4-35所示。

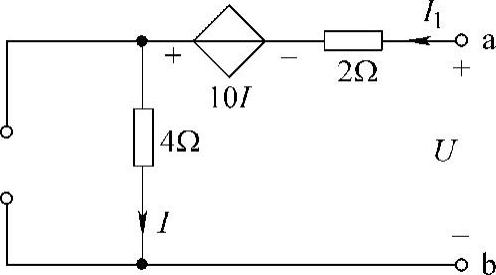
图4-34 题14解图

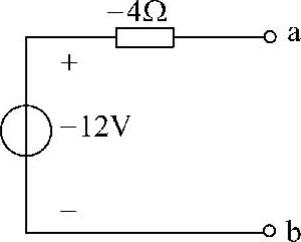
图4-35 题14解图

15.电路如图4-36所示，试用诺顿定理求电压U₀。

解：先求虚线左边单口电路的诺顿等效电路。

第一步：求端口的短路电流I_sc，设端口短路电流参考方向如图4-37所示，有

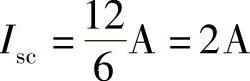
第二步：求端口的等效电阻R₀，把原图中的电压源短路，得到如图4-38所示的纯电阻电路。利用电阻串并联化简公式，得端口等效电阻为

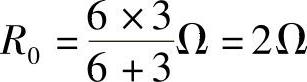
第三步：画原电路的等效电路，如图4-39所示。

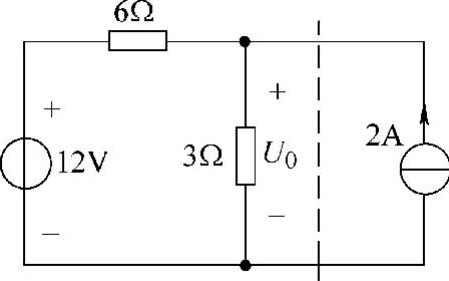
图4-36 题15图

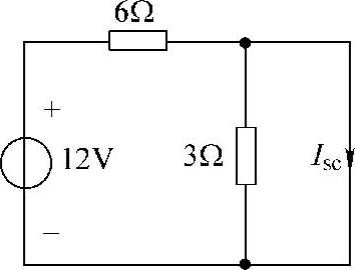
图4-37 题15解图

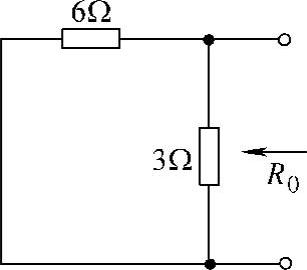
图4-38 题15解图

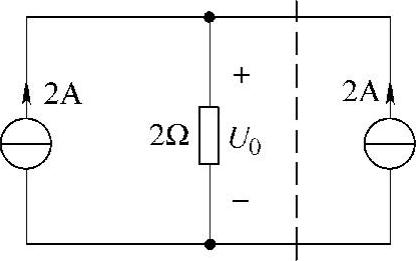
图4-39 题15解图

第四步：求电压U₀。

U₀=（2+2）×2V=8V

16.试用诺顿定理求图4-40所示电路中的电流I。

解：先求图4-40电路虚线左边单口电路的诺顿等效电路。

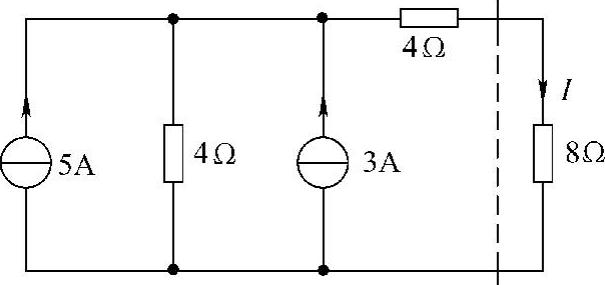
图4-40 题16图

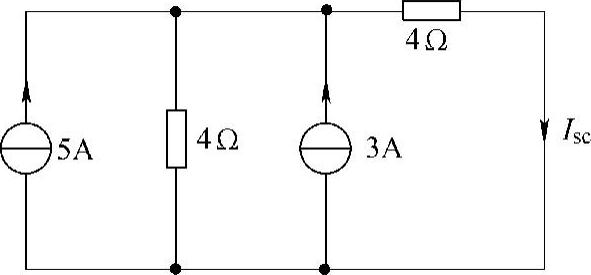
图4-41 题16解图

第一步：求端口的短路电流I_sc，设端口短路电流参考方向如图4-41所示。根据分流公式有

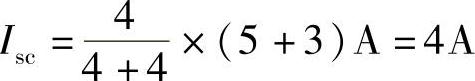
第二步：求端口的等效电阻R₀，把原图中的电流源开路，得到如图4-42所示的纯电阻电路。利用电阻串并联化简公式，得端口等效电阻为

R₀=（4+4）Ω=8Ω

第三步：画原电路的等效电路，如图4-43所示。

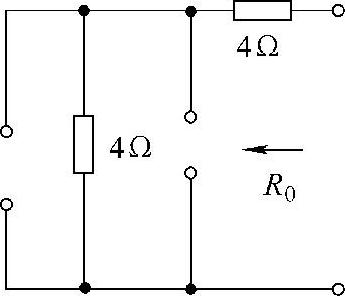
图4-42 题16解图

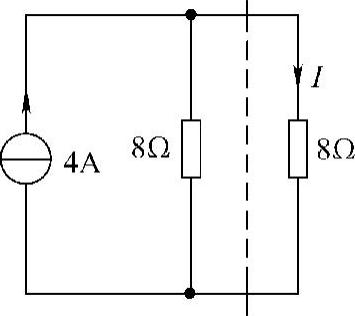
图4-43 题16解图

第四步：求电流I。

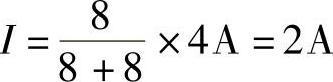
17.试用诺顿定理求图4-44所示电路中的电流I。

解：先将电路改画为图4-45所示电路，再求虚线左边单口电路的诺顿等效电路。

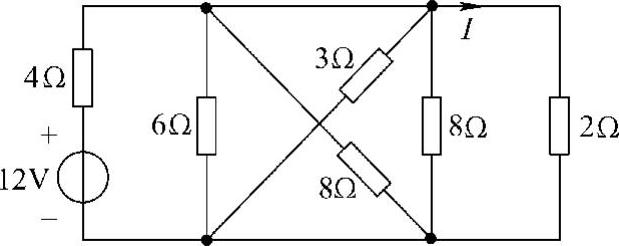
图4-44 题17图

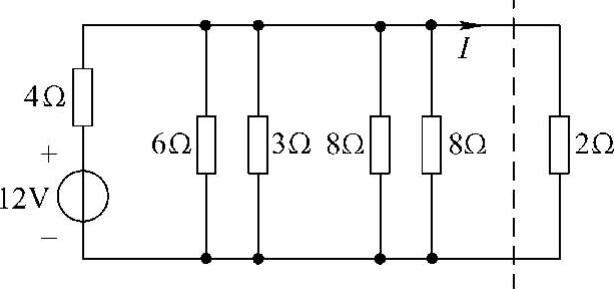
图4-45 题17解图

第一步：求端口的短路电流I_sc，设端口短路电流参考方向如图4-46所示，有

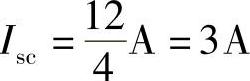
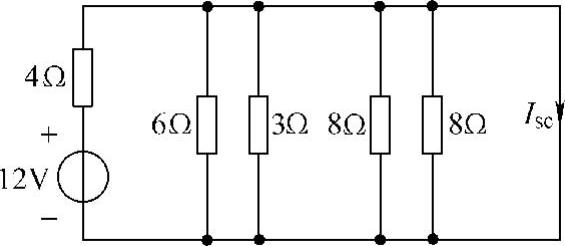
图4-46 题17解图

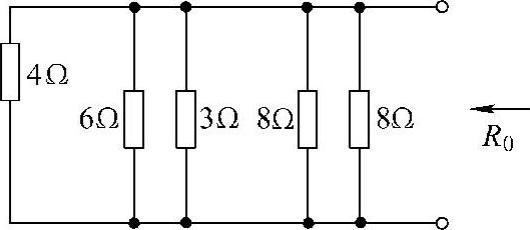
图4-47 题17解图

第二步：求端口的等效电阻R₀，把原图中的电流源开路，得到如图4-47所示的纯电阻电路。利用电阻串并联化简公式，得端口等效电阻为

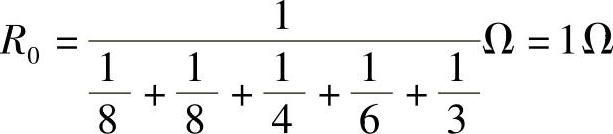
第三步：画原电路的等效电路，如图4-48所示。

第四步：求电流I。

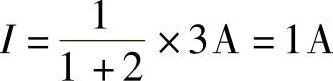
18.电路如图4-49所示，负载电阻R_L可变，求：

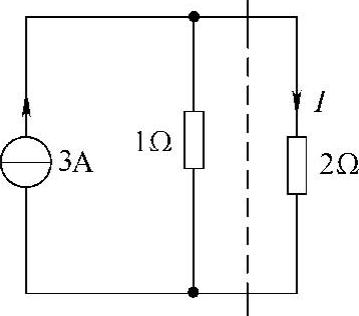
图4-48 题17解图

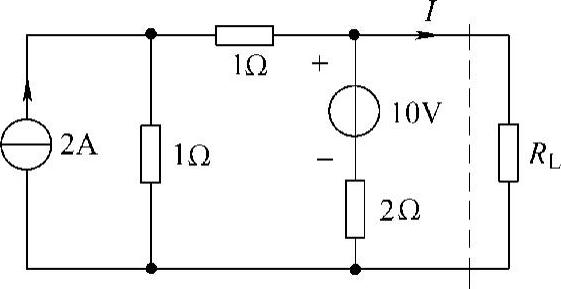
图4-49 题18图

（1）当R_L=1Ω时的电流I。

（2）当R_L=2Ω时的电流I。

解：先求虚线左边单口电路的戴维南等效电路。

第一步：求端口的开路电压U_oc，设网孔电流、端口开路电压参考方向如图4-50所示。

有网孔方程

（1+1+2）I-1×2=-10

得 I=-2A

而 U_oc=10+2I=[10+2×（-2）]V=6V

第二步：求端口的等效电阻R₀。把原图中的电压源短路，电流源断开，得到如图4-51所示的纯电阻电路。利用电阻串并联化简公式，得端口等效电阻为

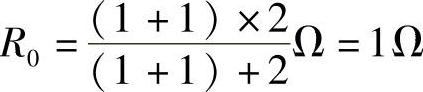
第三步：画原电路的等效电路，如图4-52所示，可得

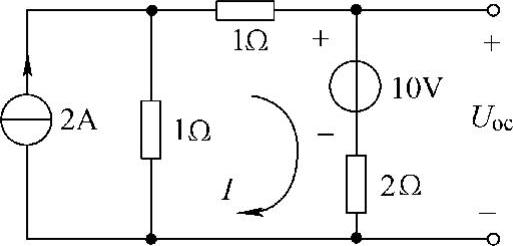
图4-50 题18解图

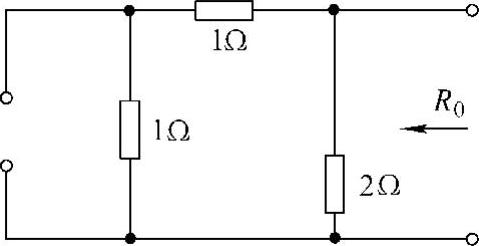
图4-51 题18解图

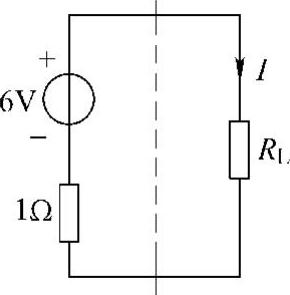
图4-52 题18解图

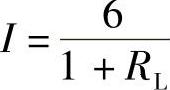
（1）当R_L=1Ω时，有

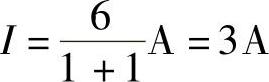
（2）当R_L=2Ω时，有

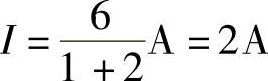
19.电路如图4-53所示，求：

（1）R_L为何值时能获最大功率？

（2）R_L的最大功率是多少？

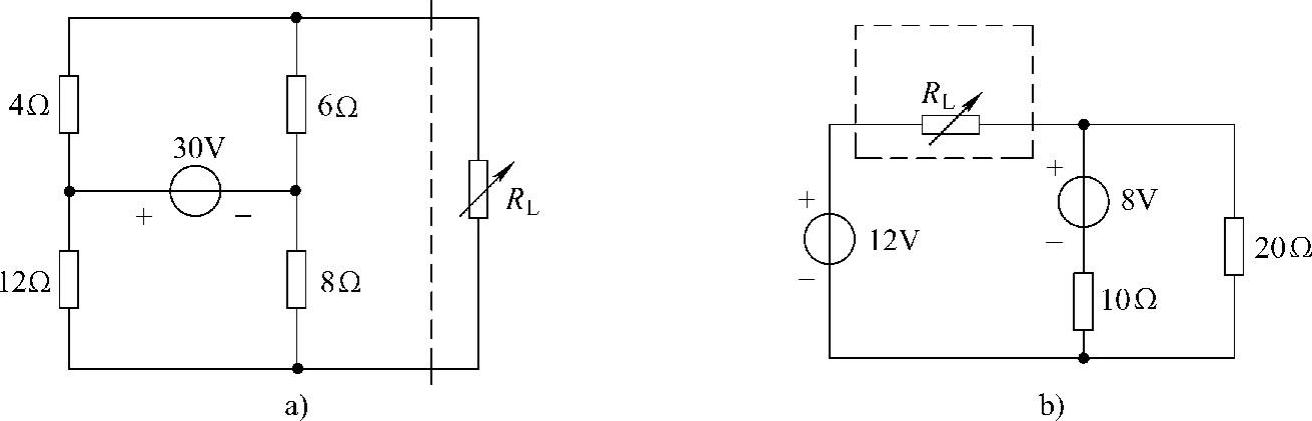
图4-53 题19图

解：（1）化简图4-53a虚线左边的电路。断开负载支路，得到如图4-54所示电路。利用分压公式，有

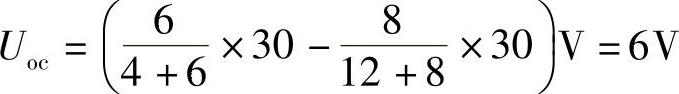
移去图4-53a中的负载支路，并将电压源置零，如图4-55所示，可得

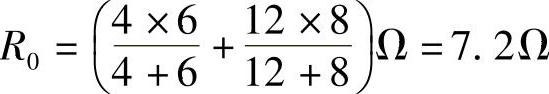
根据最大功率传输定理，当R₀=R_L=7.2Ω时，R_L能获最大功率，最大功率为

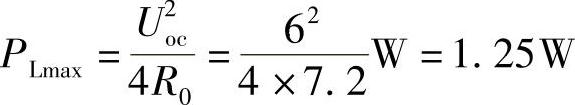
（2）化简图4-53b虚线外的电路。断开负载支路，得到如图4-56所示电路。利用分压公式，有

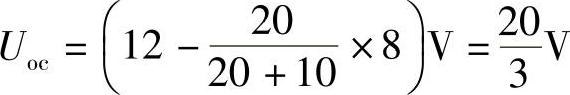
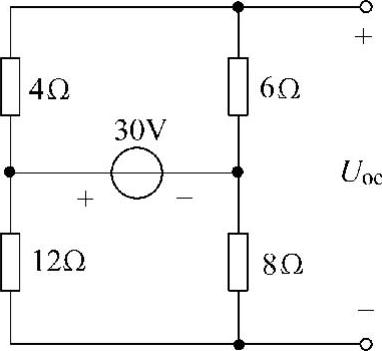
图4-54 题19解图

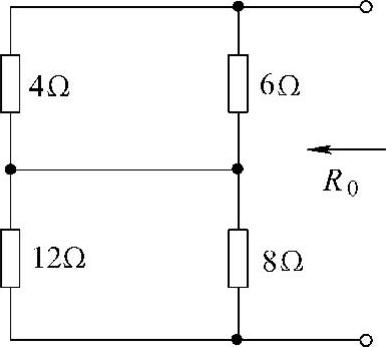
图4-55 题19解图

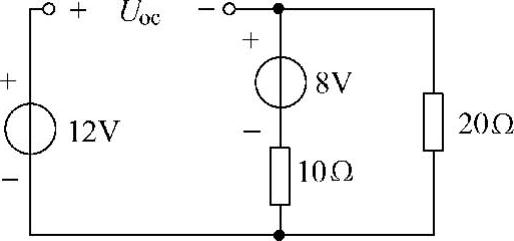
图4-56 题19解图

移去图4-53b中的负载支路，并将电压源置零，如图4-57所示，可得

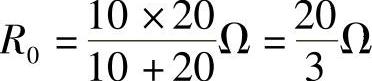
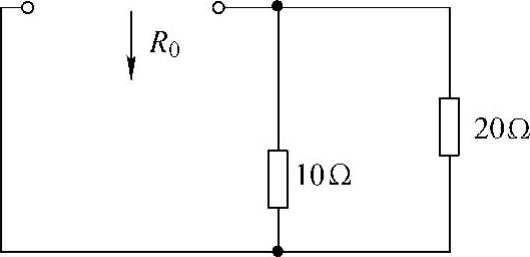
图4-57 题19解图

根据最大功率传输定理，当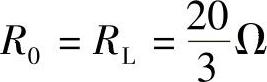时，R_L能获得最大功率，最大功率为

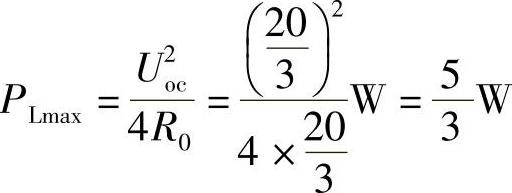
20.图4-58为晶体管电路模型，试求：

（1）R_L为何值时能获最大功率？

（2）最大功率是多少？

解：化简图4-58左边的电路。断开负载支路，得到如图4-59所示电路，有

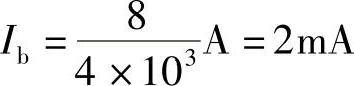
U_oc=-2I_b×40×10³=-2×2×10^-3×40×10³V=-160V

移去图4-58所示电路中的负载支路，并将电压源置零，如图4-60所示，此时I_b=0，可得R₀=40kΩ

根据最大功率传输定理，当R₀=R_L=40kΩ时，R_L能获最大功率，最大功率为

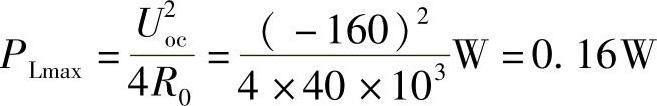
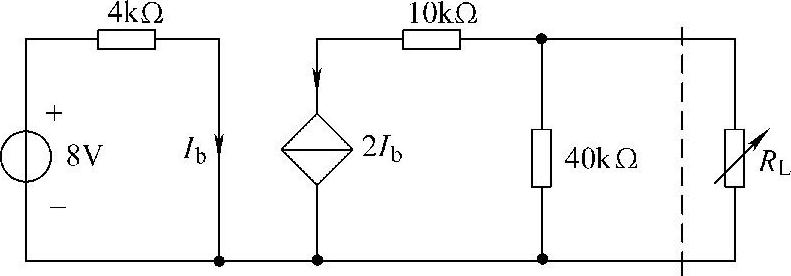
图4-58 题20图

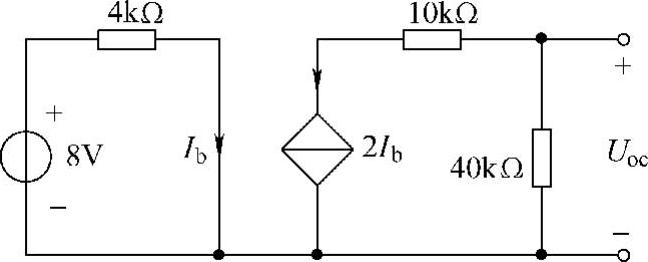
图4-59 题20解图

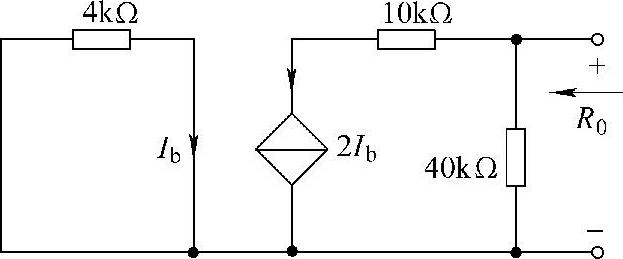
图4-60 题20解图

21.请分析图4-61所示电路有哪种端口等效电路？

解：根据电路等效的定义，先求该电路端口上的电压电流关系。设端口电压电流参考方向如图4-61所示，有

U=5I+10=5（I₁+2I-I）

可得I₁=2A。即端口电流为固定值，与端口上的电压无关，此电压电流关系与独立电流源的电压电流关系一样，故该电路的端口等效电路如图4-62所示。

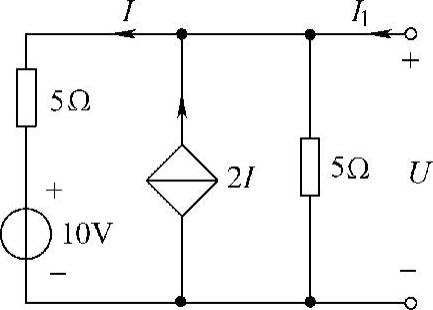
图4-61 题21图

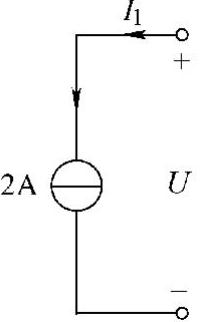
图4-62 题21解图

22.当汽车电池与汽车收音机连接时，提供12.5V电压，当该汽车电池与一组前灯连接时，提供11.7V电压。假定收音机等效为6.25Ω电阻，前灯等效为0.65Ω电阻。求汽车电池的戴维南和诺顿等效电路。

解：设汽车电池的戴维南等效电路如图4-63所示，则其接负载后的等效电路如图4-64所示。

当该汽车电池与汽车收音机连接，即R_L=6.25Ω时，有

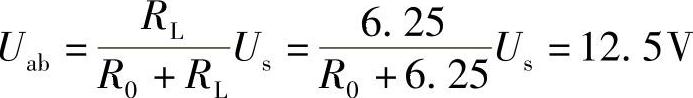
当该汽车电池与一组前灯连接，即R_L=0.65Ω时，有

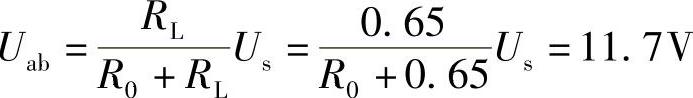
联立以上两式可解得

R₀=0.05Ω，U_s=12.6V

根据戴维南等效电路与诺顿等效电路的关系，可得该汽车电池的诺顿等效电路如图4-65所示。

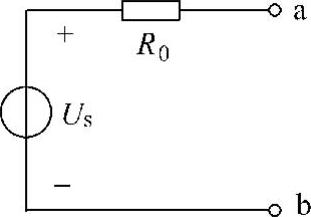
图4-63 题22解图

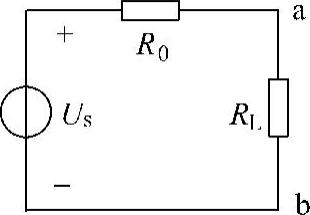
图4-64 题22解图

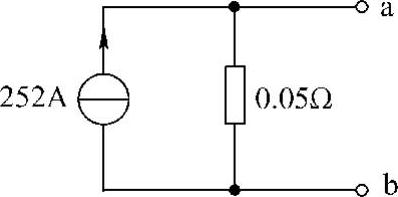
图4-65 题22解图

23.图4-66所示单口电路的戴维南等效电路可以通过测量来确定。假定单口电路a、b端被测量。当15kΩ电阻连接到a、b端时，电压U_ab的测量值为45V，当5kΩ电阻连接到a、b端时，电压U_ab的测量值为25V，求电路a、b端口的戴维南等效电路。

解：设该含源单口电路的戴维南等效电路如图4-67所示，则其接负载后的等效电路如图4-68所示。

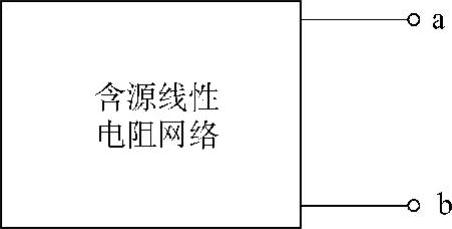
图4-66 题23图

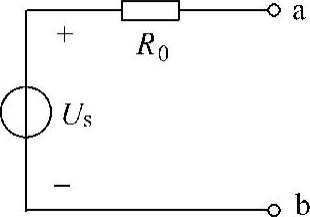
图4-67 题23解图

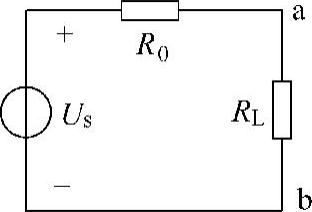
图4-68 题23解图

当R_L=15kΩ时，

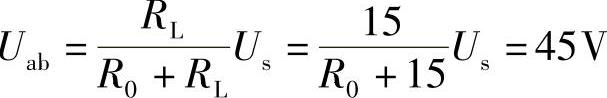
当R_L=5kΩ时，

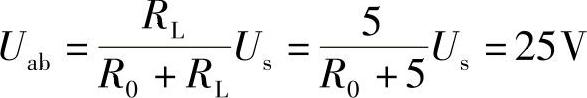
联立以上两式可解得

R₀=10kΩ，U_s=75V