本节利用Tensorflow环境,对基于深度神经网络的MIMO软判决检测方法进行验证,将从神经网络复杂度、检测性能、软判决性能三个方面对算法的性能进行仿真分析。
在神经网络中,隐藏层的个数以及每一层的节点数都将影响神经网络信号检测运算的计算复杂度,神经元节点数越小,复杂度就越低,但检测性能会降低。本算法采用三层隐藏层,对信号检测的误码率进行实验分析,数据集为2 000 000个(训练集=1 600 000,验证集=400 000),M=N=2,BPSK调制,神经网络第一层节点数设置为12,第二层设置为16,第三层设置为20,信噪比0≤SNR≤20 dB。为了对比所提算法的性能,同时对ML、MMSE、ZF算法进行仿真对比。如图8-4所示,横坐标代表信噪比,纵坐标代表误比特率,结果显示随着神经网络神经元节点数的增多,MIMO检测性能越来越好。当节点数多到一定程度时,达到了理论上的最优结果,性能趋于稳定。由算法的性能曲线可知,神经网络的检测性能与神经网络每层节点相关,且最优的深度神经网络MIMO信号检测相对于ML、MMSE、ZF算法,检测性能有了显著的提升。
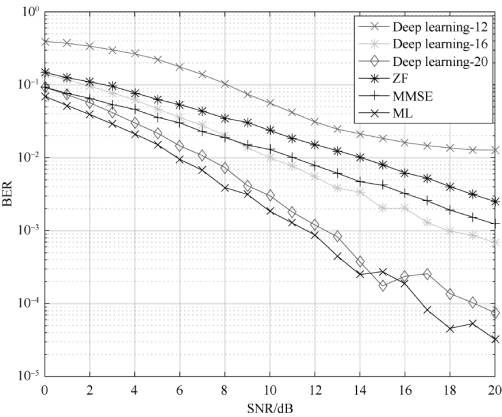
图8-4 不同复杂度的神经网络算法性能比较
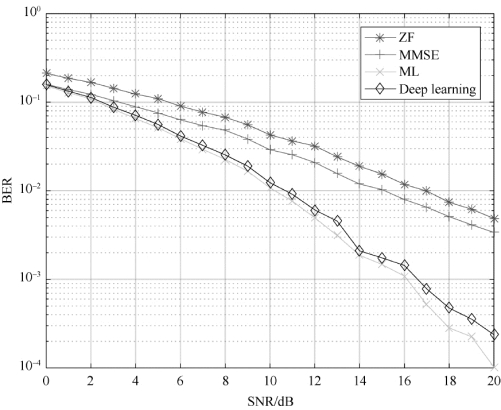
为进一步验证所提方法的检测性能,在BPSK调制方式下,数据集为2 000 000个(训练集=1 600 000,验证集=400 000),三层隐藏层神经元节点数均为20,M=N=2,对所提算法与ML、MMSE、ZF算法进行仿真对比,结果如图8-5所示。横坐标为信噪比,纵坐标为误比特率,通过比较可知,神经网络的检测性能在一定信噪比范围内,可以逼近最优的ML检测算法的性能,此外与ZF和MMSE两种经典的算法相比,具有更优越的性能。在QPSK调制方式下,数据集为4 000 000个(训练集=3 200 000,验证集=800 000),三层隐藏层神经元节点数为80,M=N=2,如图8-6所示,所提算法同样可以表现出良好的性能。
为了验证软判决方案的性能,首先对神经网络的硬判决进行实验分析。系统采用LDPC信道编码、QPSK调制方式,利用VIVO_5G研发的验证平台,分别在信道编码率coderate为0.1和0.8的环境下进行分析,如图8-7和图8-8所示,横坐标为信噪比,纵坐标为误块率。由实验结果可知,在高码率下,基于深度神经网络的硬判决输出经信道译码后的性能优于MMSE算法,但在低码率情况下,性能低于MMSE算法。
采用交叉熵最小准则进行神经网络软判决输出性能验证。系统采用LDPC信道编码和QPSK调制方式,分别在信道编码率coderate为0.1和0.8的环境下进行MIMO检测软判决输出性能实验,如图8-9和图8-10所示,横坐标为信噪比,纵坐标为误块率。实验结果显示,本节所提出的软判决技术经信道译码后,误码性能优于MMSE算法且逼近ML算法。在低码率时,虽不如MMSE算法的性能好,但与图8-8相比性能有所改善。
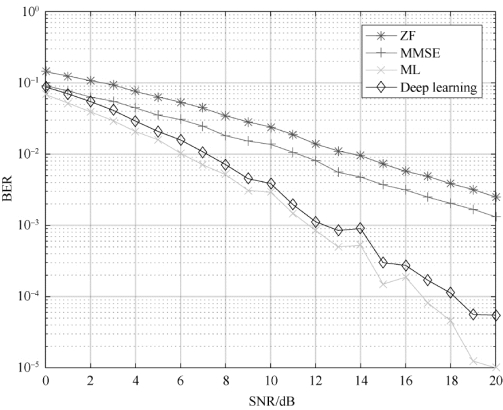
图8-5 基于BPSK的四种方法的信号检测
 (https://www.xing528.com)
(https://www.xing528.com)
图8-6 基于QPSK的四种方法的信号检测
上述结果表明,所提方法将深度学习用于MIMO检测,在检测性能良好的前提下,降低了计算复杂度。将信道状态信息和接收信号同时作为训练集,优化得到的神经网络具有适应时变信道的特性。将Sigmoid函数用于输出层激活函数,结合软判决技术,提高检测性能的同时,避免了求解LLR值的复杂问题。
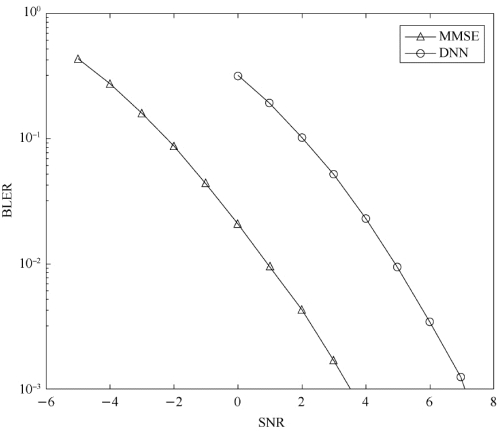
图8-7 coderate=0.1时的硬检测性能
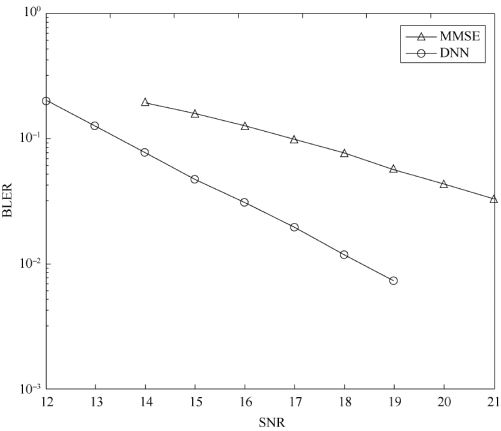
图8-8 coderate=0.8时的硬检测性能
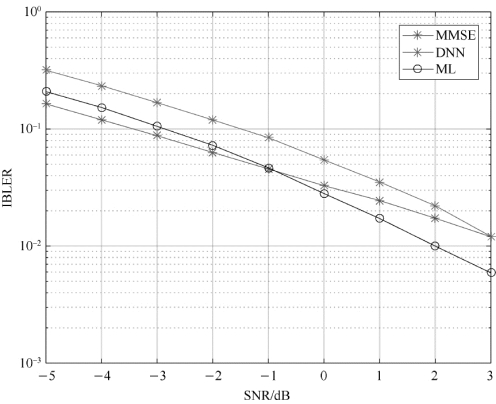
图8-9 coderate=0.1时的软检测性能
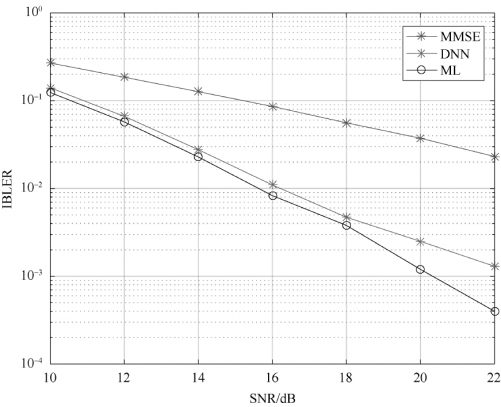
图8-10 coderate=0.8时的软检测性能
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




